6.1 Método de descenso más pronunciado para Unconstrained Convex Optimization (UCO)
Contents
6.1 Método de descenso más pronunciado para Unconstrained Convex Optimization (UCO)#
Notas para contenedor de docker:
Comando de docker para ejecución de la nota de forma local:
nota: cambiar <ruta a mi directorio> por la ruta de directorio que se desea mapear a /datos dentro del contenedor de docker y <versión imagen de docker> por la versión más actualizada que se presenta en la documentación.
docker run --rm -v <ruta a mi directorio>:/datos --name jupyterlab_optimizacion -p 8888:8888 -d palmoreck/jupyterlab_optimizacion_2:<versión imagen de docker>
password para jupyterlab: qwerty
Detener el contenedor de docker:
docker stop jupyterlab_optimizacion_2
Documentación de la imagen de docker palmoreck/jupyterlab_optimizacion_2:<versión imagen de docker> en liga.
Nota generada a partir de liga1
Al final de esta nota la comunidad lectora:
En esta nota se consideran problemas de optimización convexa sin restricciones, Unconstrained Convex Optimization (UCO):
con \(f_o:\mathbb{R}^n \rightarrow \mathbb{R}\) función objetivo fuertemente convexa y \(f_o \in \mathcal{C}^2(\text{dom}f_o)\).
Se asume que los puntos iniciales \(x^{(0)}\) de los métodos iterativos están en \(\text{dom}f_o\) y los conjuntos \(f_o(x^{(0)})\)-subnivel son conjuntos cerrados. También se asume que existe un punto óptimo \(x^*\) por lo que el problema tiene solución y el valor óptimo se denota por \(p^* = f_o(x^*) = \inf f_o(x)\)
Comentario
Las suposición que una función \(f\) sea convexa asegura que una condición necesaria y suficiente para que \(x^*\) sea óptimo es: \(\nabla f(x^*) = 0\) la cual es en general es un conjunto de \(n\) ecuaciones no lineales en \(n\) variables y que resuelve el problema de optimización planteado al inicio. Ver resultados útiles.
El método de steepest descent o descenso más pronunciado sigue los pasos del algoritmo ya revisado en método general de descenso para problemas UCO que a continuación nuevamente se describe.
Algoritmo: método general de descenso para problemas UCO#
Dado un punto inicial \(x\) en \(\text{dom}f_o\)
Repetir el siguiente bloque para \(k=0,1,2, \dots\)
Determinar una dirección de descenso \(\Delta x\).
Búsqueda de línea. Elegir un tamaño de paso \(t > 0\).
Hacer la actualización: \(x = x + t\Delta x\).
hasta convergencia (satisfacer criterio de paro).
Perspectiva del método de descenso más pronunciado#
Calcular una dirección \(\Delta x_{\text{nsd}}\) que satisfaga:
donde: \(||\cdot||\) es alguna norma en \(\mathbb{R}^n\).
Comentario
El subíndice “nsd” se refiere a normalized steepest descent.
Posteriormente con \(\Delta x_{\text{nsd}}\) se define el paso \(\Delta x_{\text{sd}}=||\nabla f_o(x)||_* \Delta x_{\text{nsd}}\) donde: \(|| \cdot||_*\) es la norma dual.
Definición
La norma dual asociada a \(||\cdot||\) se denota como \(||\cdot||_*\) y se define como:
Comentarios
Se puede probar que:
\(||z||_{2*}\) (la norma dual de la norma \(2\)) es \(||z||_2\) y \(||z||_{1*}\) (la norma dual de la norma \(1\)) es \(||z||_\infty\) \(\forall z \in \mathbb{R}^n\).
\(\Delta x_{\text{sd}}\) es dirección de descenso.
En la definición de \(\Delta x_{\text{nsd}}\) anterior:
Si \(||\cdot||\) es la norma \(2\): \(\Delta x_{\text{nsd}} = \text{argmin} \{ \nabla f_o(x)^Tv : ||v||_2 \leq 1, \nabla f_o(x)^Tv < 0 \} \) entonces
\[\Delta x_{\text{sd}} = - \nabla f_o(x).\]Lo cual prueba que el método de descenso más pronunciado generaliza al método de descenso en gradiente.
Si \(||\cdot||\) es una norma cuadrática con matriz \(P \in \mathbb{S}^n_{++}\): \(\Delta x_{\text{nsd}} = \text{argmin} \{ \nabla f_o(x)^Tv : ||v||_P \leq 1, \nabla f_o(x)^Tv < 0 \} \) entonces
\[\Delta x_{\text{sd}} = - P^{-1} \nabla f_o(x).\]Si \(P\) es la Hessiana de \(f_o\), \(P=\nabla ^2 f_o(x)\) tenemos el método de Newton por lo que es un caso particular del método de descenso más pronunciado. Si \(P=I\) tenemos el método de descenso en gradiente (punto anterior).
Si \(||\cdot||\) es la norma \(1\): \(\Delta x_{\text{nsd}} = \text{argmin} \{ \nabla f_o(x)^Tv : ||v||_1 \leq 1, \nabla f_o(x)^Tv < 0 \} \) entonces
\[\Delta x_{\text{sd}} = - \frac{\partial f_o(x)}{\partial x_i} e_i\]
con \(e_i\) \(i\)-ésimo vector canónico y el índice \(i\) es la entrada del vector \(\nabla f_o(x)\) de máxima magnitud: \(i\) tal que \(\left |(\nabla f_o(x))_i \right | = ||\nabla f_o(x)||_\infty\). En este caso el método se nombra coordinate descent, descenso por coordenadas. En cada iteración una única componente de \(x\) es actualizada.
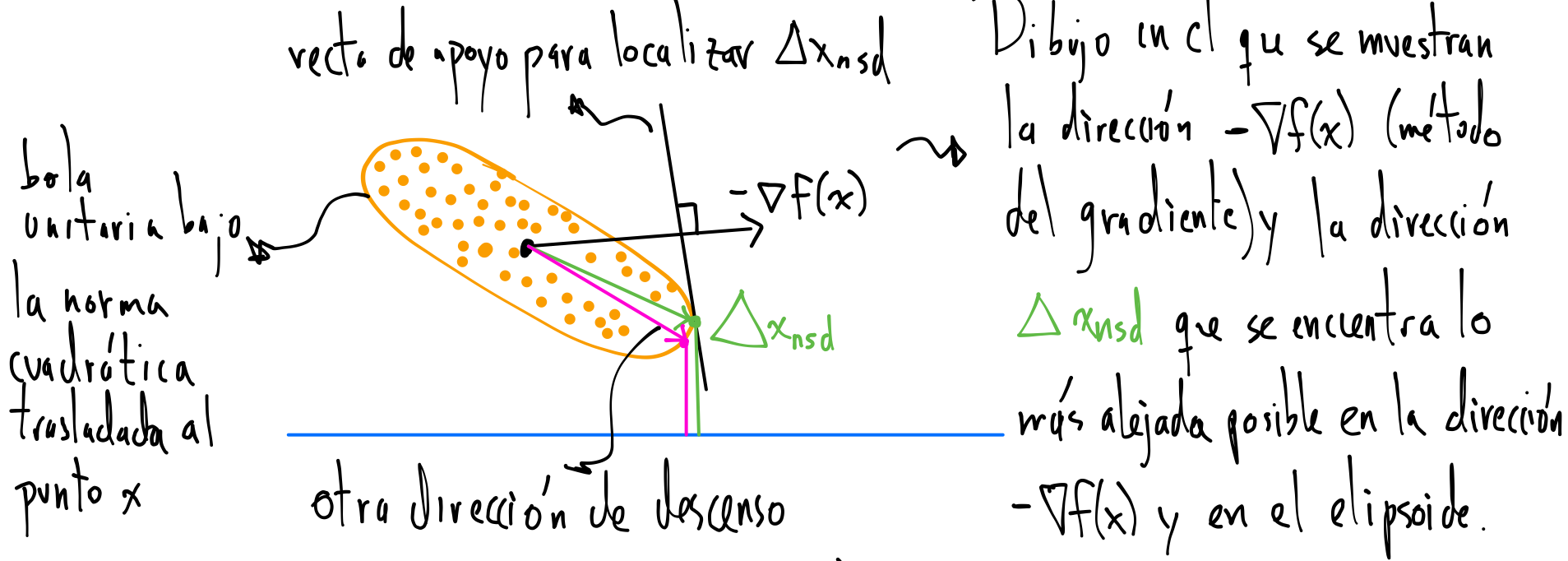
Interpretación: \(\Delta x_{\text{nsd}}\) es un paso tal que \(||\Delta x_{\text{nsd}}|| = 1\) y da el mayor decrecimiento en la aproximación lineal* de \(f_o\). Geométricamente es la dirección en la bola unitaria (generada por \(||\cdot||\)) que se extiende lo más lejos posible en la dirección \(-\nabla f_o(x)\).
*Recuérdese que la aproximación lineal a una función \(f_o\) está dada por Taylor a primer orden: \(f_o(x+v)=\hat{f}_o(x+v) = f_o(x) + \nabla f_o(x)^Tv\).
Para visualizar el paso \(\Delta x_{\text{nsd}}\) se tiene el siguiente dibujo:
Con la norma cuadrática:
Con la norma 1:

En los dibujos \(f = f_o\).
Ejemplos de los métodos de descenso en gradiente, Newton y descenso por coordenadas#
Algoritmo: Método de descenso en gradiente#
Dado un punto inicial \(x\) en \(\text{dom}f_o\)
Repetir el siguiente bloque para \(k=0,1,2,...\)
Calcular la dirección de descenso \(\Delta x = - \nabla f_o(x)\).
Búsqueda de línea. Elegir un tamaño de paso \(t > 0\).
Hacer la actualización: \(x = x + t\Delta x\).
hasta convergencia (satisfacer criterio de paro).
Algoritmo: Método de Newton#
Dado un punto inicial \(x\) en \(\text{dom}f_o\)
Repetir el siguiente bloque para \(k=0,1,2,\dots\)
Calcular la dirección de descenso de Newton \(\Delta x_{\text{nt}} = - \nabla ^2 f_o(x)^{-1} \nabla f_o(x)\) y el decremento de Newton al cuadrado: \(\lambda^2(x)=\nabla f_o(x)^T \nabla ^2 f_o(x)^{-1} \nabla f_o(x)\).
Búsqueda de línea. Elegir un tamaño de paso \(t > 0\) (usar el cálculo de \(\lambda (x)\) del paso anterior).
Hacer la actualización: \(x = x + t\Delta x_{\text{nt}}\).
hasta convergencia (satisfacer criterio de paro).
Algoritmo: Método de descenso por coordenadas#
Dado un punto inicial \(x\) en \(\text{dom}f_o\)
Repetir el siguiente bloque para \(k=0,1,2,\dots\)
Obtener el índice \(i\) de \(\nabla f_o(x)\) con máximo valor absoluto: \(\left |(\nabla f_o(x))_i \right | = ||\nabla f_o(x)||_\infty\).
Calcular la dirección de descenso más pronunciado bajo la norma \(1\): \(\Delta x_{\text{sd}} = - \frac{\partial f_o(x)}{\partial x_i} e_i\) con \(e_i\) \(i\)-ésimo vector canónico.
Búsqueda de línea. Elegir un tamaño de paso \(t > 0\).
Hacer la actualización: \(x = x + t\Delta x\).
hasta convergencia (satisfacer criterio de paro).
Definición
En el algoritmo anterior se utilizó \(\lambda(x)\), ver decremento de Newton.
import numpy as np
import sympy
import math
from sympy.tensor.array import derive_by_array
import matplotlib.pyplot as plt
from opt.classes.problems import ProblemFeasibleInitPoint
from opt.classes.functions import GradientObjectiveFunction, HessianObjectiveFunction
type_problem = "UCO"
fo_numpy = lambda x: (x[0]-2)**2 + (2-x[1])**2 + x[2]**2 + x[3]**4
p = ProblemFeasibleInitPoint(type_problem,
fo_numpy)
if p.well_defined_problem:
print("problema %s bien definido" % p.type_problem)
else:
print("problema %s no bien definido" % p.type_problem)
problema UCO bien definido
def map_sympy_vars_to_array_values(x):
"""
Args:
x (numpy ndarray): 1d array of floats
"""
n = x.size
return {"x%s" % i: x[i-1] for i in range(1,n+1)}
x1, x2, x3, x4 = sympy.symbols("x1, x2, x3, x4")
x_sympy = (x1, x2, x3, x4)
fo_sympy = (x1 - 2)**2 + (2 - x2)**2 + x3**2 + x4**2
gf_sympy = derive_by_array(fo_sympy, x_sympy)
Hf_sympy = derive_by_array(gf_sympy, x_sympy)
n = len(x_sympy)
gf = lambda x: np.array([first_partial_derivative.subs(map_sympy_vars_to_array_values(x)) \
for first_partial_derivative in gf_sympy],
dtype = float)
Hf = lambda x: np.array([second_partial_derivative.subs(map_sympy_vars_to_array_values(x)) \
for second_partial_derivative in Hf_sympy],
dtype=float).reshape(n,n)
gf_class = GradientObjectiveFunction(gf)
Hf_class = HessianObjectiveFunction(Hf)
x_ast = np.array([2,2,0,0],dtype=float)
p_ast = fo_numpy(x_ast)
x_0 = np.array([5,5,1,0],dtype=float)
[x,iteration,Err_plot,x_plot] = p.solve(x_0,
x_ast=x_ast,
p_ast=p_ast,
gf_B=gf_class,
Hf_B=Hf_class,
plot=False
)
will use Newton's method, if wants to use another select gradient or coordinate descent
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | CondHf | |
|---|---|---|---|---|---|---|---|
| row0 | 0 | 8.72e+00 | 3.80e+01 | 1.54e+00 | 1.90e+01 | --- | 1.00e+00 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | CondHf | |
|---|---|---|---|---|---|---|---|
| row1 | 1 | 0.00e+00 | 0.00e+00 | 0.00e+00 | 0.00e+00 | 1 | 1.00e+00 |
Error of x with respect to x_ast: 0.00e+00
Approximate solution: [2. 2. 0. 0.]
[x,iteration,Err_plot,x_plot] = p.solve(x_0,
x_ast=x_ast,
p_ast=p_ast,
gf_B=gf_class,
Hf_B=Hf_class,
plot=False,
method="gradient"
)
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row0 | 0 | 8.72e+00 | 7.60e+01 | 1.54e+00 | 1.90e+01 | --- |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row1 | 1 | 0.00e+00 | 0.00e+00 | 0.00e+00 | 0.00e+00 | 5.00e-01 |
Error of x with respect to x_ast: 0.00e+00
Approximate solution: [2. 2. 0. 0.]
[x,iteration,Err_plot,x_plot] = p.solve(x_0,
x_ast=x_ast,
p_ast=p_ast,
gf_B=gf_class,
Hf_B=Hf_class,
plot=False,
method="coordinate descent"
)
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row0 | 0 | 8.72e+00 | 3.60e+01 | 1.54e+00 | 1.90e+01 | --- |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row1 | 1 | 6.32e+00 | 3.60e+01 | 1.12e+00 | 1.00e+01 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row2 | 2 | 2.00e+00 | 4.00e+00 | 3.54e-01 | 1.00e+00 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row3 | 3 | 0.00e+00 | 0.00e+00 | 0.00e+00 | 0.00e+00 | 5.00e-01 |
Error of x with respect to x_ast: 0.00e+00
Approximate solution: [2. 2. 0. 0.]
type_problem = "UCO"
fo_numpy = lambda x: math.exp(x[0]+3*x[1]-0.1)+math.exp(x[0]-3*x[1]-0.1)+math.exp(-x[0]-0.1)
p = ProblemFeasibleInitPoint(type_problem,
fo_numpy)
if p.well_defined_problem:
print("problema %s bien definido" % p.type_problem)
else:
print("problema %s no bien definido" % p.type_problem)
problema UCO bien definido
x1, x2 = sympy.symbols("x1, x2")
x_sympy = (x1, x2)
fo_sympy = sympy.exp(x1+3*x2-0.1) + sympy.exp(x1-3*x2-0.1) + sympy.exp(-x1-0.1)
gf_sympy = derive_by_array(fo_sympy, x_sympy)
Hf_sympy = derive_by_array(gf_sympy, x_sympy)
n = len(x_sympy)
gf = lambda x: np.array([first_partial_derivative.subs(map_sympy_vars_to_array_values(x)) \
for first_partial_derivative in gf_sympy],
dtype = float)
Hf = lambda x: np.array([second_partial_derivative.subs(map_sympy_vars_to_array_values(x)) \
for second_partial_derivative in Hf_sympy],
dtype=float).reshape(n,n)
gf_class = GradientObjectiveFunction(gf)
Hf_class = HessianObjectiveFunction(Hf)
x_ast=np.array([-0.3465735941251887,0], dtype=float)
p_ast=fo_numpy(x_ast)
x_0 = np.array([0,0],dtype=float)
[x,iteration,Err_plot,x_plot] = p.solve(x_0,
x_ast=x_ast,
p_ast=p_ast,
gf_B=gf_class,
Hf_B=Hf_class
)
will use Newton's method, if wants to use another select gradient or coordinate descent
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | CondHf | |
|---|---|---|---|---|---|---|---|
| row0 | 0 | 9.05e-01 | 3.02e-01 | 1.00e+00 | 6.07e-02 | --- | 6.00e+00 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | CondHf | |
|---|---|---|---|---|---|---|---|
| row1 | 1 | 3.39e-02 | 4.49e-04 | 3.82e-02 | 8.77e-05 | 1 | 4.56e+00 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | CondHf | |
|---|---|---|---|---|---|---|---|
| row2 | 2 | 1.98e-06 | 1.53e-12 | 2.24e-06 | 2.99e-13 | 1 | 4.50e+00 |
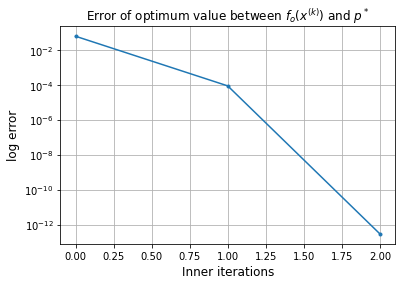
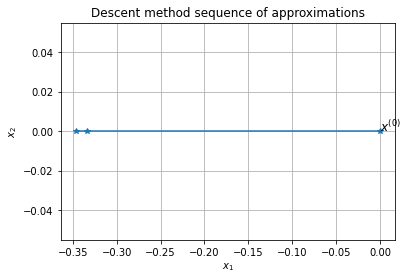
Error of x with respect to x_ast: 2.24e-06
Approximate solution: [-0.34657282 0. ]
[x,iteration,Err_plot,x_plot] = p.solve(x_0,
x_ast=x_ast,
p_ast=p_ast,
gf_B=gf_class,
Hf_B=Hf_class,
method="gradient"
)
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row0 | 0 | 9.05e-01 | 8.19e-01 | 1.00e+00 | 6.07e-02 | --- |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row1 | 1 | 2.71e-01 | 7.37e-02 | 3.05e-01 | 5.61e-03 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row2 | 2 | 7.64e-02 | 5.84e-03 | 8.61e-02 | 4.46e-04 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row3 | 3 | 2.14e-02 | 4.57e-04 | 2.41e-02 | 3.49e-05 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row4 | 4 | 5.98e-03 | 3.57e-05 | 6.74e-03 | 2.73e-06 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row5 | 5 | 1.67e-03 | 2.79e-06 | 1.88e-03 | 2.13e-07 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row6 | 6 | 4.67e-04 | 2.19e-07 | 5.27e-04 | 1.67e-08 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row7 | 7 | 1.31e-04 | 1.71e-08 | 1.47e-04 | 1.30e-09 | 5.00e-01 |
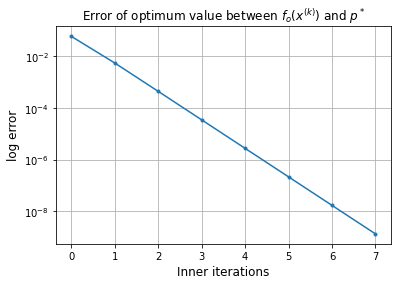
Error of x with respect to x_ast: 1.47e-04
Approximate solution: [-0.34662467 0. ]
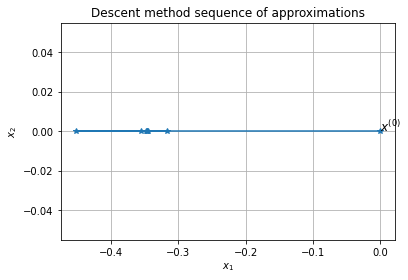
[x,iteration,Err_plot,x_plot] = p.solve(x_0,
x_ast=x_ast,
p_ast=p_ast,
gf_B=gf_class,
Hf_B=Hf_class,
method="coordinate descent"
)
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row0 | 0 | 9.05e-01 | 8.19e-01 | 1.00e+00 | 6.07e-02 | --- |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row1 | 1 | 2.71e-01 | 7.37e-02 | 3.05e-01 | 5.61e-03 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row2 | 2 | 7.64e-02 | 5.84e-03 | 8.61e-02 | 4.46e-04 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row3 | 3 | 2.14e-02 | 4.57e-04 | 2.41e-02 | 3.49e-05 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row4 | 4 | 5.98e-03 | 3.57e-05 | 6.74e-03 | 2.73e-06 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row5 | 5 | 1.67e-03 | 2.79e-06 | 1.88e-03 | 2.13e-07 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row6 | 6 | 4.67e-04 | 2.19e-07 | 5.27e-04 | 1.67e-08 | 5.00e-01 |
| Iter | Normgf | Newtons decrement | Err x ast | Err p ast | line search | |
|---|---|---|---|---|---|---|
| row7 | 7 | 1.31e-04 | 1.71e-08 | 1.47e-04 | 1.30e-09 | 5.00e-01 |
Error of x with respect to x_ast: 1.47e-04
Approximate solution: [-0.34662467 0. ]
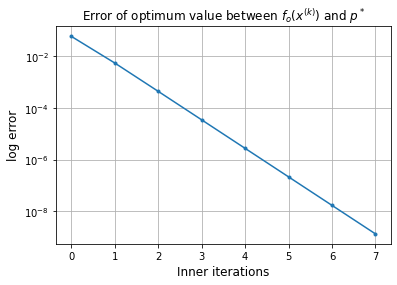
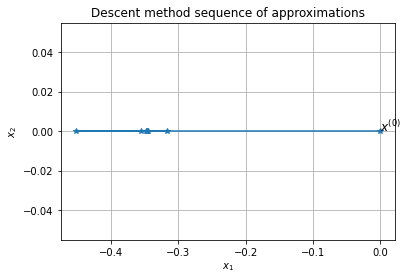
Ejemplos del método de descenso más pronunciado bajo la norma cuadrática como caso particular del método de descenso en gradiente#
Definición
Sea \(P \in \mathbb{S}^n_+\), \(P^{1/2}\) se nombra raíz cuadrada simétrica, symmetric squareroot y se define como
con \(Q\) y \(diag(\lambda_1^{1/2},\dots,\lambda_n^{1/2})\) obtenidas con la descomposición espectral de \(P\).
Es posible probar que el método de descenso más pronunciado bajo la norma cuadrática \(||\cdot||_P\) es el método de descenso en gradiente aplicado al problema de optimización después del cambio de coordenadas \(\hat{x}=P^{1/2}x\). En este cambio de coordenadas \(x\) es la variable original por lo que si deseamos utilizar descenso en gradiente utilizamos la inversa de la matriz raíz cuadrada simétrica \(P^{1/2}\) quedando la transformación como: \(x = P^{-1/2}\hat{x}\).
Ejemplos
De la nota descenso en gradiente_Python
- \[\min \quad (x_1-2)^2+(2-x_2)^2+x_3^2+x_4^4\]
El método de descenso en gradiente es altamente sensible a la forma de las curvas de nivel de la función objetivo \(f_o\). Para observar esto considérese el problema: $\(\min \frac{1}{2}\left(x_1^2+Cx_2^2 \right)\)$
- \[\min \quad e^{(x_1+3x_2-0.1)}+e^{x_1-3x_2-0.1}+e^{-x_1-0.1}\]
Comentarios:
Como se observa en los ejemplos anteriores la elección de la norma en el método de descenso más pronunciado tiene un efecto fuerte en la tasa de convergencia.
Siempre existe una matriz \(P\) para la cual el método de descenso más pronunciado tiene una convergencia buena. El reto está en encontrar tal matriz. La idea es identificar una matriz \(P\) para la cual el problema transformado tenga un número de condición moderado.
De la nota descenso por coordenadas
- \[\min \quad (x_1-2)^2+(2-x_2)^2+x_3^2+x_4^4\]
- \[\min \frac{1}{2}\left(x_1^2+Cx_2^2 \right)\]
- \[\min \quad e^{(x_1+3x_2-0.1)}+e^{x_1-3x_2-0.1}+e^{-x_1-0.1}\]
De la nota Método Newton Python
- \[\min \quad e^{(x_1+3x_2-0.1)}+e^{x_1-3x_2-0.1}+e^{-x_1-0.1}\]
El método de Newton es insensible a la forma de las curvas de nivel de la función objetivo \(f_o\). Para observar esto considérese el problema:
Ejercicios
1.Resuelve los ejercicios y preguntas de la nota.
Preguntas de comprehensión
Referencias:
S. P. Boyd, L. Vandenberghe, Convex Optimization, Cambridge University Press, 2009.

