1.3 Normas vectoriales y matriciales

Notas para contenedor de docker:

Comando de docker para ejecución de la nota de forma local:

nota: cambiar <ruta a mi directorio> por la ruta de directorio que se desea mapear a /datos dentro del contenedor de docker y <versión imagen de docker> por la versión más actualizada que se presenta en la documentación.

docker run --rm -v <ruta a mi directorio>:/datos --name jupyterlab_optimizacion -p 8888:8888 -d palmoreck/jupyterlab_optimizacion:<versión imagen de docker>

password para jupyterlab: qwerty

Detener el contenedor de docker:

docker stop jupyterlab_optimizacion

Documentación de la imagen de docker palmoreck/jupyterlab_optimizacion:<versión imagen de docker> en liga.

---

Nota generada a partir de liga

Al final de esta nota la comunidad lectora:

• Aprenderá las definiciones de algunas normas vectoriales y matriciales más utilizadas en las Matemáticas para la medición de errores, residuales, en general cercanía a cantidades de interés.

• Comprenderá la interpretación que tiene una norma matricial.

Una norma define una medida de distancia en un conjunto y da nociones de tamaño, vecindad, convergencia y continuidad.

Normas vectoriales

Sea \(\mathbb{R}^n\) el conjunto de \(n\)-tuplas o vectores columna o \(1\)-arreglo de orden \(1\), esto es:

\[\begin{split}x \in \mathbb{R}^n \iff x = \left[\begin{array}{c} x_1\\ x_2\\ \vdots\\ x_n \end{array} \right] \text{ con } x_i \in \mathbb{R}\end{split}\]

Una norma vectorial en \(\mathbb{R}^n\) es una función \(g: \mathbb{R}^n \rightarrow \mathbb{R}\) que satisface las siguientes propiedades:

• \(g\) es no negativa: \(g(x) \geq 0 \forall x \in \mathbb{R}^n\).

• \(g\) es definida: \(g(x) = 0 \iff x = 0\).

• \(g\) satisface la desigualdad del triángulo:

\[g(x+y) \leq g(x) + g(y) \forall x,y \in \mathbb{R}^n.\]

• \(g\) es homogénea: \(g(\alpha x)=|\alpha|g(x), \forall \alpha \in \mathbb{R}, \forall x \in \mathbb{R}^n\).

Notación: \(g(x) = ||x||\).

Definición

Un conjunto \(V \neq \emptyset\) en el que se le han definido las operaciones \((+, \cdot)\) se le nombra espacio vectorial sobre \(\mathbb{R}\) si satisface las siguientes propiedades \(\forall x, y, z \in V\), \(\forall a,b \in \mathbb{R}\):

• x + (y + z) = (x + y) + z

• x + y = y + x

• \(\exists 0 \in V\) tal que \(x + 0 = 0 + x = x\) \(\forall x \in V\).

• \(\forall x \in V\) \(\exists -x \in V\) tal que \(x + (-x) = 0\).

• a(bx) = (ab)x.

• \(1x = x\) con \(1 \in \mathbb{R}\).

• \(a(x + y) = ax + ay\).

• \((a+b)x = ax + bx\).

Comentarios y propiedades

• Una norma es una generalización del valor absoluto de \(\mathbb{R}\): \(|x|, x \in \mathbb{R}.\)

• Un espacio vectorial con una norma definida en éste se le llama espacio vectorial normado.

• Una norma es una medida de la longitud de un vector.

• Con una norma es posible definir conceptos como distancia entre vectores: \(x,y \in \mathbb{R}^n: \text{dist}(x,y) = ||x-y||\).

• Existen varias normas en \(\mathbb{R}^n\) siendo las más comunes:

• La norma \(\mathcal{l}_2\), Euclidiana o norma \(2\): \(||x||_2\).

• La norma \(\mathcal{l}_1\) o norma \(1\): \(||x||_1\).

• La norma \(\infty\) o de Chebyshev o norma infinito: \(||x||_\infty\).

Las normas anteriores pertenecen a una familia parametrizada por una constante \(p, p \geq 1\) cuyo nombre es norma \(\mathcal{l}_p\):

\[ ||x||_p = \left(\displaystyle \sum_{i=1}^n|x_i|^p \right )^{1/p}.\]

• Un resultado para \(x \in \mathbb{R}^n\) es la equivalencia entre normas:

\[\exists \alpha, \beta > 0 \text{ tales que }: \alpha||x||_a \leq ||x||_b \leq \beta ||x||_a \forall x \in \mathbb{R}^n\]

donde: \(||\cdot||_a, ||\cdot||_b\) son normas cualesquiera en \(\mathbb{R}^n\). Por la propiedad anterior decimos que si se cumple convergencia en la norma \(||\cdot||_a\) entonces también se cumple convergencia en la norma \(||\cdot||_b\).

Ejemplos de gráficas de normas en el plano.

import numpy as np
import matplotlib.pyplot as plt

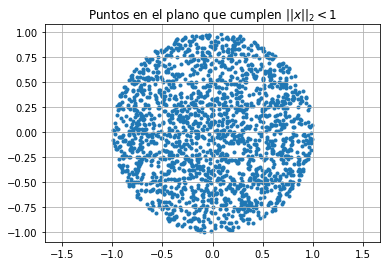
Norma \(2\): \(\{ x \in \mathbb{R}^2 \text{ tales que } ||x||_2 < 1\}\)

f=lambda x: np.sqrt(x[:,0]**2 + x[:,1]**2) #definición de norma2
density=1e-5
density_p=int(2.5*10**3)
x=np.arange(-1,1,density)
y1=np.sqrt(1-x**2)
y2=-np.sqrt(1-x**2)
x_p=np.random.uniform(-1,1,(density_p,2))
ind=f(x_p)<1
x_p_subset=x_p[ind]
plt.scatter(x_p_subset[:,0],x_p_subset[:,1],marker='.')
plt.title('Puntos en el plano que cumplen $||x||_2 < 1$')
plt.grid()
plt.axis("equal")
plt.show()

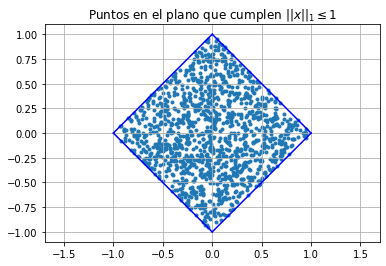
Norma \(1\): \(\{ x \in \mathbb{R}^2 \text{ tales que } ||x||_1 \leq 1\}\)

f=lambda x:np.abs(x[:,0]) + np.abs(x[:,1]) #definición de norma1
density=1e-5
density_p=int(2.5*10**3)
x1=np.arange(0,1,density)
x2=np.arange(-1,0,density)
y1=1-x1
y2=1+x2
y3=x1-1
y4=-1-x2
x_p=np.random.uniform(-1,1,(density_p,2))
ind=f(x_p)<=1
x_p_subset=x_p[ind]
plt.plot(x1,y1,'b',x2,y2,'b',x1,y3,'b',x2,y4,'b')
plt.scatter(x_p_subset[:,0],x_p_subset[:,1],marker='.')
plt.title('Puntos en el plano que cumplen $||x||_1 \leq 1$')
plt.grid()
plt.axis("equal")
plt.show()

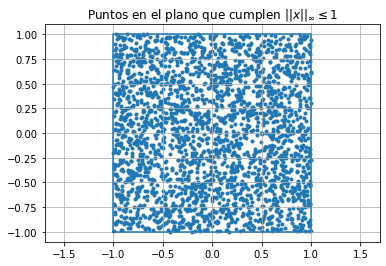
Norma \(\infty\): \(\{ x \in \mathbb{R}^2 \text{ tales que } ||x||_\infty \leq 1\}\)

f=lambda x:np.max(np.abs(x),axis=1) #definición de norma infinito
point1 = (-1, -1)
point2 = (-1, 1)
point3 = (1, 1)
point4 = (1, -1)
point5 = point1
arr = np.row_stack((point1, point2,
                    point3, point4,
                    point5))
density_p=int(2.5*10**3)
x_p=np.random.uniform(-1,1,(density_p,2))
ind=f(x_p)<=1
x_p_subset=x_p[ind]
plt.scatter(x_p_subset[:,0],x_p_subset[:,1],marker='.')
plt.plot(arr[:,0], arr[:,1])
plt.title('Puntos en el plano que cumplen $||x||_{\infty} \leq 1$')
plt.grid()
plt.axis("equal")
plt.show()

Observación

La norma \(\infty\) se encuentra en la familia de las normas-p como límite:

\[||x||_\infty = \displaystyle \lim_{p \rightarrow \infty} ||x||_p.\]

Comentario

En la norma \(\mathcal{l}_2\) o Euclidiana \(||x||_2\) tenemos una desigualdad muy importante, la desigualdad de Cauchy-Schwartz:

\[|x^Ty| \leq ||x||_2||y||_2 \forall x,y \in \mathbb{R}^n\]

la cual relaciona el producto interno estándar para \(x,y \in \mathbb{R}^n\): \(<x,y> = x^Ty = \displaystyle \sum_{i=1}^nx_iy_i\) con la norma \(\mathcal{l}_2\) de \(x\) y la norma \(\mathcal{l}_2\) de \(y\). Además se utiliza lo anterior para definir el ángulo (sin signo por el intervalo en el que está \(\cos^{-1}\)) entre \(x,y\):

\[\measuredangle x,y = \cos ^{-1}\left(\frac{x^Ty}{||x||_2||y||_2} \right )\]

para \(\cos^{-1}(u) \in [0,\pi]\) y se nombra a \(x,y\) ortogonales si \(x^Ty=0\). Obsérvese que \(||x||_2 = \sqrt{x^Tx}\).

Ejemplo

También se utilizan matrices para definir normas.

Definición

Recuérdese que una matriz es un arreglo \(2\)-dimensional de datos o \(2\) arreglo de orden \(2\). Se utiliza la notación \(A \in \mathbb{R}^{m\times n}\) para denotar:

\[\begin{split}A = \left[\begin{array}{cccc} a_{11} &a_{12}&\dots&a_{1n}\\ a_{21} &a_{22}&\dots&a_{2n}\\ \vdots &\vdots& \vdots&\vdots\\ a_{n1} &a_{n2}&\dots&a_{nn}\\ \vdots &\vdots& \vdots&\vdots\\ a_{m-11} &a_{m-12}&\dots&a_{m-1n}\\ a_{m1} &a_{m2}&\dots&a_{mn} \end{array} \right] \end{split}\]

con \(a_{ij} \mathbb{R} \forall i=1,\dots,m, j=1,\dots,n\). Y se utilizan las siguientes notaciones para describir a la matriz \(A\):

• \(A=(a_1,\dots a_n), a_j \in \mathbb{R}^m (=\mathbb{R}^{m\times1}) \forall j=1,\dots,n\).

• \(A=\left ( \begin{array}{c} a_1^T\\ \vdots\\ a_m^T \end{array} \right ), a_i \in \mathbb{R}^n (=\mathbb{R}^{n\times1}) \forall i=1,\dots,m\).

La multiplicación de una matriz de tamaño \(m\times n\) por un vector se define como:

\[y=Ax=\displaystyle \sum_{j=1}^n a_jx_j\]

con \(a_j \in \mathbb{R}^m, x \in \mathbb{R}^n\). Obsérvese que \(x \in \mathbb{R}^n, Ax \in \mathbb{R}^m\).

Un ejemplo de norma-\(2\) ponderada es: \(\{x \in \mathbb{R}^2 \text{ tales que } ||x||_D \leq 1, ||x||_D = ||Dx||_2, \text{con matriz diagonal } D \text{ y entradas positivas}\}\):

d1_inv=1/5
d2_inv=1/3
f=lambda x: np.sqrt((d1_inv*x[:,0])**2 + (d2_inv*x[:,1])**2) #definición de norma2
density=1e-5
density_p=int(2.5*10**3)
x=np.arange(-1/d1_inv,1/d1_inv,density)
y1=1.0/d2_inv*np.sqrt(1-(d1_inv*x)**2)
y2=-1.0/d2_inv*np.sqrt(1-(d1_inv*x)**2)
x_p=np.random.uniform(-1/d1_inv,1/d1_inv,(density_p,2))
ind=f(x_p)<=1
x_p_subset=x_p[ind]
plt.plot(x,y1,'b',x,y2,'b')
plt.scatter(x_p_subset[:,0],x_p_subset[:,1],marker='.')
plt.title('Puntos en el plano que cumplen $||x||_D \leq 1$')
plt.grid()
plt.axis("equal")
plt.show()

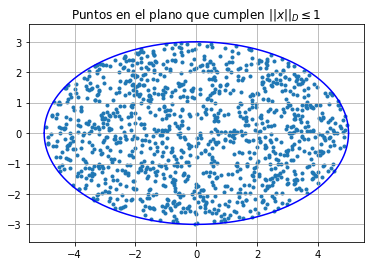
en este caso \(D=\left[\begin{array}{cc} \frac{1}{25} &0\\ 0 &\frac{1}{9} \end{array}\right ] = \left[\begin{array}{cc} \frac{1}{d_1} &0\\ 0 &\frac{1}{d_2} \end{array}\right ]\)

Definiciones

• Una matriz \(A\) es simétrica si \(A = A^T\), con \(A^T\) la transpuesta de \(A\).

• Una matriz \(A\) es semidefinida positiva si \(x^TAx \geq 0, \forall x \in \mathbb{R}^n - \{0\}\). Si se cumple de forma estricta la desigualdad entonces \(A\) es definida positiva.

• La norma cuadrática de \(z\) con matriz \(A\) se define como \(||z||_A = \sqrt{z^TAz}\) con \(A\) matriz simétrica definida positiva.

Normas matriciales

Inducidas

De las normas matriciales más importantes se encuentran las inducidas por normas vectoriales. Estas normas matriciales se definen en términos de los vectores en \(\mathbb{R}^n\) a los que se les aplica la multiplicación \(Ax\):

Dadas las normas vectoriales \(||\cdot||_{(n)}, ||\cdot||_{(m)}\) en \(\mathbb{R}^n\) y \(\mathbb{R}^m\) respectivamente, la norma matricial inducida \(||A||_{(m,n)}\) para \(A \in \mathbb{R}^{m \times n}\) es el menor número \(C\) para el cual la desigualdad:

\[||Ax||_{(m)} \leq C||x||_{(n)}\]

se cumple \(\forall x \in \mathbb{R}^n\). Esto es:

\[||A||_{(m,n)} = \displaystyle \sup_{x \in \mathbb{R}^n-\{0\}} \frac{||Ax||_{(m)}}{||x||_{(n)}}\]

Ver Nota sobre sup e inf para definición de \(\sup\).

Comentarios

• \(||A||_{(m,n)}\) representa el máximo factor por el cual \(A\) puede modificar el tamaño de \(x\) sobre todos los vectores \(x \in \mathbb{R}^n\), es una medida de un tipo de worst case stretch factor.

• Así definidas, la norma \(||\cdot||_{(m,n)}\) es la norma matricial inducida por las normas vectoriales \(||\cdot||_{(m)}, ||\cdot||_{(n)}\).

• Son definiciones equivalentes:

\[||A||_{(m,n)} = \displaystyle \sup_{x \in \mathbb{R}^n-\{0\}} \frac{||Ax||_{(m)}}{||x||_{(n)}} = \displaystyle \sup_{||x||_{(n)} \leq 1} \frac{||Ax||_{(m)}}{||x||_{(n)}} = \displaystyle \sup_{||x||_{(n)}=1} ||Ax||_{(m)}\]

Ejemplo

La matriz \(A=\left[\begin{array}{cc} 1 &2\\ 0 &2 \end{array}\right ]\) mapea \(\mathbb{R}^2\) a \(\mathbb{R}^2\), en particular se tiene:

• \(A\) mapea \(e_1 = \left[\begin{array}{c} 1 \\ 0 \end{array}\right ]\) a la columna \(a_1 = \left[\begin{array}{c} 1 \\ 0 \end{array}\right ]\) de \(A\).

• \(A\) mapea \(e_2 = \left[\begin{array}{c} 0 \\ 1 \end{array}\right ]\) a la columna \(a_2 = \left[\begin{array}{c} 2 \\ 2 \end{array}\right ]\) de \(A\).

Considerando \(||A||_p := ||A||_{(p,p)}\) con \(p=1, p=2, p=\infty\) se tiene:

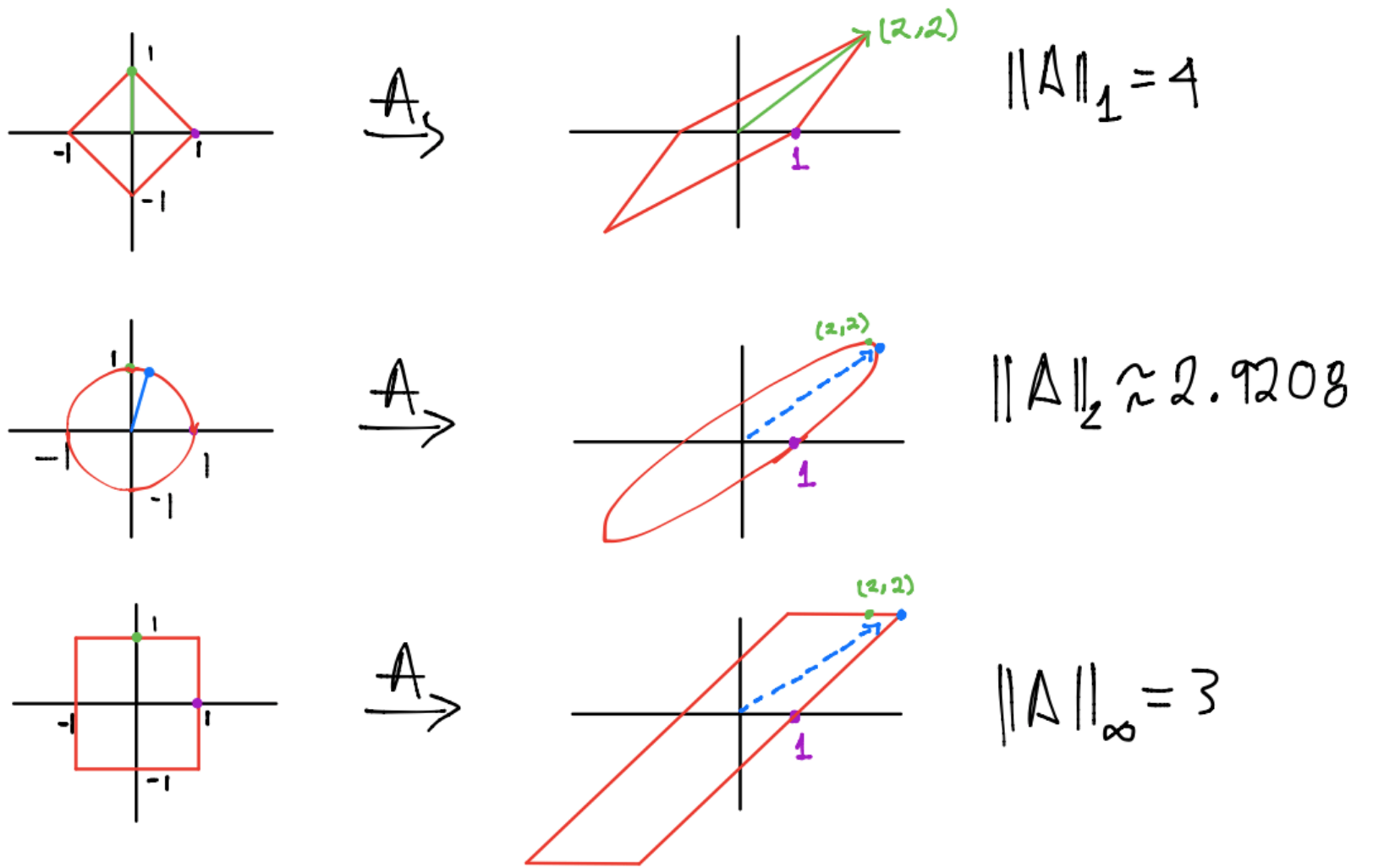
Observación

Al observar la segunda gráfica se tiene la siguiente afirmación: la acción de una matriz sobre una circunferencia es una elipse con longitudes de semiejes iguales a \(|d_i|\). En general la acción de una matriz sobre una hiper esfera es una hiperelipse. Por lo que los vectores unitarios en \(\mathbb{R}^n\) que son más amplificados por la acción de una matriz diagonal \(D \in \mathbb{R}^{m\times n}\) con entradas iguales a \(d_i\) son aquellos que se mapean a los semiejes de una hiperelipse en \(\mathbb{R}^m\) de longitud igual a \(\max\{|d_i|\}\) y así tenemos: si \(D\) es una matriz diagonal con entradas \(d_i\) entonces \(||D||_2 = \displaystyle \max_{i=1,\dots,m}\{|d_i|\}\).

Ejemplo

A=np.array([[1,2],[0,2]])
density=1e-5
x1=np.arange(0,1,density)
x2=np.arange(-1,0,density)
x1_y1 = np.column_stack((x1,1-x1))
x2_y2 = np.column_stack((x2,1+x2))
x1_y3 = np.column_stack((x1,x1-1))
x2_y4 = np.column_stack((x2,-1-x2))
apply_A = lambda vec : np.transpose(A@np.transpose(vec))
A_to_vector_1 = apply_A(x1_y1)
A_to_vector_2 = apply_A(x2_y2)
A_to_vector_3 = apply_A(x1_y3)
A_to_vector_4 = apply_A(x2_y4)
plt.subplot(1,2,1)
plt.plot(x1_y1[:,0],x1_y1[:,1],'b',
         x2_y2[:,0],x2_y2[:,1],'b',
         x1_y3[:,0],x1_y3[:,1],'b',
         x2_y4[:,0],x2_y4[:,1],'b')
e1 = np.array([[0,0],
               [1, 0]])
e2 = np.array([[0, 0],
               [0, 1]])
plt.plot(e2[:,0], e2[:,1],'g',
         e1[:,0], e1[:,1],'b')
plt.xlabel('Vectores con norma 1 menor o igual a 1')
plt.grid()
plt.axis("equal")
plt.subplot(1,2,2)
plt.plot(A_to_vector_1[:,0],A_to_vector_1[:,1],'b',
         A_to_vector_2[:,0],A_to_vector_2[:,1],'b',
         A_to_vector_3[:,0],A_to_vector_3[:,1],'b',
         A_to_vector_4[:,0],A_to_vector_4[:,1],'b')
A_to_vector_e2 = apply_A(e2)
plt.plot(A_to_vector_e2[:,0],A_to_vector_e2[:,1],'g')
plt.grid()
plt.axis("equal")
plt.title('Efecto de la matriz A sobre los vectores con norma 1 menor o igual a 1')
plt.show()

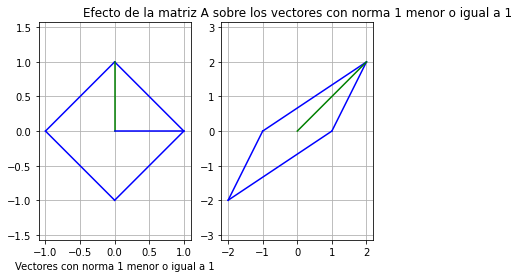
print(np.linalg.norm(A,1))

4.0

Ejercicio

Utilizando lenguajes de programación obtener las otras dos gráficas usando norma \(2\) y norma \(\infty\). Para el caso de la norma \(2\) el vector en color azul está dado por la descomposición en valores singulares (SVD) de A. En específico la primer columna de la matriz \(U\) multiplicado por el primer valor singular. En el ejemplo resulta en:

\[\begin{split}\sigma_1U[:,0] \approx 2.9208*\left[ \begin{array}{c} 0.74967 \\ 0.66180 \end{array} \right] \approx \left[\begin{array}{c} 2.189\\ 1.932 \end{array} \right] \end{split}\]

y el vector \(v\) que será multiplicado por la matriz \(A\) es la primer columna de \(V\) dada por:

\[\begin{split}V[:,0] \approx \left[ \begin{array}{c} 0.2566\\ 0.9664 \end{array} \right] \end{split}\]

Resultados computacionales que son posibles probar

1.\(||A||_1 = \displaystyle \max_{j=1,\dots,n}\sum_{i=1}^n|a_{ij}|\).

2.\(||A||_\infty = \displaystyle \max_{i=1,\dots,n}\sum_{j=1}^n|a_{ij}|\).

3.\(\begin{eqnarray}||A||_2 = \sqrt{\lambda_{\text{max}}(A^TA)} &=& \max \left \{\sqrt{\lambda}\in \mathbb{R} | \lambda \text{ es eigenvalor de } A^TA \right \} \nonumber \\ &=& \max \left \{ \sigma \in \mathbb{R} | \sigma \text{ es valor singular de A } \right \} \nonumber \\ &=& \sigma_{\text{max}}(A) \end{eqnarray}\).

por ejemplo para la matriz anterior se tiene:

print(np.linalg.norm(A,2))

2.9208096264818897

_,s,_ = np.linalg.svd(A)
print(np.max(s))

2.9208096264818897

Otras normas matriciales

• Norma de Frobenius: \(||A||_F = \text{tr}(A^TA)^{1/2} = \left ( \displaystyle \sum_{i=1}^m \sum_{j=1}^n a_{ij}^2 \right ) ^{1/2}\).

• Norma “sum-absolute-value”: \(||A||_{sav} = \displaystyle \sum_{i=1}^m \sum_{j=1}^n |a_{ij}|\).

• Norma “max-absolute-value”: \(||A||_{mav} = \displaystyle \max \left\{|a_{ij}| \text{ para } i=1,\dots,m , j=1,\dots,n \right \}\).

Comentarios

• El producto interno estándar en \(\mathbb{R}^{m\times n}\) es: \(<A,B> = tr(A^TB) = \displaystyle \sum_{i=1}^m \sum_{j=1}^n a_{ij}b_{ij}\).

• La norma \(2\) (también llamada norma espectral o \(\mathcal{l}_2\)) y la norma de Frobenius cumplen la propiedad de consistencia:

\[||Ax|| \leq ||A|| ||x|| \forall x \in \mathbb{R}^n, \forall A \in \mathbb{R}^{m\times n}.\]

\[||AB|| \leq ||A|| ||B|| \forall A,B \text{ matrices con dimensiones correspondientes para su multiplicación}.\]

Observación

La propiedad de consistencia también es cumplida por las normas-\(p\) matriciales.

---

Nota sobre \(\sup\) e \(\inf\)

Si \(C \subseteq \mathbb{R}\) entonces \(a \subseteq \mathbb{R}\) es una cota superior en \(C\) si

\[ x \leq a, \forall x \in C.\]

En \(\mathbb{R}\) el conjunto de cotas superiores es \(\emptyset, \mathbb{R}\) ó un intervalo de la forma \([b,\infty]\). En el último caso, \(b\) se llama mínima cota superior o supremo del conjunto \(C\) y se denota \(\sup C\). Por convención \(\sup\emptyset = -\infty\) y \(\sup C=\infty\) si \(C\) no es acotado por arriba.

Observación

Si \(C\) es finito, \(\sup C\) es el máximo de los elementos de \(C\) y típicamente se denota como \(\max C\).

Análogamente, \(a \in \mathbb{R}\) es una cota inferior en \(C \subseteq \mathbb{R}\) si

\[a \leq x, \forall x \in C.\]

El ínfimo o máxima cota inferior de \(C\) es \(\inf C = -\sup (-C)\). Por convención \(\inf \emptyset = \infty\) y si \(C\) no es acotado por debajo entonces \(\inf C = -\infty\).

Observación

Si \(C\) es finito, \(\inf C\) es el mínimo de sus elementos y se denota como \(\min C\).

---

Ejercicios

1. Resuelve los ejercicios y preguntas de la nota.

Preguntas de comprehensión

1)Menciona \(5\) propiedades que un conjunto debe cumplir para que sea considerado un espacio vectorial.

2)Menciona las propiedades que debe cumplir una función para que se considere una norma.

3)¿Qué es una norma matricial inducida? ¿qué mide una norma matricial inducida?

4)¿La norma de Frobenius es una norma matricial inducida?

5)¿A qué son iguales \(\text{sup}(\emptyset)\), \(\text{inf}(\emptyset)\) ? (el conjunto \(\emptyset\) es el conjunto vacío)

Referencias

1. L. Trefethen, D. Bau, Numerical linear algebra, SIAM, 1997.

2. G. H. Golub, C. F. Van Loan,Matrix Computations. John Hopkins University Press, 2013