1.5 Definición de función, continuidad y derivada
Contents
1.5 Definición de función, continuidad y derivada#
Notas para contenedor de docker:
Comando de docker para ejecución de la nota de forma local:
nota: cambiar <ruta a mi directorio> por la ruta de directorio que se desea mapear a /datos dentro del contenedor de docker y <versión imagen de docker> por la versión más actualizada que se presenta en la documentación.
docker run --rm -v <ruta a mi directorio>:/datos --name jupyterlab_optimizacion -p 8888:8888 -d palmoreck/jupyterlab_optimizacion:<versión imagen de docker>
password para jupyterlab: qwerty
Detener el contenedor de docker:
docker stop jupyterlab_optimizacion
Documentación de la imagen de docker palmoreck/jupyterlab_optimizacion:<versión imagen de docker> en liga.
Nota generada a partir de la liga1, liga2 e inicio de liga3.
Al final de esta nota la comunidad lectora:
Aprenderá las definiciones de función y derivada de una función en algunos casos de interés para el curso. En específico el caso de derivada direccional es muy importante.
Aprenderá que el gradiente y Hessiana de una función son un vector y una matriz de primeras (información de primer orden) y segundas derivadas (información de segundo orden) respectivamente.
Aprenderá algunas fórmulas utilizadas con el operador nabla de diferenciación.
Aprenderá la diferencia entre el cálculo algebraico o simbólico y el numérico vía el paquete SymPy.
Función#
Definición
Una función, \(f\), es una regla de correspondencia entre un conjunto nombrado dominio y otro conjunto nombrado codominio.
Notación#
\(f: A \rightarrow B\) es una función de un conjunto \(\text{dom}f \subseteq A\) en un conjunto \(B\).
Observación
\(\text{dom}f\) (el dominio de \(f\)) puede ser un subconjunto propio de \(A\), esto es, algunos elementos de \(A\) y otros no, son mapeados a elementos de \(B\).
En lo que sigue se considera al espacio \(\mathbb{R}^n\) y se asume que conjuntos y subconjuntos están en este espacio.
Conjunto abierto, cerrado, cerradura e interior#
Definición
El interior de un conjunto \(X\) es el conjunto de puntos interiores: un punto \(x\) de un conjunto \(X\) se llama interior si existe una vecindad de \(x\) (conjunto abierto* que contiene a \(x\)) contenida en \(X\).
*Un conjunto \(X\) se dice que es abierto si \(\forall x \in X\) existe una bola abierta* centrada en \(x\) y contenida en \(X\). Es equivalente escribir que \(X\) es abierto si su complemento \(\mathbb{R}^n \ X\) es cerrado.
*Una bola abierta con radio \(\epsilon>0\) y centrada en \(x\) es el conjunto: \(B_\epsilon(x) =\{y \in \mathbb{R}^n : ||y-x|| < \epsilon\}\). Ver Ejemplos de gráficas de normas en el plano para ejemplos de bolas abiertas en el plano.
En lo siguiente \(\text{intdom}f\) es el interior del dominio de \(f\).
Continuidad#
Definición
\(f: \mathbb{R}^n \rightarrow \mathbb{R}^m\) es continua en \(x \in \text{dom}f\) si \(\forall \epsilon >0 \exists \delta > 0\) tal que:
Comentarios
\(f\) continua en un punto \(x\) del dominio de \(f\) entonces \(f(y)\) es arbitrariamente cercana a \(f(x)\) para \(y\) en el dominio de \(f\) cercana a \(x\).
Otra forma de definir que \(f\) sea continua en \(x \in \text{dom}f\) es con sucesiones y límites: si \(\{x_i\}_{i \in \mathbb{N}} \subseteq \text{dom}f\) es una sucesión de puntos en el dominio de \(f\) que converge a \(x \in \text{dom}f\), \(\displaystyle \lim_{i \rightarrow \infty}x_i = x\), y \(f\) es continua en \(x\) entonces la sucesión \(\{f(x_i)\}_{i \in \mathbb{N}}\) converge a \(f(x)\): \(\displaystyle \lim_{i \rightarrow \infty}f(x_i) = f(x) = f \left(\displaystyle \lim_{i \rightarrow \infty} x_i \right )\).
Notación#
\(\mathcal{C}([a,b])=\{\text{funciones } f:\mathbb{R} \rightarrow \mathbb{R} \text{ continuas en el intervalo [a,b]}\}\) y \(\mathcal{C}(\text{dom}f) = \{\text{funciones } f:\mathbb{R}^n \rightarrow \mathbb{R}^m \text{ continuas en su dominio}\}\).
Función Diferenciable#
Caso \(f: \mathbb{R} \rightarrow \mathbb{R}\)#
Definición
\(f\) es diferenciable en \(x_0 \in (a,b)\) si \(\displaystyle \lim_{x \rightarrow x_0} \frac{f(x)-f(x_0)}{x-x_0}\) existe y escribimos:
\(f\) es diferenciable en \([a,b]\) si es diferenciable en cada punto de \([a,b]\). Análogamente definiendo la variable \(h=x-x_0\) se tiene:
\(f^{(1)}(x_0) = \displaystyle \lim_{h \rightarrow 0} \frac{f(x_0+h)-f(x_0)}{h}\) que típicamente se escribe como:
Comentario
Si \(f\) es diferenciable en \(x_0\) entonces \(f(x) \approx f(x_0) + f^{(1)}(x_0)(x-x_0)\). Gráficamente:
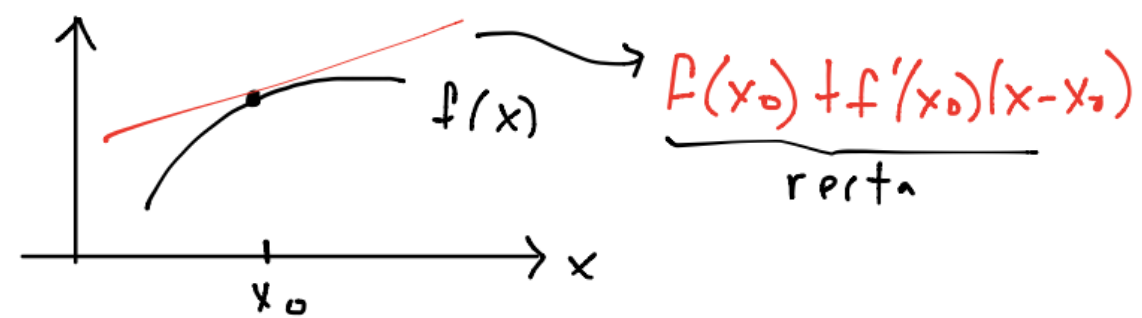
Como las derivadas también son funciones tenemos una notación para las derivadas que son continuas:
Notación#
\(\mathcal{C}^n([a,b])=\{\text{funciones } f:\mathbb{R} \rightarrow \mathbb{R} \text{ con } n \text{ derivadas continuas en el intervalo [a,b]}\}\).
En Python podemos utilizar el paquete SymPy para calcular límites y derivadas de forma simbólica (ver sympy/calculus) que es diferente al cálculo numérico que se revisa en Polinomios de Taylor y diferenciación numérica.
Ejemplo#
import sympy
Límite de \(\frac{\cos(x+h) - \cos(x)}{h}\) para \(h \rightarrow 0\):
x, h = sympy.symbols("x, h")
quotient = (sympy.cos(x+h) - sympy.cos(x))/h
sympy.pprint(sympy.limit(quotient, h, 0))
-sin(x)
Lo anterior corresponde a la derivada de \(\cos(x)\):
x = sympy.Symbol('x')
sympy.pprint(sympy.cos(x).diff(x))
-sin(x)
Si queremos evaluar la derivada podemos usar:
sympy.pprint(sympy.cos(x).diff(x).subs(x,sympy.pi/2))
-1
sympy.pprint(sympy.Derivative(sympy.cos(x), x))
d
──(cos(x))
dx
sympy.pprint(sympy.Derivative(sympy.cos(x), x).doit_numerically(sympy.pi/2))
-1.00000000000000
Caso \(f: \mathbb{R}^n \rightarrow \mathbb{R}^m\)#
Definición
\(f\) es diferenciable en \(x \in \text{intdom}f\) si existe una matriz \(Df(x) \in \mathbb{R}^{m\times n}\) tal que:
en este caso \(Df(x)\) se llama la derivada de \(f\) en \(x\).
Observación
Sólo puede existir a lo más una matriz que satisfaga el límite anterior.
Comentarios:
\(Df(x)\) también es llamada la Jacobiana de \(f\).
Se dice que \(f\) es diferenciable si \(\text{dom}f\) es abierto y es diferenciable en cada punto de \(\text{dom}f.\)
La función: \(f(x) + Df(x)(z-x)\) es afín y se le llama aproximación de orden \(1\) de \(f\) en \(x\) (o también cerca de \(x\)). Para \(z\) cercana a \(x\) ésta aproximación es cercana a \(f(z)\).
\(Df(x)\) puede encontrarse con la definición de límite anterior o con las derivadas parciales: \(Df(x)_{ij} = \frac{\partial f_i(x)}{\partial x_j}, i=1,\dots,m, j=1,\dots,n\) definidas como:
donde: \(f_i : \mathbb{R}^n \rightarrow \mathbb{R}\), \(i=1,\dots,m,j=1,\dots,n\) y \(e_j\) \(j\)-ésimo vector canónico que tiene un número \(1\) en la posición \(j\) y \(0\) en las entradas restantes.
Si \(f: \mathbb{R}^n \rightarrow \mathbb{R}, Df(x) \in \mathbb{R}^{1\times n}\), su transpuesta se llama gradiente, se denota \(\nabla f(x)\), es una función \(\nabla f : \mathbb{R}^n \rightarrow \mathbb{R}^n\), recibe un vector y devuelve un vector columna y sus componentes son derivadas parciales:
En este contexto, la aproximación de primer orden a \(f\) en \(x\) es: \(f(x) + \nabla f(x)^T(z-x)\) para \(z\) cercana a \(x\).
Notación#
\(\mathcal{C}^n(\text{dom}f) = \{\text{funciones } f:\mathbb{R}^n \rightarrow \mathbb{R}^m \text{ con } n \text{ derivadas continuas en su dominio}\}\).
Ejemplo#
\(f : \mathbb{R}^2 \rightarrow \mathbb{R}^2\) dada por:
con \(x = (x_1, x_2)^T\). Calcular la derivada de \(f\).
x1, x2 = sympy.symbols("x1, x2")
Definimos funciones \(f_1, f_2\) que son componentes del vector \(f(x)\).
f1 = x1*x2 + x2**2
sympy.pprint(f1)
2
x₁⋅x₂ + x₂
f2 = x1**2 + x2**2 + 2*x1*x2
sympy.pprint(f2)
2 2
x₁ + 2⋅x₁⋅x₂ + x₂
Derivadas parciales:
Para \(f_1(x) = x_1x_2 + x_2^2\):
df1_x1 = f1.diff(x1)
sympy.pprint(df1_x1)
x₂
df1_x2 = f1.diff(x2)
sympy.pprint(df1_x2)
x₁ + 2⋅x₂
Para \(f_2(x) = x_1^2 + 2x_1 x_2 + x_2^2\):
df2_x1 = f2.diff(x1)
sympy.pprint(df2_x1)
2⋅x₁ + 2⋅x₂
df2_x2 = f2.diff(x2)
sympy.pprint(df2_x2)
2⋅x₁ + 2⋅x₂
Entonces la derivada es:
Otra opción más fácil es utilizando Matrices:
f = sympy.Matrix([f1, f2])
sympy.pprint(f)
⎡ 2 ⎤
⎢ x₁⋅x₂ + x₂ ⎥
⎢ ⎥
⎢ 2 2⎥
⎣x₁ + 2⋅x₁⋅x₂ + x₂ ⎦
sympy.pprint(f.jacobian([x1, x2]))
⎡ x₂ x₁ + 2⋅x₂ ⎤
⎢ ⎥
⎣2⋅x₁ + 2⋅x₂ 2⋅x₁ + 2⋅x₂⎦
Para evaluar por ejemplo en \((x_1, x_2)^T = (0, 1)^T\):
d = f.jacobian([x1, x2])
sympy.pprint(d.subs([(x1, 0), (x2, 1)]))
⎡1 2⎤
⎢ ⎥
⎣2 2⎦
Regla de la cadena#
Definición
Si \(f:\mathbb{R}^n \rightarrow \mathbb{R}^m\) es diferenciable en \(x\in \text{intdom}f\) y \(g:\mathbb{R}^m \rightarrow \mathbb{R}^p\) es diferenciable en \(f(x)\in \text{intdom}g\), se define la composición \(h:\mathbb{R}^n \rightarrow \mathbb{R}^p\) por \(h(z) = g(f(z))\), la cual es diferenciable en \(x\), con derivada:
Ejemplo#
Sean \(f:\mathbb{R}^n \rightarrow \mathbb{R}\), \(g:\mathbb{R} \rightarrow \mathbb{R}\), \(h:\mathbb{R}^n \rightarrow \mathbb{R}\) con \(h(z) = g(f(z))\) entonces:
y la transpuesta de \(Dh(x)\) es: \(\nabla h(x) = Dh(x)^T = \frac{dg(f(x))}{dx} \nabla f(x) \in \mathbb{R}^{n\times 1}\).
Ejemplo#
\(f(x) = \cos(x), g(x)=\sin(x)\) por lo que \(h(x) = \sin(\cos(x))\). Calcular la derivada de \(h\).
x = sympy.Symbol('x')
f = sympy.cos(x)
sympy.pprint(f)
cos(x)
g = sympy.sin(x)
sympy.pprint(g)
sin(x)
h = g.subs(x, f)
sympy.pprint(h)
sin(cos(x))
sympy.pprint(h.diff(x))
-sin(x)⋅cos(cos(x))
Otras formas para calcular la derivada de la composición \(h\):
g = sympy.sin
h = g(f)
sympy.pprint(h.diff(x))
-sin(x)⋅cos(cos(x))
h = sympy.sin(f)
sympy.pprint(h.diff(x))
-sin(x)⋅cos(cos(x))
Ejemplo#
\(f(x) = x_1 + \frac{1}{x_2}, g(x) = e^x\) por lo que \(h(x) = e^{x_1 + \frac{1}{x_2}}\). Calcular la derivada de \(h\).
x1, x2 = sympy.symbols("x1, x2")
f = x1 + 1/x2
sympy.pprint(f)
1
x₁ + ──
x₂
g = sympy.exp
sympy.pprint(g)
exp
h = g(f)
sympy.pprint(h)
1
x₁ + ──
x₂
ℯ
sympy.pprint(h.diff(x1))
1
x₁ + ──
x₂
ℯ
sympy.pprint(h.diff(x2))
1
x₁ + ──
x₂
-ℯ
──────────
2
x₂
Otra forma para calcular el gradiente de \(h\) (derivada de \(h\)) es utilizando how-to-get-the-gradient-and-hessian-sympy:
from sympy.tensor.array import derive_by_array
sympy.pprint(derive_by_array(h, (x1, x2)))
⎡ 1 ⎤
⎢ 1 x₁ + ── ⎥
⎢ x₁ + ── x₂ ⎥
⎢ x₂ -ℯ ⎥
⎢ℯ ──────────⎥
⎢ 2 ⎥
⎣ x₂ ⎦
Caso particular#
Sean:
\(f: \mathbb{R}^n \rightarrow \mathbb{R}^m\), \(f(x) = Ax +b\) con \(A \in \mathbb{R}^{m\times n},b \in \mathbb{R}^m\),
\(g:\mathbb{R}^m \rightarrow \mathbb{R}^p\),
\(h: \mathbb{R}^n \rightarrow \mathbb{R}^p\), \(h(x)=g(f(x))=g(Ax+b)\) con \(\text{dom}h=\{z \in \mathbb{R}^n | Az+b \in \text{dom}g\}\) entonces:
Observación
Si \(p=1\), \(g: \mathbb{R}^m \rightarrow \mathbb{R}\), \(h: \mathbb{R}^n \rightarrow \mathbb{R}\) se tiene:
Ejemplo#
Este caso particular considera un caso importante en el que se tienen funciones restringidas a una línea. Si \(f: \mathbb{R}^n \rightarrow \mathbb{R}\), \(g: \mathbb{R} \rightarrow \mathbb{R}\) está dada por \(g(t) = f(x+tv)\) con \(x, v \in \mathbb{R}^n\) y \(t \in \mathbb{R}\), entonces escribimos que \(g\) es \(f\) pero restringida a la línea \(x+tv\). La derivada de \(g\) es:
El escalar \(Dg(0) = \nabla f(x)^Tv\) se llama derivada direccional de \(f\) en \(x\) en la dirección \(v\). Un dibujo en el que se considera \(\Delta x: = v\):
Como ejemplo considérese \(f(x) = x_1 ^2 + x_2^2\) con \(x=(x_1, x_2)^T\) y \(g(t) = f(x+tv)\) para \(v=(v_1, v_2)^T\) vector fijo y \(t \in \mathbb{R}\). Calcular \(Dg(t)\).
Primera opción
x1, x2 = sympy.symbols("x1, x2")
f = x1**2 + x2**2
sympy.pprint(f)
2 2
x₁ + x₂
t = sympy.Symbol('t')
v1, v2 = sympy.symbols("v1, v2")
new_args_for_f_function = {"x1": x1+t*v1, "x2": x2 + t*v2}
g = f.subs(new_args_for_f_function)
sympy.pprint(g)
2 2
(t⋅v₁ + x₁) + (t⋅v₂ + x₂)
sympy.pprint(g.diff(t))
2⋅v₁⋅(t⋅v₁ + x₁) + 2⋅v₂⋅(t⋅v₂ + x₂)
Segunda opción para calcular la derivada utilizando vectores:
x = sympy.Matrix([x1, x2])
sympy.pprint(x)
⎡x₁⎤
⎢ ⎥
⎣x₂⎦
v = sympy.Matrix([v1, v2])
new_arg_f_function = x+t*v
sympy.pprint(new_arg_f_function)
⎡t⋅v₁ + x₁⎤
⎢ ⎥
⎣t⋅v₂ + x₂⎦
mapping_for_g_function = {"x1": new_arg_f_function[0],
"x2": new_arg_f_function[1]}
g = f.subs(mapping_for_g_function)
sympy.pprint(g)
2 2
(t⋅v₁ + x₁) + (t⋅v₂ + x₂)
sympy.pprint(g.diff(t))
2⋅v₁⋅(t⋅v₁ + x₁) + 2⋅v₂⋅(t⋅v₂ + x₂)
Tercera opción definiendo a la función \(f\) a partir de \(x\) symbol Matrix:
sympy.pprint(x)
⎡x₁⎤
⎢ ⎥
⎣x₂⎦
f = x[0]**2 + x[1]**2
sympy.pprint(f)
2 2
x₁ + x₂
sympy.pprint(new_arg_f_function)
⎡t⋅v₁ + x₁⎤
⎢ ⎥
⎣t⋅v₂ + x₂⎦
g = f.subs({"x1": new_arg_f_function[0],
"x2": new_arg_f_function[1]})
sympy.pprint(g)
2 2
(t⋅v₁ + x₁) + (t⋅v₂ + x₂)
sympy.pprint(g.diff(t))
2⋅v₁⋅(t⋅v₁ + x₁) + 2⋅v₂⋅(t⋅v₂ + x₂)
En lo siguiente se utiliza derive-by_array, how-to-get-the-gradient-and-hessian-sympy para mostrar cómo se puede hacer un producto punto con SymPy
sympy.pprint(derive_by_array(f, x))
⎡2⋅x₁⎤
⎢ ⎥
⎣2⋅x₂⎦
sympy.pprint(derive_by_array(f, x).subs({"x1": new_arg_f_function[0],
"x2": new_arg_f_function[1]}))
⎡2⋅t⋅v₁ + 2⋅x₁⎤
⎢ ⎥
⎣2⋅t⋅v₂ + 2⋅x₂⎦
gradient_f_new_arg = derive_by_array(f, x).subs({"x1": new_arg_f_function[0],
"x2": new_arg_f_function[1]})
sympy.pprint(v)
⎡v₁⎤
⎢ ⎥
⎣v₂⎦
sympy.pprint(v.dot(gradient_f_new_arg))
v₁⋅(2⋅t⋅v₁ + 2⋅x₁) + v₂⋅(2⋅t⋅v₂ + 2⋅x₂)
Ejemplo#
Si \(h: \mathbb{R}^n \rightarrow \mathbb{R}\) dada por \(h(x) = \log \left( \displaystyle \sum_{i=1}^m \exp(a_i^Tx+b_i) \right)\) con \(x\in \mathbb{R}^n,a_i\in \mathbb{R}^n \forall i=1,\dots,m\) y \(b_i \in \mathbb{R} \forall i=1,\dots,m\) entonces:
donde: \(A=(a_i)_{i=1}^m \in \mathbb{R}^{m\times n}, b \in \mathbb{R}^m\), \(z=\left[ \begin{array}{c} \exp(a_1^Tx+b_1)\\ \vdots\\ \exp(a_m^Tx+b_m) \end{array}\right]\) y \(1 \in \mathbb{R}^m\) es un vector con entradas iguales a \(1\). Por lo tanto \(\nabla h(x) = (1^Tz)^{-1}A^Tz\).
En este ejemplo \(Dh(x) = Dg(f(x))Df(x)\) con:
\(h(x)=g(f(x))\),
\(g: \mathbb{R}^m \rightarrow \mathbb{R}\) dada por \(g(y)=\log \left( \displaystyle \sum_{i=1}^m \exp(y_i) \right )\),
\(f(x)=Ax+b.\)
Para lo siguiente se utilizó como referencias: liga1, liga2, liga3, liga4, liga5, liga6.
m = sympy.Symbol('m')
n = sympy.Symbol('n')
y = sympy.IndexedBase('y')
i = sympy.Symbol('i') #for index of sum
g = sympy.log(sympy.Sum(sympy.exp(y[i]), (i, 1, m)))
sympy.pprint(g)
⎛ m ⎞
⎜ ___ ⎟
⎜ ╲ ⎟
⎜ ╲ y[i]⎟
log⎜ ╱ ℯ ⎟
⎜ ╱ ⎟
⎜ ‾‾‾ ⎟
⎝i = 1 ⎠
Para un caso de \(m=3\) en la función \(g\) se tiene:
y1, y2, y3 = sympy.symbols("y1, y2, y3")
g_m_3 = sympy.log(sympy.exp(y1) + sympy.exp(y2) + sympy.exp(y3))
sympy.pprint(g_m_3)
⎛ y₁ y₂ y₃⎞
log⎝ℯ + ℯ + ℯ ⎠
dg_m_3 = derive_by_array(g_m_3, [y1, y2, y3])
sympy.pprint(dg_m_3)
⎡ y₁ y₂ y₃ ⎤
⎢ ℯ ℯ ℯ ⎥
⎢─────────────── ─────────────── ───────────────⎥
⎢ y₁ y₂ y₃ y₁ y₂ y₃ y₁ y₂ y₃⎥
⎣ℯ + ℯ + ℯ ℯ + ℯ + ℯ ℯ + ℯ + ℯ ⎦
sympy.pprint(derive_by_array(g, [y[1], y[2], y[3]]))
⎡ m m m ⎤
⎢ ____ ____ ____ ⎥
⎢ ╲ ╲ ╲ ⎥
⎢ ╲ ╲ ╲ ⎥
⎢ ╲ y[i] ╲ y[i] ╲ y[i] ⎥
⎢ ╱ ℯ ⋅δ ╱ ℯ ⋅δ ╱ ℯ ⋅δ ⎥
⎢ ╱ 1,i ╱ 2,i ╱ 3,i⎥
⎢ ╱ ╱ ╱ ⎥
⎢ ‾‾‾‾ ‾‾‾‾ ‾‾‾‾ ⎥
⎢i = 1 i = 1 i = 1 ⎥
⎢──────────────── ──────────────── ────────────────⎥
⎢ m m m ⎥
⎢ ___ ___ ___ ⎥
⎢ ╲ ╲ ╲ ⎥
⎢ ╲ y[i] ╲ y[i] ╲ y[i] ⎥
⎢ ╱ ℯ ╱ ℯ ╱ ℯ ⎥
⎢ ╱ ╱ ╱ ⎥
⎢ ‾‾‾ ‾‾‾ ‾‾‾ ⎥
⎣ i = 1 i = 1 i = 1 ⎦
Para la composición \(h(x) = g(f(x))\) se utilizan las siguientes celdas:
A = sympy.IndexedBase('A')
x = sympy.IndexedBase('x')
j = sympy.Symbol('j')
b = sympy.IndexedBase('b')
#we want something like:
sympy.pprint(sympy.exp(sympy.Sum(A[i, j]*x[j], (j, 1, n)) + b[i]))
n
___
╲
╲
b[i] + ╱ A[i, j]⋅x[j]
╱
‾‾‾
j = 1
ℯ
#better if we split each step:
arg_sum = A[i, j]*x[j]
sympy.pprint(arg_sum)
A[i, j]⋅x[j]
arg_exp = sympy.Sum(arg_sum, (j, 1, n)) + b[i]
sympy.pprint(arg_exp)
n
___
╲
╲
b[i] + ╱ A[i, j]⋅x[j]
╱
‾‾‾
j = 1
sympy.pprint(sympy.exp(arg_exp))
n
___
╲
╲
b[i] + ╱ A[i, j]⋅x[j]
╱
‾‾‾
j = 1
ℯ
arg_2_sum = sympy.exp(arg_exp)
sympy.pprint(sympy.Sum(arg_2_sum, (i, 1, m)))
m
_______
╲
╲
╲ n
╲ ___
╲ ╲
╲ ╲
╱ b[i] + ╱ A[i, j]⋅x[j]
╱ ╱
╱ ‾‾‾
╱ j = 1
╱ ℯ
╱
‾‾‾‾‾‾‾
i = 1
h = sympy.log(sympy.Sum(arg_2_sum, (i, 1, m)))
#complex expression: sympy.log(sympy.Sum(sympy.exp(sympy.Sum(A[i, j]*x[j], (j, 1, n)) + b[i]), (i, 1, m)))
sympy.pprint(h)
⎛ m ⎞
⎜_______ ⎟
⎜╲ ⎟
⎜ ╲ ⎟
⎜ ╲ n ⎟
⎜ ╲ ___ ⎟
⎜ ╲ ╲ ⎟
⎜ ╲ ╲ ⎟
log⎜ ╱ b[i] + ╱ A[i, j]⋅x[j]⎟
⎜ ╱ ╱ ⎟
⎜ ╱ ‾‾‾ ⎟
⎜ ╱ j = 1 ⎟
⎜ ╱ ℯ ⎟
⎜╱ ⎟
⎜‾‾‾‾‾‾‾ ⎟
⎝ i = 1 ⎠
sympy.pprint(h.diff(x[1]))
m
________
╲
╲ n
╲ ___
╲ ╲
╲ ╲
╲ b[i] + ╱ A[i, j]⋅x[j] n
╲ ╱ ___
╱ ‾‾‾ ╲
╱ j = 1 ╲ δ ⋅A[i, j]
╱ ℯ ⋅ ╱ 1,j
╱ ╱
╱ ‾‾‾
╱ j = 1
╱
‾‾‾‾‾‾‾‾
i = 1
──────────────────────────────────────────────────────
m
_______
╲
╲
╲ n
╲ ___
╲ ╲
╲ ╲
╱ b[i] + ╱ A[i, j]⋅x[j]
╱ ╱
╱ ‾‾‾
╱ j = 1
╱ ℯ
╱
‾‾‾‾‾‾‾
i = 1
sympy.pprint(derive_by_array(h, [x[1]])) #we can use also: derive_by_array(h, [x[1], x[2], x[3]]
⎡ m ⎤
⎢________ ⎥
⎢╲ ⎥
⎢ ╲ n ⎥
⎢ ╲ ___ ⎥
⎢ ╲ ╲ ⎥
⎢ ╲ ╲ ⎥
⎢ ╲ b[i] + ╱ A[i, j]⋅x[j] n ⎥
⎢ ╲ ╱ ___ ⎥
⎢ ╱ ‾‾‾ ╲ ⎥
⎢ ╱ j = 1 ╲ δ ⋅A[i, j]⎥
⎢ ╱ ℯ ⋅ ╱ 1,j ⎥
⎢ ╱ ╱ ⎥
⎢ ╱ ‾‾‾ ⎥
⎢ ╱ j = 1 ⎥
⎢╱ ⎥
⎢‾‾‾‾‾‾‾‾ ⎥
⎢ i = 1 ⎥
⎢──────────────────────────────────────────────────────⎥
⎢ m ⎥
⎢ _______ ⎥
⎢ ╲ ⎥
⎢ ╲ ⎥
⎢ ╲ n ⎥
⎢ ╲ ___ ⎥
⎢ ╲ ╲ ⎥
⎢ ╲ ╲ ⎥
⎢ ╱ b[i] + ╱ A[i, j]⋅x[j] ⎥
⎢ ╱ ╱ ⎥
⎢ ╱ ‾‾‾ ⎥
⎢ ╱ j = 1 ⎥
⎢ ╱ ℯ ⎥
⎢ ╱ ⎥
⎢ ‾‾‾‾‾‾‾ ⎥
⎣ i = 1 ⎦
Pregunta
Utilizando lenguajes de programación ¿se puede resolver este ejercicio con Matrix Symbol?
Ejercicio
Utilizando lenguajes de programación verificar que lo obtenido con SymPy es igual a lo desarrollado en “papel” al inicio del Ejemplo
Segunda derivada de una función \(f: \mathbb{R}^n \rightarrow \mathbb{R}\).#
Definición
Sea \(f:\mathbb{R}^n \rightarrow \mathbb{R}\). La segunda derivada o matriz Hessiana de \(f\) en \(x \in \text{intdom}f\) existe si \(f\) es dos veces diferenciable en \(x\), se denota \(\nabla^2f(x)\) y sus componentes son segundas derivadas parciales:
Comentarios:
La aproximación de segundo orden a \(f\) en \(x\) (o también para puntos cercanos a \(x\)) es la función cuadrática en la variable \(z\):
Se cumple:
Se tiene lo siguiente:
\(\nabla f\) es una función nombrada gradient mapping (o simplemente gradiente).
\(\nabla f:\mathbb{R}^n \rightarrow \mathbb{R}^n\) tiene regla de correspondencia \(\nabla f(x)\) (evaluar en \(x\) la matriz \(Df(\cdot)^T\)).
Se dice que \(f\) es dos veces diferenciable en \(\text{dom}f\) si \(\text{dom}f\) es abierto y \(f\) es dos veces diferenciable en cada punto de \(x\).
\(D\nabla f(x) = \nabla^2f(x)\) para \(x \in \text{intdom}f\).
\(\nabla ^2 f(x) : \mathbb{R}^n \rightarrow \mathbb{R}^{n \times n}\).
Si \(f \in \mathcal{C}^2(\text{dom}f)\) entonces la Hessiana es una matriz simétrica.
Regla de la cadena para la segunda derivada#
Caso particular#
Sean:
\(f:\mathbb{R}^n \rightarrow \mathbb{R}\),
\(g:\mathbb{R} \rightarrow \mathbb{R}\),
\(h:\mathbb{R}^n \rightarrow \mathbb{R}\) con \(h(x) = g(f(x))\), entonces:
y
por lo que:
Caso particular#
Sean:
\(f:\mathbb{R}^n \rightarrow \mathbb{R}^m, f(x) = Ax+b\) con \(A \in \mathbb{R}^{m\times n}\), \(b \in \mathbb{R}^m\),
\(g:\mathbb{R}^m \rightarrow \mathbb{R}^p\),
\(h:\mathbb{R}^n \rightarrow \mathbb{R}^p\), \(h(x) = g(f(x)) = g(Ax+b)\) con \(\text{dom}h=\{z \in \mathbb{R}^n | Az+b \in \text{dom}g\}\) entonces:
Observación
Si \(p=1\), \(g: \mathbb{R}^m \rightarrow \mathbb{R}\), \(h: \mathbb{R}^n \rightarrow \mathbb{R}\) se tiene:
Ejemplo#
Si \(f:\mathbb{R}^n \rightarrow \mathbb{R}\), \(g: \mathbb{R} \rightarrow \mathbb{R}\) está dada por \(g(t) = f(x+tv)\) con \(x,v \in \mathbb{R}^n, t \in \mathbb{R}\), esto es, \(g\) es \(f\) pero restringida a la línea \(\{x+tv|t \in \mathbb{R}\}\) , entonces:
Por lo que:
Ejemplo#
Si \(h: \mathbb{R}^n \rightarrow \mathbb{R}, h(x) = \log \left( \displaystyle \sum_{i=1}^m \exp(a_i^Tx+b_i)\right)\) con \(x \in \mathbb{R}^n, a_i \in \mathbb{R}^n \forall i=1,\dots,m\) y \(b_i \in \mathbb{R} \forall i=1,\dots,m\).
Como se desarrolló anteriormente \(\nabla h(x) = (1^Tz)^{-1}A^Tz\) con \(z=\left[ \begin{array}{c} \exp(a_1^Tx+b_1)\\ \vdots\\ \exp(a_m^Tx+b_m) \end{array}\right]\) y \(A=(a_i)_{i=1}^m \in \mathbb{R}^{m\times n}.\)
Por lo que
donde: \(\nabla^2g(y)=(1^Ty)^{-1}\text{diag}(y)-(1^Ty)^{-2}yy^T\).
y \(\text{diag}(c)\) es una matriz diagonal con elementos en su diagonal iguales a las entradas del vector \(c\).
Ejercicio
Utilizando lenguajes de programación verificar con el paquete de SymPy las expresiones para la segunda derivada de los dos ejemplos anteriores.
Tablita útil para fórmulas de diferenciación con el operador \(\nabla\)#
Sean \(f,g:\mathbb{R}^n \rightarrow \mathbb{R}\) con \(f,g \in \mathcal{C}^2\) respectivamente en sus dominios y \(\alpha_1, \alpha_2 \in \mathbb{R}\), \(A \in \mathbb{R}^{n \times n}\), \(b \in \mathbb{R}^n\) son fijas. Diferenciando con respecto a la variable \(x \in \mathbb{R}^n\) se tiene:
linealidad |
\(\nabla(\alpha_1 f(x) + \alpha_2 g(x)) = \alpha_1 \nabla f(x) + \alpha_2 \nabla g(x)\) |
producto |
\(\nabla(f(x)g(x)) = \nabla f(x) g(x) + f(x) \nabla g(x)\) |
producto punto |
\(\nabla(b^Tx) = b\) |
cuadrático |
\(\nabla(x^TAx) = 2(A+A^T)x\) |
segunda derivada |
\(\nabla^2(Ax)=A\) |
Comentario respecto al cómputo simbólico o algebraico y númerico#
Si bien el cómputo simbólico o algebraico nos ayuda a calcular las expresiones para las derivadas evitando los problemas de errores por redondeo que se revisarán en Polinomios de Taylor y diferenciación numérica, la complejidad de las expresiones que internamente se manejan es ineficiente vs el cómputo numérico, ver Computer science aspects of computer algebra y GNU_Multiple_Precision_Arithmetic_Library.
Como ejemplo de la precisión arbitraria que se puede manejar con el cómputo simbólico o algebraico vs el Sistema en punto flotante considérese el cálculo siguiente:
eps = 1-3*(4/3-1)
print("{:0.16e}".format(eps))
'2.2204460492503131e-16'
eps_sympy = 1-3*(sympy.Rational(4,3)-1)
print("{:0.16e}".format(float(eps_sympy)))
'0.0000000000000000e+00'
Ejercicios
1.Resuelve los ejercicios y preguntas de la nota.
Referencias
S. P. Boyd, L. Vandenberghe, Convex Optimization. Cambridge University Press, 2004.

