3.1 Definición de problemas de optimización, conjuntos y funciones convexas
Contents
3.1 Definición de problemas de optimización, conjuntos y funciones convexas#
Notas para contenedor de docker:
Comando de docker para ejecución de la nota de forma local:
nota: cambiar <ruta a mi directorio> por la ruta de directorio que se desea mapear a /datos dentro del contenedor de docker y <versión imagen de docker> por la versión más actualizada que se presenta en la documentación.
docker run --rm -v <ruta a mi directorio>:/datos --name jupyterlab_optimizacion -p 8888:8888 -d palmoreck/jupyterlab_optimizacion:<versión imagen de docker>
password para jupyterlab: qwerty
Detener el contenedor de docker:
docker stop jupyterlab_optimizacion
Documentación de la imagen de docker palmoreck/jupyterlab_optimizacion:<versión imagen de docker> en liga.
Nota generada a partir de liga1, liga2, liga3, liga4, liga5, liga6.
Al final de esta nota la comunidad lectora:
Conocerá la definición de un problema de optimización, algunos ejemplos, definiciones y resultados que serán utilizados en los métodos para resolver problemas de optimización con énfasis en funciones convexas.
Tendrá una lista ejemplo de funciones convexas utilizadas en aplicaciones.
¿Problemas de optimización numérica?#
Una gran cantidad de aplicaciones plantean problemas de optimización. Tenemos problemas básicos que se presentan en cursos iniciales de cálculo:
Una caja con base y tapa cuadradas debe tener un volumen de \(100 cm^3\). Encuentre las dimensiones de la caja que minimicen la cantidad de material.
Y tenemos más especializados que encontramos en áreas como Estadística, Ingeniería, Finanzas o Aprendizaje de Máquina, Machine Learning:
Ajustar un modelo de regresión lineal a un conjunto de datos.
Buscar la mejor forma de invertir un capital en un conjunto de activos.
Elección del ancho y largo de un dispositivo en un circuito electrónico.
Ajustar un modelo que clasifique un conjunto de datos.
En general un problema de optimización matemática o numérica tiene la forma:
donde: \(x=(x_1,x_2,\dots, x_n)^T\) es la variable de optimización del problema, la función \(f_o: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es la función objetivo, las funciones \(f_i: \mathbb{R}^n \rightarrow \mathbb{R}, i=1,\dots,m\) son las funciones de restricción (aquí se colocan únicamente desigualdades pero pueden ser sólo igualdades o bien una combinación de ellas) y las constantes \(b_1,b_2,\dots, b_m\) son los límites o cotas de las restricciones.
Un vector \(x^* \in \mathbb{R}^n\) es nombrado óptimo o solución del problema anterior si tiene el valor más pequeño de entre todos los vectores \(x \in \mathbb{R}^n\) que satisfacen las restricciones. Por ejemplo, si \(z \in \mathbb{R}^n\) satisface \(f_1(z) \leq b_1, f_2(z) \leq b_2, \dots, f_m(z) \leq b_m\) y \(x^*\) es óptimo entonces \(f_o(z) \geq f_o(x^*)\).
Comentarios
Se consideran funciones objetivo \(f_o: \mathbb{R}^n \rightarrow \mathbb{R}\), sin embargo, hay formulaciones que utilizan \(f_o: \mathbb{R}^n \rightarrow \mathbb{R}^q\). Tales formulaciones pueden hallarlas en la optimización multicriterio, multiobjetivo, vectorial o también nombrada Pareto, ver Multi objective optimization.
El problema de optimización definido utiliza una forma de minimización y no de maximización. Típicamente en la literatura por convención se consideran problemas de este tipo. Además minimizar \(f_o\) y maximizar \(-f_o\) son problemas de optimización equivalentes.
Ejemplo#
con \(A \in \mathbb{R}^{m \times n}, b \in \mathbb{R}^m\). En este problema buscamos el vector \(x\) que es solución del problema \(Ax \leq b\) con mínima norma Euclidiana. La función objetivo es \(f_o(x)=||x||_2\), las funciones de restricción son las desigualdades lineales \(f_i(x) = a_i^Tx \leq b_i\) con \(a_i\) \(i\)-ésimo renglón de \(A\) y \(b_i\) \(i\)-ésima componente de \(b\), \(\forall i=1,\dots,m\).
Comentario
Un problema similar (sólo modificando desigualdad por igualdad) lo encontramos al resolver un sistema de ecuaciones lineales \(Ax=b\) underdetermined en el que \(m < n\) y se busca el vector \(x\) con mínima norma Euclidiana que satisfaga tal sistema. Este sistema puede tener infinitas soluciones o ninguna solución.
Ejemplo#
Encuentra el punto en la gráfica de \(y=x^2\) que es más cercano al punto \(P=(1,0)\) bajo la norma Euclidiana.
Deseamos minimizar la cantidad \(||(1,0)-(x,y)||_2\). Además \(y = y(x)\) por lo que definiendo la función objetivo \(f_o(x) = ||(1,0)-(x,x^2)||_2=||(1-x,-x^2)||_2=\sqrt{(1-x)^2+x^4}\), el problema de optimización (sin restricciones) es:
Optimización numérica en ciencia de datos#
La ciencia de datos apunta al desarrollo de técnicas y se apoya de aplicaciones de machine learning para la extracción de conocimiento útil tomando como fuente de información las grandes cantidades de datos. Algunas de las aplicaciones son:
Clasificación de documentos o textos: detección de spam.
Procesamiento de lenguaje natural: named-entity recognition.
Visión por computadora: reconocimiento de rostros o imágenes.
Detección de fraude.
Diagnóstico médico.
Las aplicaciones anteriores involucran problemas como son:
Clasificación.
Regresión.
Ranking.
Clustering.
Reducción de la dimensionalidad.
Optimización numérica y machine learning#
En cada una de las aplicaciones o problemas anteriores se utilizan funciones de pérdida que guían el proceso de aprendizaje. Tal proceso involucra optimización parámetros de la función de pérdida. Por ejemplo, si la función de pérdida en un problema de regresión es una pérdida cuadrática \(\mathcal{L}(y,\hat{y}) = (\hat{y}-y)^2\) con \(\hat{y} = \hat{\beta}_0 + \hat{\beta_1}x\), entonces el vector de parámetros a optimizar (aprender) es \(\beta= \left[ \begin{array}{c} \beta_0\\ \beta_1 \end{array} \right]\).
Machine learning no sólo se apoya de la optimización pues es un área de Inteligencia Artificial que utiliza técnicas estadísticas para el diseño de sistemas capaces de aplicaciones como las escritas anteriormente, de modo que hoy en día tenemos statistical machine learning. No obstante, uno de los pilares de machine learning o statistical machine learning es la optimización.
Machine learning o statistical machine learning se apoya de las formulaciones y algoritmos en optimización. Sin embargo, también ha contribuido a ésta área desarrollando nuevos enfoques en los métodos o algoritmos para el tratamiento de grandes cantidades de datos o big data y estableciendo retos significativos no presentes en problemas clásicos de optimización. De hecho, al revisar literatura que intersecta estas dos disciplinas encontramos comunidades científicas que desarrollan o utilizan métodos o algoritmos exactos (ver Exact algorithm) y otras que utilizan métodos de optimización estocástica (ver Stochastic optimization y Stochastic approximation) basados en métodos o algoritmos aproximados (ver Approximation algorithm). Hoy en día es común encontrar estudios que hacen referencia a modelos o métodos de aprendizaje.
Observación
Como ejemplo de lo anterior considérese la técnica de regularización que en machine learning se utiliza para encontrar soluciones que generalicen y provean una explicación no compleja del fenómeno en estudio.
La regularización sigue el principio de la navaja de Occam, ver Occam’s razor: para cualquier conjunto de observaciones en general se prefieren explicaciones simples a explicaciones más complicadas. Aunque la técnica de regularización es conocida en optimización, han sido varias las aplicaciones de machine learning las que la han posicionado como clave.
Del small scale al large scale machine learning#
El inicio del siglo XXI estuvo marcado, entre otros temas, por un incremento significativo en la generación de información. Esto puede contrastarse con el desarrollo de los procesadores de las máquinas, el cual tuvo un menor avance en el incremento del performance al del siglo XX. Asimismo, las mejoras en dispositivos de almacenamiento o storage abarató costos de almacenamiento y mejoras en sistemas de networking permitieron la transmisión de la información más eficiente. En este contexto, los modelos y métodos de statistical machine learning se vieron limitados por el tiempo de cómputo y no por el tamaño de muestra. La conclusión de esto fue una inclinación en la comunidad científica por el diseño o uso de métodos o modelos para procesar grandes cantidades de datos usando recursos computacionales comparativamente menores.
¿Optimización numérica convexa?#
Aplicaciones de machine learning conducen al planteamiento de problemas de optimización convexa y no convexa. Por ejemplo en la aplicación de clasificación de textos, en donde se desea asignar un texto a clases definidas de acuerdo a su contenido (determinar si un documento de texto es sobre un tema), puede formularse un problema convexo a partir de una función de pérdida convexa.
Como ejemplos de aplicaciones en la optimización no convexa están el reconocimiento de voz y reconocimiento de imágenes. El uso de redes neuronales profundas ha tenido muy buen desempeño en tales aplicaciones haciendo uso de cómputo en la GPU, ver ImageNet Classification with Deep Convolutional Neural Networks, 2012: A Breakthrough Year for Deep Learning. En este caso se utilizan funciones objetivo no lineales y no convexas.
Comentarios
Desde los \(40\)’s se han desarrollado algoritmos para resolver problemas de optimización, se han analizado sus propiedades y se han desarrollado buenas implementaciones de software. Sin embargo, una clase de problemas de optimización en los que encontramos métodos efectivos son los convexos.
Métodos para optimización no convexa utilizan parte de la teoría de convexidad desarrollada en optimización convexa. Además, un buen número de problemas de aprendizaje utilizan funciones de pérdida convexas.
Problema estándar de optimización#
En lo que continúa se considera \(f_0 = f_o\) (el subíndice “0” y el subíndice “o” son iguales)
Definición
Un problema estándar de optimización es:
con \(x=(x_1,x_2,\dots, x_n)^T\) es la variable de optimización del problema, \(f_o: \mathbb{R}^n \rightarrow \mathbb{R}\) es la función objetivo, \(f_i: \mathbb{R}^n \rightarrow \mathbb{R}\) \(\forall i=1,\dots,m\) son las restricciones de desigualdad, \(h_i: \mathbb{R}^n \rightarrow \mathbb{R}\), \(\forall i=1,\dots,p\) son las restricciones de igualdad.
Dominio del problema de optimización y puntos factibles#
Definiciones
El conjunto de puntos para los que la función objetivo y las funciones de restricción \(f_i, h_i\) están definidas se nombra dominio del problema de optimización, esto es:
Un punto \(x \in \mathcal{D}\) se nombra factible si satisface las restricciones de igualdad y desigualdad. El conjunto de puntos factibles se nombra conjunto de factibilidad.
El problema estándar de optimización se nombra problema de optimización factible si existe al menos un punto factible, si no entonces es infactible.
Valor óptimo del problema de optimización#
Definición
El valor óptimo del problema se denota como \(p^*\). En notación matemática es:
Comentarios
Si el problema es infactible entonces \(p^* = \infty\).
Si \(\exists x_k\) factible tal que \(f_o(x_k) \rightarrow -\infty\) para \(k \rightarrow \infty\) entonces \(p^*=-\infty\) y se nombra problema de optimización no acotado por debajo.
Punto óptimo del problema de optimización#
Definición
\(x^*\) es punto óptimo si es factible y \(f_o(x^*) = p^*\).
El conjunto de óptimos se nombra conjunto óptimo y se denota:
Comentarios
La propiedad de un punto óptimo \(x^*\) es que si \(z\) satisface las restricciones \(f_i(z) \leq 0\) \(\forall i=1,...,m\), \(h_i(z)=0\) \(\forall i=1,..,p\) se tiene: \(f_o(x^*) \leq f_o(z)\). Es óptimo estricto si \(z\) satisface las restricciones y \(f_o(x^*) < f_o(z)\).
Si existe un punto óptimo se dice que el valor óptimo se alcanza y por tanto el problema de optimización tiene solución, es soluble o solvable.
Si \(X_{\text{opt}} = \emptyset\) se dice que el valor óptimo no se alcanza. Obsérvese que para problemas no acotados nunca se alcanza el valor óptimo.
Si \(x\) es factible y \(f_o(x) \leq p^* + \epsilon\) con \(\epsilon >0\), \(x\) se nombra \(\epsilon\)-subóptimo y el conjunto de puntos \(\epsilon\)-subóptimos se nombra conjunto \(\epsilon\)-subóptimo.
Óptimo local#
Definición
Un punto factible \(x\) se nombra óptimo local si \(\exists R > 0\) tal que:
Así, \(x\) resuelve:
Observación
La palabra óptimo se utiliza para óptimo global, esto es, no consideramos la última restricción \(||z-x||_2 \leq R\) en el problema de optimización y exploramos en todo el \(\text{dom}f\).

Observación
Es común referirse al conjunto de mínimos y máximos como puntos extremos de una función.
Restricciones activas, no activas y redundantes#
Definición
Si \(x\) es factible y \(f_i(x)=0\) entonces la restricción de desigualdad \(f_i(x) \leq 0\) se nombra restricción activa en \(x\). Se nombra inactiva en \(x\) si \(f_i(x) <0\) para alguna \(i=1,\dots ,m\).
Comentarios
Las restricciones de igualdad, \(h_i(x)\), siempre son activas en el conjunto factible con \(i=1,\dots ,p\).
Una restricción se nombra restricción redundante si al quitarla el conjunto factible no se modifica.
Problemas de optimización convexa en su forma estándar o canónica#
Definición
Se define un problema de optimización convexa en su forma estándar o canónica como:
donde: \(f_i\) son convexas \(\forall i=0,1,\dots,m\) y \(h_i\) es afín \(\forall i =1,\dots,p\).
Comentarios
El conjunto de factibilidad de un problema de optimización convexa es un conjunto convexo. Esto se sigue pues es una intersección finita de conjuntos convexos: intersección entre las \(x\)’s que satisfacen \(f_i(x) \leq 0\), \(i=1,\dots ,m\), que se nombra conjunto subnivel, y las \(x\)’s que están en un hiperplano, esto es, que satisfacen \(h_i(x) = 0\), \(i=1,\dots ,p\).
Si en el problema anterior se tiene que maximizar una \(f_o\) función objetivo cóncava y se tienen misma forma estándar: \(f_i\) convexa, \(h_i\) afín entonces también se nombra al problema como problema de optimización convexa. Todos los resultados, conclusiones y algoritmos desarrollados para los problemas de minimización son aplicables para maximización. En este caso se puede resolver un problema de maximización al minimizar la función objetivo \(-f_o\) que es convexa.
Función convexa#
Definición
Sea \(f:\mathbb{R}^n \rightarrow \mathbb{R}\) una función con el conjunto \(\text{dom}f\) convexo. \(f\) se nombra convexa (en su \(\text{dom}f\)) si \(\forall x,y \in \text{dom}f\) y \(\theta \in [0,1]\) se cumple:
Si la desigualdad se cumple de forma estricta \(\forall x \neq y\) \(f\) se nombra estrictamente convexa.
Observaciones
La convexidad de \(f\) se define para \(\text{dom}f\) aunque para casos en particular se detalla el conjunto en el que \(f\) es convexa.
La desigualdad que define a funciones convexas se nombra desigualdad de Jensen.
Propiedades#
Entre las propiedades que tiene una función convexa se encuentran las siguientes:
Si \(f\) es convexa el conjunto subnivel es un conjunto convexo.
\(\text{dom}f\) es convexo \(\therefore\) \(\theta x + (1-\theta)y \in \text{dom}f\)
\(f\) es cóncava si \(-f\) es convexa y estrictamente cóncava si \(-f\) es estrictamente convexa. Otra forma de definir concavidad es con una desigualdad del tipo:
y mismas definiciones para \(x,y, \theta\) que en la definición de convexidad.
Si \(f\) es convexa, geométricamente el segmento de línea que se forma con los puntos \((x,f(x)), (y,f(y))\) está por encima o es igual a \(f(\theta x + (1-\theta)y) \forall \theta \in [0,1]\) y \(\forall x,y \in \text{dom}f\):
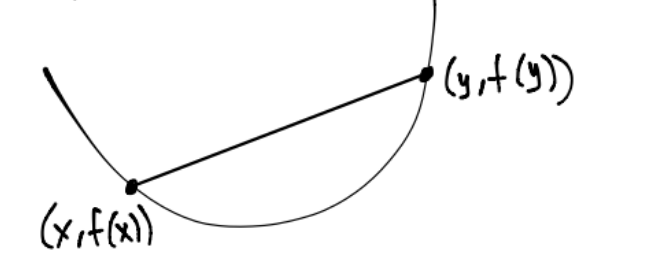
Conjuntos convexos#
Línea y segmentos de línea#
Definición
Sean \(x_1, x_2 \in \mathbb{R}^n\) con \(x_1 \neq x_2\). Entonces el punto:
con \(\theta \in \mathbb{R}\) se encuentra en la línea que pasa por \(x_1\) y \(x_2\). \(\theta\) se le nombra parámetro y si \(\theta \in [0,1]\) tenemos un segmento de línea:

Comentarios
\(y = \theta x_1 + (1-\theta)x_2 = x_2 + \theta(x_1 -x_2)\) y esta última igualdad se interpreta como “\(y\) es la suma del punto base \(x_2\) y la dirección \(x_1-x_2\) escalada por \(\theta\)”.
Si \(\theta=0\) entonces \(y=x_2\). Si \(\theta \in [0,1]\) entonces \(y\) se “mueve” en la dirección \(x_1-x_2\) hacia \(x_1\) y si \(\theta>1\) entonces \(y\) se encuentra en la línea “más allá” de \(x_1\):

El punto entre \(x_1\) y \(x_2\) tiene \(\theta=\frac{1}{2}\).
Conjunto convexo#
Definición
Un conjunto \(\mathcal{C}\) es convexo si el segmento de línea entre cualquier par de puntos de \(\mathcal{C}\) está completamente contenida en \(\mathcal{C}\). Esto se escribe matemáticamente como:
Ejemplos gráficos de conjuntos convexos:
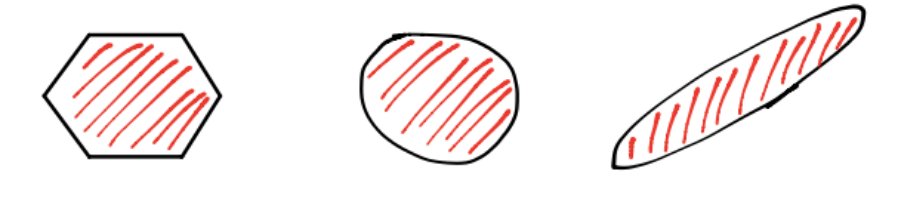
Ejemplos gráficos de conjuntos no convexos:

Comentarios
El punto \(\displaystyle \sum_{i=1}^k \theta_i x_i\) con \(\displaystyle \sum_{i=1}^k \theta_i=1\), \(\theta_i \geq 0 \forall i=1,\dots,k\) se nombra combinación convexa de los puntos \(x_1, x_2, \dots, x_k\). Una combinación convexa de los puntos \(x_1, \dots, x_k\) puede pensarse como una mezcla o promedio ponderado de los puntos, con \(\theta_i\) la fracción \(\theta_i\) de \(x_i\) en la mezcla.
Un conjunto es convexo si y sólo si contiene cualquier combinación convexa de sus puntos.
El conjunto óptimo y los conjuntos \(\epsilon\)-subóptimos son convexos. Ver definiciones de conjunto óptimo y \(\epsilon\)-subóptimos en punto óptimo del problema de optimización.
Ejemplos de funciones convexas y cóncavas#
Una función afín es convexa y cóncava en todo su dominio: \(f(x) = Ax+b\) con \(A \in \mathbb{R}^{m \times n}, b \in \mathbb{R}^m\), \(\text{dom}f = \mathbb{R}^n\).
Observación
Por tanto las funciones lineales también son convexas y cóncavas.
Funciones cuadráticas: \(f: \mathbb{R}^n \rightarrow \mathbb{R}\), \(f(x) = \frac{1}{2} x^TPx + q^Tx + r\) son convexas en su dominio \(\mathbb{R}^n\) si \(P \in \mathbb{S}_+^n, q \in \mathbb{R}^n, r \in \mathbb{R}\) con \(\mathbb{S}_+^n\) conjunto de matrices simétricas positivas semidefinidas.
Observación
Observa que por este punto la norma \(2\) o Euclidiana es una función convexa en \(\mathbb{R}^n\).
Definición
\(x^TPx\) con \(P \in \mathbb{S}^{n}_+\) se nombra forma cuadrática semidefinida positiva.
Comentario
La función \(f(x) = \frac{1}{2} x^TPx + q^Tx + r\) es estrictamente convexa si y sólo si \(P \in \mathbb{S}_{++}^n\). \(f\) es cóncava si y sólo si \(P \in -\mathbb{S}_+^n\).
Exponenciales: \(f: \mathbb{R} \rightarrow \mathbb{R}\), \(f(x) = e^{ax}\) para cualquier \(a \in \mathbb{R}\) es convexa en su dominio \(\mathbb{R}\).
Potencias: \(f: \mathbb{R} \rightarrow \mathbb{R}\), \(f(x)=x^a\):
Si \(a \geq 1\) o \(a \leq 0\) entonces \(f\) es convexa en \(\mathbb{R}_{++}\) (números reales positivos).
Si \(0 \leq a \leq 1\) entonces \(f\) es cóncava en \(\mathbb{R}_{++}\).
Potencias del valor absoluto: \(f: \mathbb{R} \rightarrow \mathbb{R}\), \(f(x)=|x|^p\) con \(p \geq 1\) es convexa en \(\mathbb{R}\).
Logaritmo: \(f: \mathbb{R} \rightarrow \mathbb{R}\), \(f(x) = \log(x)\) es cóncava en su dominio: \(\mathbb{R}_{++}\).
Entropía negativa: \(f(x) = \begin{cases} x\log(x) &\text{ si } x > 0 ,\\ 0 &\text{ si } x = 0 \end{cases}\) es estrictamente convexa en su dominio \(\mathbb{R}_+\).
Normas: cualquier norma es convexa en su dominio.
Función máximo: \(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\), \(f(x) = \max\{x_1,\dots,x_n\}\) es convexa.
Función log-sum-exp: \(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\), \(f(x)=\log\left(\displaystyle \sum_{i=1}^ne^{x_i}\right)\) es convexa en su dominio \(\mathbb{R}^n\).
La media geométrica: \(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\), \(f(x) = \left(\displaystyle \prod_{i=1}^n x_i \right)^\frac{1}{n}\) es cóncava en su dominio \(\mathbb{R}_{++}^n\).
Función log-determinante: \(f: \mathbb{S}^{n} \rightarrow \mathbb{R}^n\), \(f(x) = \log(\det(X))\) es cóncava en su dominio \(\mathbb{S}_{++}^n\).
Resultados útiles#
Sobre funciones convexas/cóncavas#
Sea \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) diferenciable entonces \(f\) es convexa si y sólo si \(\text{dom}f\) es un conjunto convexo y se cumple:
Si se cumple de forma estricta la desigualdad \(f\) se nombra estrictamente convexa. También si su \(\text{dom}f\) es convexo y se tiene la desigualdad en la otra dirección “\(\leq\)” entonces \(f\) es cóncava.
Geométricamente este resultado se ve como sigue para \(\nabla f(x) \neq 0\):
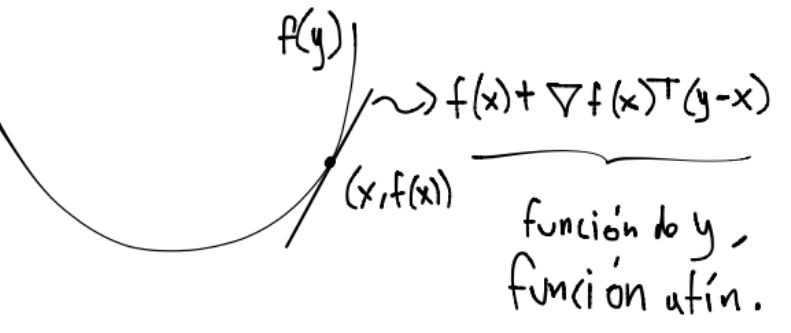
y el hiperplano \(f(x) + \nabla f(x)^T(y-x)\) se nombra hiperplano de soporte para la función \(f\) en el punto \((x,f(x))\). Obsérvese que si \(\nabla f(x)=0\) se tiene \(f(y) \geq f(x) \forall y \in \text{dom}f\) y por lo tanto \(x\) es un mínimo global de \(f\).
Una función es convexa si y sólo si es convexa al restringirla a cualquier línea que intersecte su dominio, esto es, si \(g(t) = f(x + tv)\) es convexa \(\forall x,v \in \mathbb{R}^n\), \(\forall t \in \mathbb{R}\) talque \(x + tv \in \text{dom}f\)
Sea \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) tal que \(f \in \mathcal{C}^2(\text{dom}f)\). Entonces \(f\) es convexa en \(\text{dom}f\) si y sólo si \(\text{dom}f\) es convexo y \(\nabla^2f(x) \in \mathbb{S}^n_+\) en \(\text{dom}f\). Si \(\nabla^2f(x) \in \mathbb{S}^n_{++}\) en \(\text{dom}f\) y \(\text{dom}f\) es convexo entonces \(f\) es estrictamente convexa en \(\text{dom}f\).
Comentario
Para una función: \(f: \mathbb{R} \rightarrow \mathbb{R}\), la hipótesis del enunciado anterior (\(\nabla^2 f(x) \in \mathbb{S}^n_{++}\) en \(\text{dom}f\)) es que la segunda derivada sea positiva. El recíproco no es verdadero, para ver esto considérese \(f(x)=x^4\) la cual es estrictamente convexa en \(\text{dom}f\) pero su segunda derivada en \(0\) no es positiva.
Sobre problemas de optimización#
Para problemas de optimización sin restricciones:
Condición necesaria de primer orden: si \(f_o\) es diferenciable y \(x^*\) es óptimo entonces \(\nabla f_o(x^*) = 0\).
Condición necesaria de segundo orden: si \(f_o \in \mathcal{C}^2(\text{domf})\) y \(x^*\) es mínimo local entonces \(\nabla^2 f_o(x^*) \in \mathbb{S}^n_{+}\)
Condición suficiente de segundo orden: si \(f_o \in \mathcal{C}^2(\text{domf})\), \(\nabla f_o(x)=0\) y \(\nabla^2f_o(x) \in \mathbb{S}^n_{++}\) entonces \(x\) es mínimo local estricto.
Comentario
Las condiciones anteriores se les conoce con el nombre de condiciones de optimalidad para problemas de optimización sin restricciones.
Sobre problemas de optimización convexa#
Una propiedad fundamental de un óptimo local en un problema de optimización convexa es que también es un óptimo global. Si la función es estrictamente convexa entonces el conjunto óptimo contiene a lo más un punto.
Si \(f_o\) es diferenciable y \(X\) es el conjunto de factibilidad entonces \(x\) es óptimo si y sólo si \(x \in X\) y \(\nabla f_o(x)^T(y-x) \geq 0\) \(\forall y \in X\). Si se considera como conjunto de factibilidad \(X = \text{dom}f_o\) (que es un problema sin restricciones) la propiedad se reduce a la condición necesaria y suficiente de primer orden: \(x\) es óptimo si y sólo si \(\nabla f_o(x) = 0\).
Geométricamente el resultado anterior se visualiza para \(\nabla f_o(x) \neq 0\) y \(-\nabla f_o(x)\) apuntando hacia la dirección dibujada:

Comentario
Por los resultados anteriores los métodos de optimización buscan resolver la ecuación no lineal \(\nabla f_o(x)=0\) para aproximar en general mínimos locales. Dependiendo del número de soluciones de la ecuación \(\nabla f_o(x)=0\) se tienen situaciones distintas. Por ejemplo, si no tiene solución entonces el/los óptimos no se alcanza(n) pues el problema puede no ser acotado por debajo o si existe el óptimo éste puede no alcanzarse. Por otro lado, si la ecuación tiene múltiples soluciones entonces cada solución es un mínimo de \(f_o\).
Sobre puntos críticos#
Definición
Puntos \(x \in \text{intdom}f\) en los que \(\nabla f(x) = 0\) o en los que \(\nabla f\) no existe, se les nombra puntos críticos o estacionarios de \(f\).
No todo punto crítico es un extremo de \(f\).
La Hessiana de \(f\) nos ayuda a caracterizar los puntos críticos en mínimos o máximos locales. Si \(x \in \mathbb{R}^n\) es punto crítico:
Y además \(\nabla^2f(x) \in \mathbb{S}_{++}\) entonces \(x\) es mínimo local.
Y además \(\nabla^2f(x) \in -\mathbb{S}_{++}\) entonces \(x\) es máximo local.
Y además \(\nabla^2f(x)\) es indefinida entonces \(x\) se nombra punto silla o saddle point.
Si \(x \in \mathbb{R}^n\) es punto crítico y \(\nabla^2f(x) \in \mathbb{S}_{+}\) no podemos concluir si es máximo o mínimo local (análogo si \(\nabla^2f(x) \in -\mathbb{S}_{+}\)).
Definición
Una matriz es indefinida si tiene eigenvalores positivos, negativos y cero.
Función fuertemente convexa#
Definición
Una función \(f:\mathbb{R}^n \rightarrow \mathbb{R}\) tal que \(f \in \mathcal{C}^2(\text{dom}f)\) se nombra fuertemente convexa en el conjunto convexo \(\mathcal{S} \neq \emptyset\) si existe \(m>0\) tal que \(\nabla^2 f(x) - mI\) es simétrica semidefinida positiva \(\forall x \in \mathcal{S}\).
Comentarios
Es equivalente escribir que una función \(f\) es fuertemente convexa en un conjunto \(\mathcal{S}\) que escribir qu la forma cuadrática que utiliza la matriz \(\nabla^2 f(x)\) está acotada por debajo por una cantidad positiva para toda \(x \in \mathcal{S}\) en la que se evalúe la forma cuadrática.
Por el punto anterior la función \(e^x\) no es fuertemente convexa pero sí estrictamente convexa (pensar en valores muy negativos). Asimismo \(-log(x)\) tampoco es fuertemente convexa pero sí estrictamente convexa (pensar en valores muy negativos o muy positivos).
La función \(x^2\) es fuertemente convexa y las formas cuadráticas definidas positivas también lo son.
Algunos resultados que son posibles probar para funciones fuertemente convexas#
Si una función es fuertemente convexa se puede probar que:
El conjunto óptimo contiene a lo más un punto.
\(f(y) \geq f(x) + \nabla f(x)^T(y-x) + \frac{m}{2}||y-x||_2^2 \forall x,y \in \mathcal{S}\), \(m > 0\). Por esto si \(f\) es fuertemente convexa en \(\mathcal{S}\) entonces es estrictamente convexa en \(\mathcal{S}\). También esta desigualdad indica que la diferencia entre la función de \(y\), \(f(y)\), y la función lineal en \(y\), \(f(x) + \nabla f(x)^T(y-x)\) (Taylor a primer orden), está acotada por debajo por una cantidad cuadrática.
Existe una cota superior para el número de condición bajo la norma 2 de la Hessiana de \(f\), esto es: \(\text{cond}(\nabla ^2 f(x))= \frac{\lambda_\text{max}(\nabla^2 f(x))}{\lambda_\text{min}(\nabla^2 f(x))} \leq K\) con \(K>0\), \(\forall x \in \mathcal{S}\).
La propiedad que una función sea fuertemente convexa garantiza que el número de condición de la Hessiana de \(f\) es una buena medida del desempeño de los algoritmos de optimización convexa sin restricciones (se revisará más adelante).
Observación
Si \(f\) es fuertemente convexa en \(\mathcal{S}\) entonces es estrictamente convexa en \(\mathcal{S}\) pero no viceversa, considérese por ejemplo \(f(x)=x^4\) la cual es estrictamente convexa en todo su dominio pero no es fuertemente convexa en todo su dominio pues su segunda derivada se anula en \(x=0\).
Preguntas de comprehensión.
1)Revisar el siguiente video: Ali Rahimi’s talk at NIPS de la plática de Ali Rahimi y la respuesta de Yann LeCun: My take on Ali Rahimi’s “Test of Time” award talk at NIPS.
2)Detalla qué es un problema de optimización matemática y describe sus elementos.
3)¿Qué forma tiene un problema estándar de optimización?
4)¿Qué propiedad tienen los problemas de optimización que nos ayuda a considerar únicamente problemas de minimización en el desarrollo de métodos y teoría para generalizarlos hacia los de maximización?
5)¿Qué propiedad cumple un punto que es óptimo para un problema de minimización?
6)¿Qué propiedad debe satisfacer una función para que se le llame convexa?
7)¿Qué forma tiene un problema convexo estándar con igualdades y desigualdades?
8)¿Cuál es la definición de un conjunto convexo?
9)Da ejemplos de conjuntos convexos.
10)¿Cuál es la definición de una combinación convexa?
11)Escribe equivalencias para definir funciones convexas.
12)¿Cuál es la definición de una función cóncava?
13)Escribe ejemplos de funciones convexas.
14)¿Cuál es la definición de una función estrictamente convexa?
15)Escribe resultados útiles respecto a problemas de optimización, optimización convexos y puntos críticos.
16)¿Cuál es la definición de una función fuertemente convexa?
Referencias:
S. P. Boyd, L. Vandenberghe, Convex Optimization, Cambridge University Press, 2009.

