2.1 Operaciones y transformaciones básicas del Álgebra Lineal Numérica

Notas para contenedor de docker:

Comando de docker para ejecución de la nota de forma local:

nota: cambiar <ruta a mi directorio> por la ruta de directorio que se desea mapear a /datos dentro del contenedor de docker y <versión imagen de docker> por la versión más actualizada que se presenta en la documentación.

docker run --rm -v <ruta a mi directorio>:/datos --name jupyterlab_optimizacion -p 8888:8888 -d palmoreck/jupyterlab_optimizacion:<versión imagen de docker>

password para jupyterlab: qwerty

Detener el contenedor de docker:

docker stop jupyterlab_optimizacion

Documentación de la imagen de docker palmoreck/jupyterlab_optimizacion:<versión imagen de docker> en liga.

---

Nota generada a partir de liga1, liga2 y liga3.

Al final de esta nota la comunidad lectora:

• Entenderá cómo utilizar transformaciones típicas en el álgebra lineal numérica en la que se basan muchos de los algoritmos del análisis numérico. En específico aprenderá cómo aplicar las transformaciones de Gauss, reflexiones de Householder y rotaciones Givens a vectores y matrices.

• Se familizarizará con la notación vectorial y matricial de las operaciones básicas del álgebra lineal numérica.

Las operaciones básicas del Álgebra Lineal Numérica podemos dividirlas en vectoriales y matriciales.

Vectoriales

• Transponer: \(\mathbb{R}^{n \times 1} \rightarrow \mathbb{R} ^{1 \times n}\): \(y = x^T\) entonces \(x = \left[ \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right ]\) y se tiene: \(y = x^T = [x_1, x_2, \dots, x_n].\)

• Suma: \(\mathbb{R}^n \times \mathbb{R} ^n \rightarrow \mathbb{R}^n\): \(z = x + y\) entonces \(z_i = x_i + y_i\)

• Multiplicación por un escalar: \(\mathbb{R} \times \mathbb{R} ^n \rightarrow \mathbb{R}^n\): \(y = \alpha x\) entonces \(y_i = \alpha x_i\).

• Producto interno estándar o producto punto: \(\mathbb{R}^n \times \mathbb{R} ^n \rightarrow \mathbb{R}\): \(c = x^Ty\) entonces \(c = \displaystyle \sum_{i=1}^n x_i y_i\).

• Multiplicación point wise: \(\mathbb{R}^n \times \mathbb{R} ^n \rightarrow \mathbb{R}^n\): \(z = x.*y\) entonces \(z_i = x_i y_i\).

• División point wise: \(\mathbb{R}^n \times \mathbb{R} ^n \rightarrow \mathbb{R}^n\): \(z = x./y\) entonces \(z_i = x_i /y_i\) con \(y_i \neq 0\).

• Producto exterior o outer product: \(\mathbb{R}^n \times \mathbb{R} ^n \rightarrow \mathbb{R}^{n \times n}\): \(A = xy^T\) entonces \(A[i, :] = x_i y^T\) con \(A[i,:]\) el \(i\)-ésimo renglón de \(A\).

Matriciales

• Transponer: \(\mathbb{R}^{m \times n} \rightarrow \mathbb{R}^{n \times m}\): \(C = A^T\) entonces \(c_{ij} = a_{ji}\).

• Sumar: \(\mathbb{R}^{m \times n} \times \mathbb{R}^{m \times n} \rightarrow \mathbb{R}^{m \times n}\): \(C = A + B\) entonces \(c_{ij} = a_{ij} + b_{ij}\).

• Multiplicación por un escalar: \(\mathbb{R} \times \mathbb{R}^{m \times n} \rightarrow \mathbb{R}^{m \times n}\): \(C = \alpha A\) entonces \(c_{ij} = \alpha a_{ij}\)

• Multiplicación por un vector: \(\mathbb{R}^{m \times n} \times \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\): \(y = Ax\) entonces \(y_i = \displaystyle \sum_{j=1}^n a_{ij}x_j\).

• Multiplicación entre matrices: \(\mathbb{R}^{m \times k} \times \mathbb{R}^{k \times n} \rightarrow \mathbb{R}^{m \times n}\): \(C = AB\) entonces \(c_{ij} = \displaystyle \sum_{r=1}^k a_{ir}b_{rj}\).

• Multiplicación point wise: \(\mathbb{R}^{m \times n} \times \mathbb{R}^{m \times n} \rightarrow \mathbb{R}^{m \times n}\): \(C = A.*B\) entonces \(c_{ij} = a_{ij}b_{ij}\).

• División point wise: \(\mathbb{R}^{m \times n} \times \mathbb{R}^{m \times n} \rightarrow \mathbb{R}^{m \times n}\): \(C = A./B\) entonces \(c_{ij} = a_{ij}/b_{ij}\) con \(b_{ij} \neq 0\).

Como ejemplos de transformaciones básicas del Álgebra Lineal Numérica se encuentran:

Transformaciones de Gauss

En esta sección suponemos que \(A \in \mathbb{R}^{n \times n}\) y \(A\) es una matriz con entradas \(a_{ij} \in \mathbb{R},\forall i,j=1,2,\dots,n\).

Como ejemplo de vector canónico tenemos: \(e_1=(1,0)^T\) en \(\mathbb{R}^2\) o \(e_3 = (0,0,1,0,0)^T\) en \(\mathbb{R}^5\).

Considérese al vector \(a \in \mathbb{R}^{n}\) y \(e_k \in \mathbb{R}^n\) el \(k\)-ésimo vector canónico: vector con un \(1\) en la posición \(k\) y ceros en las entradas restantes.

Definición

Una transformación de Gauss está definida de forma general como \(L_k = I_n - \ell_ke_k^T\) con \(\ell_k = (0,0,\dots,\ell_{k+1,k},\dots,\ell_{n,k})^T\) y \(\ell_{i,k}=\frac{a_{ik}}{a_{kk}} \forall i=k+1,\dots,n\).

\(a_{kk}\) se le nombra pivote y debe ser diferente de cero.

Las transformaciones de Gauss se utilizan para hacer ceros por debajo del pivote.

Ejemplo aplicando transformaciones de Gauss a un vector

Considérese al vector \(a=(-2,3,4)^T\). Definir una transformación de Gauss para hacer ceros por debajo de \(a_1\) y otra transformación de Gauss para hacer cero la entrada \(a_3\)

Solución:

import numpy as np
import math

np.set_printoptions(precision=3, suppress=True)

a)Para hacer ceros por debajo del pivote \(a_1 = -2\):

a = np.array([-2,3,4])

pivote = a[0]

Recuerda la definición de \(\ell_1=(0, \frac{a_2}{a_1}, \frac{a_3}{a_1})^T\)

l1 = np.array([0,a[1]/pivote, a[2]/pivote])

Usamos \(e_1\) pues se desea hacer ceros en las entradas debajo de la primera.

e1 = np.array([1,0,0])

Observa que por la definición de la transformación de Gauss, no necesitamos construir a la matriz \(L_1\), directamente se tiene \(L_1a = a - \ell_1 e_1^Ta\).

L1_a = a-l1*(e1.dot(a))

print(L1_a)

[-2.  0.  0.]

A continuación se muestra que el producto \(L_1 a\) si se construye \(L_1\) es equivalente a lo anterior:

\(L_1 = I_3 - \ell_1 e_1^T\).

L1 = np.eye(3) - np.outer(l1,e1)

print(L1)

[[1.  0.  0. ]
 [1.5 1.  0. ]
 [2.  0.  1. ]]

print(L1@a)

[-2.  0.  0.]

b) Para hacer ceros por debajo del pivote \(a_2 = 3\):

a = np.array([-2,3,4])

pivote = a[1]

Recuerda la definición de \(\ell_2=(0, 0, \frac{a_3}{a_2})^T\)

l2 = np.array([0,0, a[2]/pivote])

Usamos \(e_2\) pues se desea hacer ceros en las entradas debajo de la segunda.

e2 = np.array([0,1,0])

Observa que por la definición de la transformación de Gauss, no necesitamos construir a la matriz \(L_2\), directamente se tiene \(L_2a = a - \ell_2 e_2^Ta\).

L2_a = a-l2*(e2.dot(a))

print(L2_a)

[-2.  3.  0.]

A continuación se muestra que el producto \(L_2 a\) si se construye \(L_2\) es equivalente a lo anterior:

\(L_2 = I_3 - \ell_2 e_2^T\).

L2 = np.eye(3) - np.outer(l2,e2)

print(L2)

[[ 1.     0.     0.   ]
 [ 0.     1.     0.   ]
 [ 0.    -1.333  1.   ]]

print(L2@a)

[-2.  3.  0.]

Ejemplo aplicando transformaciones de Gauss a una matriz

Si tenemos una matriz \(A \in \mathbb{R}^{3 \times 3}\) y queremos hacer ceros por debajo de su diagonal y tener una forma triangular superior, realizamos los productos matriciales:

\[L_2 L_1 A\]

donde: \(L_1, L_2\) son transformaciones de Gauss.

Posterior a realizar el producto \(L_2 L_1 A\) se obtiene una matriz triangular superior:

\[\begin{split} L_2L_1A = \left [ \begin{array}{ccc} * & * & *\\ 0 & * & * \\ 0 & 0 & *  \end{array} \right ] \end{split}\]

Ejemplo:

a) Utilizando \(L_1\)

A = np.array([[-1, 2, 5],
              [4, 5, -7],
              [3, 0, 8]], dtype=float)

print(A)

[[-1.  2.  5.]
 [ 4.  5. -7.]
 [ 3.  0.  8.]]

Para hacer ceros por debajo del pivote \(a_{11} = -1\):

pivote = A[0, 0]

Recuerda la definición de \(\ell_1=(0, \frac{a_{21}}{a_{11}}, \frac{a_{31}}{a_{11}})^T\)

l1 = np.array([0,A[1,0]/pivote, A[2,0]/pivote])

print(l1)

[ 0. -4. -3.]

e1 = np.array([1,0,0])

Observa que por la definición de la transformación de Gauss, no necesitamos construir a la matriz \(L_1\), directamente se tiene \(L_1 A[1:3,1] = A[1:3,1] - \ell_1 e_1^T A[1:3,1]\).

L1_A_1 = A[:,0]-l1*(e1.dot(A[:,0]))

print(L1_A_1)

[-1.  0.  0.]

Y se debe aplicar \(L_1\) a las columnas número 2 y 3 de \(A\) para completar el producto \(L_1A\):

Aplicando \(L_1\) a la segunda columna de \(A\): \(A[1:3,2]\).

L1_A_2 = A[:,1]-l1*(e1.dot(A[:,1]))

print(L1_A_2)

[ 2. 13.  6.]

Aplicando \(L_1\) a la tercer columna de \(A\): \(A[1:3,3]\).

L1_A_3 = A[:,2]-l1*(e1.dot(A[:,2]))

print(L1_A_3)

[ 5. 13. 23.]

A continuación se muestra que el producto \(L_1 A\) si se construye \(L_1\) es equivalente a lo anterior:

\(L_1 = I_3 - \ell_1 e_1^T\).

L1 = np.eye(3) - np.outer(l1,e1)

print(L1)

[[1. 0. 0.]
 [4. 1. 0.]
 [3. 0. 1.]]

print(L1 @ A)

[[-1.  2.  5.]
 [ 0. 13. 13.]
 [ 0.  6. 23.]]

Observación

Al aplicar \(L_1\) a la primer columna de \(A\) siempre obtenemos ceros por debajo del pivote que en este caso es \(a_{11}\).

A continuación se muestra cómo aplicar el producto \(L_1 A\) para la segunda y tercer columna de \(A\) utilizando un outer product.

Después de hacer la multiplicación \(L_1A\) en cualquiera de los dos casos (construyendo o no explícitamente \(L_1\)) no se modifica el primer renglón de \(A\):

print(A)

[[-1.  2.  5.]
 [ 4.  5. -7.]
 [ 3.  0.  8.]]

Este es el primer renglón de \(A\).

print(A[0,:])

[-1.  2.  5.]

Tomando el primer renglón del producto \(L_1A\).

print((L1 @ A)[0,:])

[-1.  2.  5.]

por lo que la multiplicación \(L_1A\) entonces modifica del segundo renglón de \(A\) en adelante y de la segunda columna de \(A\) en adelante.

Observación

Dada la forma de \(L_1 = I_3 - \ell_1e_1^T\), si primero sólo consideramos \(e_1^T\) de la expresión anterior, al hacer la multiplicación por la segunda y tercer columna de \(A\) se tiene:

\[e_1^T A[1:3,2] = A[0,2]\]

\[e_1^T A[1:3,3] = A[0,3]\]

respectivamente.

El resultado de este producto es un escalar.

print(e1.dot(A[:, 1]))

2.0

El resultado de este producto es un escalar.

print(e1.dot(A[:, 2]))

5.0

y puede escribirse de forma compacta:

\[e_1^T A[1:3,2:3] = A[0, 2:3]\]

print(A[0, 1:3]) #observe that we have to use 2+1=3 as the second number after ":" in 1:3

[2. 5.]

print(A[0, 1:]) #also we could have use this statement

[2. 5.]

Entonces los productos \(\ell_1 e_1^T A[1 : 3,2]\) y \(\ell_1 e_1^T A[1 :3 ,3]\) quedan respectivamente como:

\[\ell_1A[0, 2]\]

print(l1*A[0, 1])

[ 0. -8. -6.]

\[\ell_1A[0,3]\]

print(l1*A[0, 2])

[  0. -20. -15.]

Observación

En los dos cálculos anteriores, las primeras entradas son iguales a \(0\) por lo que es consistente con el hecho que únicamente se modifican dos entradas de la segunda y tercer columna de \(A\).

De forma compacta y aprovechando funciones en NumPy como np.outer se puede calcular lo anterior como:

print(np.outer(l1[1:3],A[0,1:3]))

[[ -8. -20.]
 [ -6. -15.]]

print(np.outer(l1[1:],A[0,1:])) #also we could have use this statement

[[ -8. -20.]
 [ -6. -15.]]

Recuerda que:

print(l1[1:3])

[-4. -3.]

y

print(A[0, 1:3])

[2. 5.]

Finalmente la aplicación de \(L_1\) al segundo renglón y segunda columna en adelante de \(A\) queda:

Observa que por la definición de la transformación de Gauss, no necesitamos construir a la matriz \(L_1\), directamente se tiene \(L_1 A = A - \ell_1 e_1^T A\) y podemos aprovechar lo anterior para sólo operar de la segunda columna y segundo renglón en adelante.

print(A[1:, 1:] - np.outer(l1[1:],A[0,1:]))

[[13. 13.]
 [ 6. 23.]]

Compárese con:

print(L1 @ A)

[[-1.  2.  5.]
 [ 0. 13. 13.]
 [ 0.  6. 23.]]

Entonces sólo falta colocar el primer renglón y primera columna al producto. Para esto combinamos columnas y renglones en numpy con column_stack y row_stack:

A_aux = A[1:, 1:] - np.outer(l1[1:],A[0,1:])

m, n = A.shape
number_of_zeros = m-1
A_aux_2 = np.column_stack((np.zeros(number_of_zeros), A_aux)) # stack two zeros

print(A_aux_2)

[[ 0. 13. 13.]
 [ 0.  6. 23.]]

A_aux_3 = np.row_stack((A[0, :], A_aux_2))

print(A_aux_3)

[[-1.  2.  5.]
 [ 0. 13. 13.]
 [ 0.  6. 23.]]

que es el resultado de:

print(L1 @ A)

[[-1.  2.  5.]
 [ 0. 13. 13.]
 [ 0.  6. 23.]]

O bien:

A[:,0:]-np.outer(l1,e1.dot(A[:,0:]))

array([[-1.,  2.,  5.],
       [ 0., 13., 13.],
       [ 0.,  6., 23.]])

Lo que falta para obtener una matriz triangular superior es hacer la multiplicación \(L_2L_1A\). Para este caso la matriz \(L_2=I_3 - \ell_2e_2^T\) utiliza \(\ell_2 = \left( 0, 0, \frac{a^{(1)}_{32}}{a^{(1)}_{22}} \right )^T\) donde: \(a^{(1)}_{ij}\) son las entradas de \(A^{(1)} = L_1A^{(0)}\) y \(A^{(0)}=A\).

Ejercicio

Utilizando lenguajes de programación calcular el producto \(L_2 L_1 A\) para la matriz anterior y para la matriz:

\[\begin{split} A = \left [ \begin{array}{ccc} 1 & 4 & -2 \\ -3 & 9 & 8 \\ 5 & 1 & -6 \end{array} \right] \end{split}\]

tomando en cuenta que en este caso \(L_2\) sólo opera del segundo renglón y segunda columna en adelante:

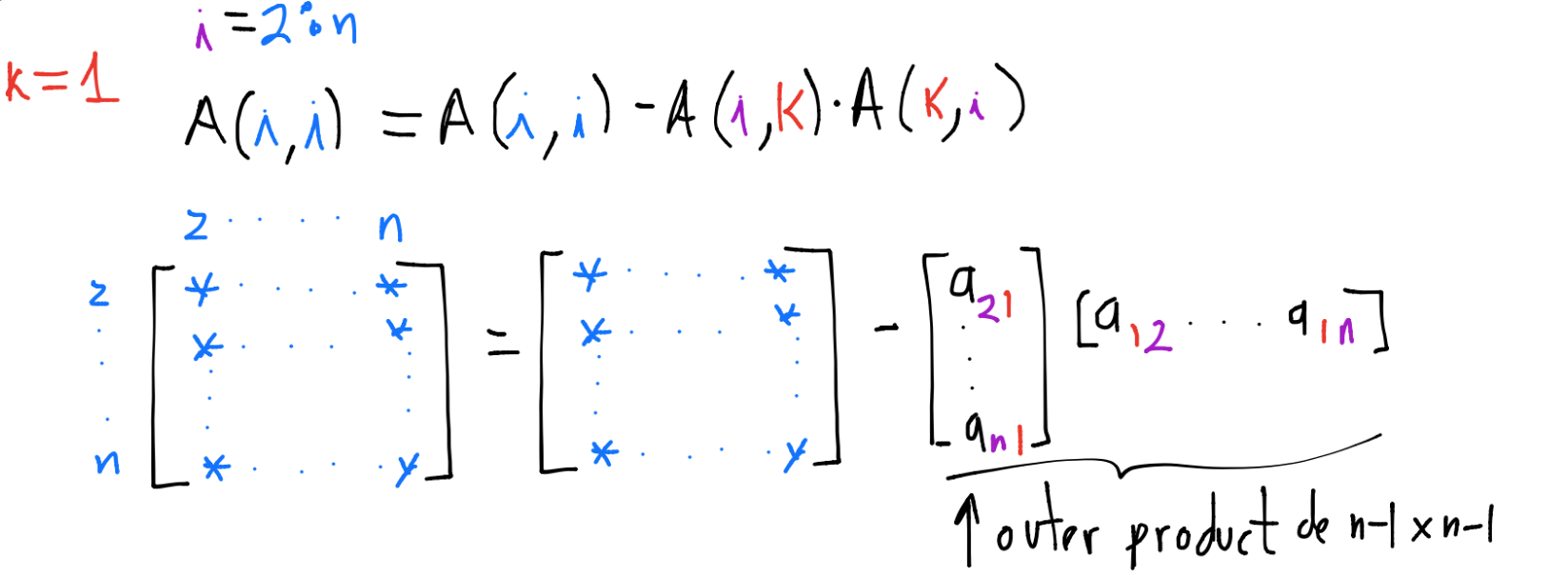
y obtener una matriz triangular superior en cada ejercicio.

Comentarios

• Las transformaciones de Gauss se utilizan para la fase de eliminación del método de eliminación Gaussiana o también llamada factorización \(LU\). Ver Gaussian elimination.

• La factorización \(P, L, U\) que es la \(LU\) con permutaciones por pivoteo parcial es un método estable numéricamente respecto al redondeo en la práctica pero inestable en la teoría.

Matriz ortogonal y matriz con columnas ortonormales

Un conjunto de vectores \(\{x_1, \dots, x_p\}\) en \(\mathbb{R}^m\) (\(x_i \in \mathbb{R}^m\))es ortogonal si \(x_i^Tx_j=0\) \(\forall i\neq j\). Por ejemplo, para un conjunto de \(2\) vectores \(x_1,x_2\) en \(\mathbb{R}^3\) esto se visualiza:

Comentarios

• Si el conjunto \(\{x_1,\dots,x_n\}\) en \(\mathbb{R}^m\) satisface \(x_i^Tx_j= \delta_{ij}= \begin{cases} 1 &\text{ si } i=j,\\ 0 &\text{ si } i\neq j \end{cases}\), ver Kronecker_delta se le nombra conjunto ortonormal, esto es, constituye un conjunto ortogonal y cada elemento del conjunto tiene norma \(2\) o Euclidiana igual a \(1\): \(||x_i||_2 = 1, \forall i=1,\dots,n\).

  • Si definimos a la matriz \(X\) con columnas dadas por cada uno de los vectores del conjunto \(\{x_1,\dots, x_n\}\): \(X=(x_1, \dots , x_n) \in \mathbb{R}^{m \times n}\) entonces la propiedad de que cada par de columnas satisfaga \(x_i^Tx_j=\delta_{ij}\) se puede escribir en notación matricial como \(X^TX = I_n\) con \(I_n\) la matriz identidad de tamaño \(n\) si \(n \leq m\) o bien \(XX^T=I_m\) si \(m \leq n\). A la matriz \(X\) se le nombra matriz con columnas ortonormales.

  • Si cada \(x_i\) está en \(\mathbb{R}^n\) (en lugar de \(\mathbb{R}^m\)) entonces construímos a la matriz \(X\) como el punto anterior con la diferencia que \(X \in \mathbb{R}^{n \times n}\). En este caso \(X\) se le nombra matriz ortogonal.

• Entre las propiedades más importantes de las matrices ortogonales o con columnas ortonormales es que son isometrías bajo la norma \(2\) o Euclidiana y multiplicar por tales matrices es estable numéricamente bajo el redondeo, ver Condición de un problema y estabilidad de un algoritmo.

Transformaciones de reflexión

En esta sección suponemos que \(A \in \mathbb{R}^{m \times n}\) y \(A\) es una matriz con entradas \(a_{ij} \in \mathbb{R}, \forall i=1,2,\dots,m, j=1, 2, \dots, n\).

Reflectores de Householder

Recuerda que \(u^\perp = \{x \in \mathbb{R}^m| u^Tx=0\}\) es un subespacio de \(\mathbb{R}^m\) de dimensión \(m-1\) y es el complemento ortogonal de \(u\).

Definición

Las reflexiones de Householder son matrices simétricas, ortogonales y se construyen a partir de un vector \(v \neq 0\) definiendo:

\[R_H = I_m-\beta v v^T\]

con \(v \in \mathbb{R}^m - \{0\}\) y \(\beta = \frac{2}{v^Tv}\). El vector \(v\) se llama vector de Householder. La multiplicación \(R_Hx\) representa la reflexión del vector \(x \in \mathbb{R}^m\) a través del hiperplano \(v^\perp\).

Comentario

Algunas propiedades de las reflexiones de Householder son: \(R_H^TR_H = R_H^2 = I_m\), \(R_H^{-1}=R_H\), \(det(R_H)=-1\).

Proyector ortogonal elemental

En este dibujo se utiliza el proyector ortogonal elemental sobre el complemento ortogonal \(u^\perp\) definido como: \(P=I_m- u u^T\) y \(Px\) es la proyección ortogonal de \(x\) sobre \(u^\perp\) . Los proyectores ortogonales elementales no son matrices ortogonales, son singulares, son simétricas y \(P^2=P\). El proyector ortogonal elemental de \(x\) sobre \(u^\perp\) tienen \(rank\) igual a \(m-1\) y el proyector ortogonal de \(x\) sobre \(span\{u\}\) definido por \(I_m-P=uu^T\) tienen \(rank\) igual a \(1\).

Recuerda que \(span\{u\}\) es el conjunto generado por \(u\). Se define como el conjunto de combinaciones lineales de \(u\): \(span\{u\} = \left \{k u | k \in \mathbb{R} \forall i =1,\dots,m \right \}\).

Un dibujo que ayuda a visualizar el reflector elemental alrededor de \(u^\perp\) en el que se utiliza \(u \in \mathbb{R}^m - \{0\}\) , \(||u||_2 = 1\) y \(R_H=I_m-2 u u^T\) es el siguiente :

Las reflexiones de Householder pueden utilizarse para hacer ceros por debajo de una entrada de un vector.

Ejemplo aplicando reflectores de Householder a un vector

Considérese al vector \(x=(1,2,3)^T\). Definir un reflector de Householder para hacer ceros por debajo de \(x_1\).

x = np.array([1,2,3])

print(x)

[1 2 3]

Utilizamos la definición \(v=x-||x||_2e_1\) con \(e_1=(1,0,0)^T\) vector canónico para construir al vector de Householder:

Usamos \(e_1\) pues se desea hacer ceros en las entradas debajo de la primera.

e1 = np.array([1,0,0]) 
v = x-np.linalg.norm(x)*e1

Recuerda la definición de \(\beta = \frac{2}{v^Tv}\) para \(v\) no unitario.

beta = 2/v.dot(v)

Observa que por la definición de la reflexión de Householder, no necesitamos construir a la matriz \(R_H\), directamente se tiene \(R_H x = x - \beta vv^Tx\).

Hacemos ceros por debajo de la primera entrada de \(x\) haciendo la multiplicación matriz-vector \(R_Hx\):

print(x-beta*v*(v.dot(x)))

[3.742 0.    0.   ]

El resultado de \(R_Hx\) es \((||x||_2,0,0)^T\) con \(||x||_2\) dada por:

print(np.linalg.norm(x))

3.7416573867739413

Observación

• Observa que se preserva la norma \(2\) o Euclidiana del vector, las matrices de reflexión de Householder son matrices ortogonales y por tanto isometrías: \(||R_Hv||_2=||v||_2\).

• Observa que a diferencia de las transformaciones de Gauss con las reflexiones de Householder en general se modifica la primera entrada, ver Ejemplo aplicando transformaciones de Gauss a un vector.

A continuación se muestra que el producto \(R_Hx\) si se construye \(R_H\) es equivalente a lo anterior:

\(R_H = I_3 - \beta v v^T\).

R_H = np.eye(3)-beta*np.outer(v,np.transpose(v))

print(R_H)

[[ 0.267  0.535  0.802]
 [ 0.535  0.61  -0.585]
 [ 0.802 -0.585  0.123]]

print(R_H@x)

[3.742 0.    0.   ]

Ejemplo aplicando reflectores de Householder a un vector

Considérese al mismo vector \(x\) del ejemplo anterior y el mismo objetivo “Definir un reflector de Householder para hacer ceros por debajo de \(x_1\)”. Otra opción para construir al vector de Householder es \(v=x+||x||_2e_1\) con \(e_1=(1,0,0)^T\) vector canónico:

Usamos \(e_1\) pues se desea hacer ceros en las entradas debajo de la primera.

e1 = np.array([1,0,0])
v = x+np.linalg.norm(x)*e1

Recuerda la definición de \(\beta = \frac{2}{v^Tv}\) para \(v\) no unitario.

beta = 2/v.dot(v)

Observa que por la definición de la reflexión de Householder, no necesitamos construir a la matriz \(R_H\), directamente se tiene \(R_H x = x - \beta vv^Tx\).

Hacemos ceros por debajo de la primera entrada de \(x\) haciendo la multiplicación matriz-vector \(R_Hx\):

print(x-beta*v*(v.dot(x)))

[-3.742 -0.    -0.   ]

Observación

Observa que difieren en signo las primeras entradas al utilizar \(v=x + ||x||_2 e_1\) o \(v=x - ||x||_2 e_1\).

¿Cuál definición del vector de Householder usar?

En cualquiera de las dos definiciones del vector de Householder \(v=x \pm ||x||_2 e_1\), la multiplicación \(R_Hx\) refleja \(x\) en el primer eje coordenado (pues se usa \(e_1\)):

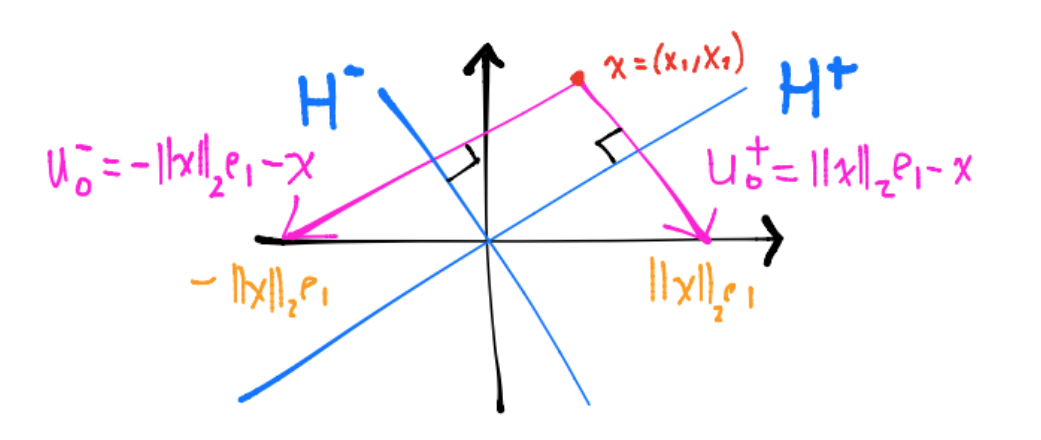
El vector \(v^+ = - u_0^+ = x-||x||_2e_1\) se utiliza para construir la transformación de Householder que refleja \(x\) respecto al subespacio \(H^+\) (que en el dibujo es una recta que cruza el origen). Análogamente se tiene una situación similar con el vector \(v^- = -u_0^- = x+||x||_2e_1\) y el subespacio \(H^-\).

Para reducir los errores por redondeo y evitar el problema de cancelación en la aritmética de punto flotante (ver Sistema de punto flotante) se utiliza:

\[v = x+signo(x_1)||x||_2e_1\]

donde: \(signo(x_1) = \begin{cases} 1 &\text{ si } x_1 \geq 0 ,\\ -1 &\text{ si } x_1 < 0 \end{cases}.\)

La idea de la definción anterior con la función \(signo(\cdot)\) es que la reflexión (en el dibujo anterior \(-||x||_2e_1\) o \(||x||_2e_1\)) sea lo más alejada posible de \(x\). En el dibujo anterior como \(x_1, x_2>0\) entonces se refleja respecto al subespacio \(H^-\) quedando su reflexión igual a \(-||x||_2e_1\).

Comentarios

• Otra forma de lidiar con el problema de cancelación es definiendo a la primera componente del vector de Householder \(v_1\) como \(v_1=x_1-||x||_2\) y haciendo una manipulación algebraica como sigue:

\[v_1=x_1-||x||_2 = \frac{x_1^2-||x||_2^2}{x_1+||x||_2} = -\frac{x_2^2+x_3^2+\dots + x_m^2}{x_1+||x||_2}.\]

• En la implementación del cálculo del vector de Householder, es útil que \(v_1=1\) y así únicamente se almacenará \(v[2:m]\). Al vector \(v[2:m]\) se le nombra parte esencial del vector de Householder.

• Las transformaciones de reflexión de Householder se utilizan para la factorización QR. Ver QR decomposition, la cual es una factorización estable numéricamente bajo el redondeo.

Ejercicio

Utilizando lenguajes de programación reflejar al vector \(v=\left [\begin{array}{c}1 \\1 \\\end{array}\right ]\) utilizando al vector de Householder \(u = \left [\begin{array}{c}\frac{-4}{3}\\\frac{2}{3}\end{array}\right ]\) para construir \(R_H\). Graficar \(v, u, u^\perp\) y el vector reflejado.

Ejemplo aplicando reflectores de Householder a una matriz

Las reflexiones de Householder se utilizan para hacer ceros por debajo de la diagonal a una matriz y tener una forma triangular superior (mismo objetivo que las transformaciones de Gauss, ver Ejemplo aplicando transformaciones de Gauss a una matriz). Por ejemplo si se han hecho ceros por debajo del elemento \(a_{11}\) y se quieren hacer ceros debajo de \(a_{22}^{(1)}\):

\[\begin{split}\begin{array}{l} R_2A^{(1)} = R_2 \left[ \begin{array}{cccc} * & * & * & *\\ 0 & * & * & *\\ 0 & * & * & * \\ 0 & * & * & * \\ 0 & * & * & * \end{array} \right] = \left[ \begin{array}{cccc} * & * & * & *\\ 0 & * & * & *\\ 0 & 0 & * & * \\ 0 & 0 & * & * \\ 0 & 0 & * & * \end{array} \right] := A^{(2)} \end{array} \end{split}\]

donde: \(a^{(1)}_{ij}\) son las entradas de \(A^{(1)} = R_1A^{(0)}\) y \(A^{(0)}=A\), \(R_1\) es matriz de reflexión de Householder.

En este caso

\[\begin{split}R_2 = \left [ \begin{array}{cc} 1 & 0 \\ 0 & \hat{R_2} \end{array} \right ] \end{split}\]

con \(\hat{R}_2\) una matriz de reflexión de Householder que hace ceros por debajo de de \(a_{22}^{(1)}\). Se tienen las siguientes propiedades de \(R_2\):

• No modifica el primer renglón de \(A^{(1)}\).

• No destruye los ceros de la primer columna de \(A^{(1)}\).

• \(R_2\) es una matriz de reflexión de Householder.

Observación

Para la implementación computacional no se inserta \(\hat{R}_2\) en \(R_2\), en lugar de esto se aplica \(\hat{R}_2\) a la submatriz \(A^{(1)}[2:m, 2:m]\).

Considérese a la matriz \(A \in \mathbb{R}^{4 \times 3}\):

\[\begin{split}A = \left [ \begin{array}{ccc} 3 & 2 & -1 \\ 2 & 3 & 2 \\ -1 & 2 & 3 \\ 2 & 1 & 4 \end{array} \right ] \end{split}\]

y aplíquense reflexiones de Householder para llevarla a una forma triangular superior.

A = np.array([[3 ,2, -1],
              [2 ,3 ,2],
              [-1, 2 ,3],
              [2 ,1 ,4]], dtype = float)

print(A)

[[ 3.  2. -1.]
 [ 2.  3.  2.]
 [-1.  2.  3.]
 [ 2.  1.  4.]]

Usamos \(e_1\) pues se desea hacer ceros en las entradas debajo de la primera entrada de la primera columna de \(A\): \(A[1:4,1]\).

e1 = np.array([1,0,0,0])

Recuerda la definición de \(v= A[1:4,1] + signo(A[1,1])||A[1:4,1]||_2e_1\).

v = A[:,0] + np.linalg.norm(A[:,0])*e1

print(v)

[ 7.243  2.    -1.     2.   ]

Recuerda la definición de \(\beta = \frac{2}{v^Tv}\) para \(v\) no unitario.

beta = 2/v.dot(v)

print(beta)

0.032543690979272503

La siguiente lista la utilizamos para guardar a las partes esenciales del vector de Householder y las betas:

l_betas = []
l_v_Householder = []

l_betas.append(beta)
l_v_Householder.append(v)

Observa que por la definición de la reflexión de Householder, no necesitamos construir a la matriz \(R_1\), directamente se tiene \(R_1 A[1:4,1] = A[1:4,1] - \beta vv^TA[1:4,1]\).

print(A[:,0] - beta*v*v.dot(A[:,0]))

[-4.243 -0.     0.    -0.   ]

Recuerda \(A^{(1)} = R_1 A^{(0)}\).

A1 = A[:,0:]-beta*np.outer(v,v.dot(A[:,0:]))

print(A1)

[[-4.243 -2.828 -1.414]
 [-0.     1.667  1.886]
 [ 0.     2.667  3.057]
 [-0.    -0.333  3.886]]

Observación

Observa que a diferencia de las transformaciones de Gauss la reflexión de Householder \(R_1\) sí modifica el primer renglón de \(A^{(0)}\), ver Después de hacer la multiplicación….

Se preserva la norma \(2\) o Euclidiana de \(A[1:4,1]\).

print(np.linalg.norm(A1[:,0]))

4.2426406871192865

print(np.linalg.norm(A[:,0]))

4.242640687119285

A continuación queremos hacer ceros debajo de la segunda entrada de la segunda columna de \(A^{(1)}\).

Usamos \(e_1\) pues se desea hacer ceros en las entradas debajo de la segunda entrada de la segunda columna de \(A^{(1)}\): \(A^{(1)}[2:4,2]\).

e1 = np.array([1, 0, 0])

Recuerda la definición de \(v= A[2:4,2] + signo(A[2,2])||A[2:4,2]||_2e_1\).

v = A1[1:,1] + np.linalg.norm(A1[1:,1])*e1

print(v)

[ 4.829  2.667 -0.333]

Recuerda la definición de \(\beta = \frac{2}{v^Tv}\) para \(v\) no unitario.

beta = 2/v.dot(v)

l_betas

[0.032543690979272503]

l_v_Householder

[array([ 7.243,  2.   , -1.   ,  2.   ])]

l_betas.append(beta)
l_v_Householder.append(v)

Observa que por la definición de la reflexión de Householder, no necesitamos construir a la matriz \(R_2\), directamente se tiene \(R_2A[2:4,2] = A[2:4,2] - \beta vv^TA[2:4,2]\).

print(A1[1:,1] - beta*v*v.dot(A1[1:,1]))

[-3.162  0.     0.   ]

Recuerda \(A^{(2)} = R_2 A^{(1)}\) pero sólo operamos en \(A^{(2)}[2:4, 2:3]\).

A2_aux = A1[1:,1:]-beta*np.outer(v,v.dot(A1[1:,1:]))

print(A2_aux)

[[-3.162 -3.162]
 [ 0.     0.27 ]
 [ 0.     4.234]]

Se preserva la norma \(2\) o Euclidiana de \(A[2:4,2]\).

print(np.linalg.norm(A1[1:,1]))

3.1622776601683795

A continuación queremos hacer ceros debajo de la tercera entrada de la tercera columna de \(A^{(2)}\).

e1 = np.array([1, 0])

v = A2_aux[1:,1] + np.linalg.norm(A2_aux[1:,1])*e1

print(v)

[4.512 4.234]

beta = 2/v.dot(v)

l_betas.append(beta)
l_v_Householder.append(v)

Recuerda \(A^{(3)} = R_3 A^{(2)}\) pero sólo operamos en \(A^{(2)}[3:4, 3]\).

A3_aux = A2_aux[1:,1]-beta*v*v.dot(A2_aux[1:,1])

print(A3_aux)

[-4.243  0.   ]

print(np.linalg.norm(A2_aux[1:,1]))

4.242640687119285

Entonces sólo falta colocar los renglones y columnas para tener a la matriz \(A^{(3)}\). Para esto combinamos columnas y renglones en numpy con column_stack y row_stack:

m,n = A.shape

number_of_zeros = m-2

A3_aux_2 = np.column_stack((np.zeros(number_of_zeros), A3_aux)) 

print(A3_aux_2)

[[ 0.    -4.243]
 [ 0.     0.   ]]

A3_aux_3 = np.row_stack((A2_aux[0, 0:], A3_aux_2))

print(A3_aux_3)

[[-3.162 -3.162]
 [ 0.    -4.243]
 [ 0.     0.   ]]

number_of_zeros = m-1

A3_aux_4 = np.column_stack((np.zeros(number_of_zeros), A3_aux_3)) 

print(A3_aux_4)

[[ 0.    -3.162 -3.162]
 [ 0.     0.    -4.243]
 [ 0.     0.     0.   ]]

La matriz \(A^{(3)} = R_3 R_2 R_1 A^{(0)}\) es:

A3 = np.row_stack((A1[0, 0:], A3_aux_4))

print(A3)

[[-4.243 -2.828 -1.414]
 [ 0.    -3.162 -3.162]
 [ 0.     0.    -4.243]
 [ 0.     0.     0.   ]]

Podemos verificar lo anterior comparando con la matriz \(R\) de la factorización \(QR\) de \(A\):

q,r = np.linalg.qr(A)
print("Q:")
print(q)
print("R:")
print(r)

Q:
[[-0.707  0.     0.471]
 [-0.471 -0.527  0.079]
 [ 0.236 -0.843 -0.157]
 [-0.471  0.105 -0.864]]
R:
[[-4.243 -2.828 -1.414]
 [ 0.    -3.162 -3.162]
 [ 0.     0.    -4.243]]

Ejercicio

Utilizando lenguajes de programación aplicar reflexiones de Householder a la matriz

\[\begin{split}A = \left [ \begin{array}{cccc} 4 & 1 & -2 & 2 \\ 1 & 2 & 0 & 1\\ -2 & 0 & 3 & -2 \\ 2 & 1 & -2 & -1 \end{array} \right ] \end{split}\]

para obtener una matriz triangular superior.

Cálculo del factor \(Q\) en la factorización \(QR\) con reflexiones de Householder

Con los vectores de Householder puede construirse el factor \(Q\) para la factorización \(QR\) utilizando el producto:

\[Q = R_1 R_2 \cdots R_n\]

donde: \(R_i \in \mathbb{R}^{m \times m}\) es reflexión de Householder.

Observación

Un mejor uso de almacenamiento es utilizar las partes esenciales de los vectores de Householder.

En el caso del ejemplo anterior utilizamos las listas:

print(l_betas)

[0.032543690979272503, 0.06548590014996047, 0.05223603090473924]

print(l_v_Householder)

[array([ 7.243,  2.   , -1.   ,  2.   ]), array([ 4.829,  2.667, -0.333]), array([4.512, 4.234])]

Q_Householder = np.eye(m)

for j in range(n-1,-1,-1):
    v = l_v_Householder[j]
    Q_Householder[j:m, j:m] = Q_Householder[j:m, j:m] - l_betas[j]*np.outer(v, v.dot(Q_Householder[j:m,j:m]))

print(Q_Householder)

[[-0.707  0.     0.471 -0.527]
 [-0.471 -0.527  0.079  0.703]
 [ 0.236 -0.843 -0.157 -0.457]
 [-0.471  0.105 -0.864 -0.141]]

Podemos verificar lo anterior comparando con la matriz \(Q\) de la factorización \(QR\) de \(A\):

q,r = np.linalg.qr(A, "complete")
print("Q:")
print(q)
print("R:")
print(r)

Q:
[[-0.707  0.     0.471 -0.527]
 [-0.471 -0.527  0.079  0.703]
 [ 0.236 -0.843 -0.157 -0.457]
 [-0.471  0.105 -0.864 -0.141]]
R:
[[-4.243 -2.828 -1.414]
 [ 0.    -3.162 -3.162]
 [ 0.     0.    -4.243]
 [ 0.     0.     0.   ]]

Transformaciones de rotación

En esta sección suponemos que \(A \in \mathbb{R}^{m \times n}\) y \(A\) es una matriz con entradas \(a_{ij} \in \mathbb{R}\forall i=1,2,\dots,m, j=1, 2, \dots, n\).

Si \(u, v \in \mathbb{R}^2-\{0\}\) con \(\ell = ||u||_2 = ||v||_2\) y se desea rotar al vector \(u\) en sentido contrario a las manecillas del reloj por un ángulo \(\theta\) para llevarlo a la dirección de \(v\):

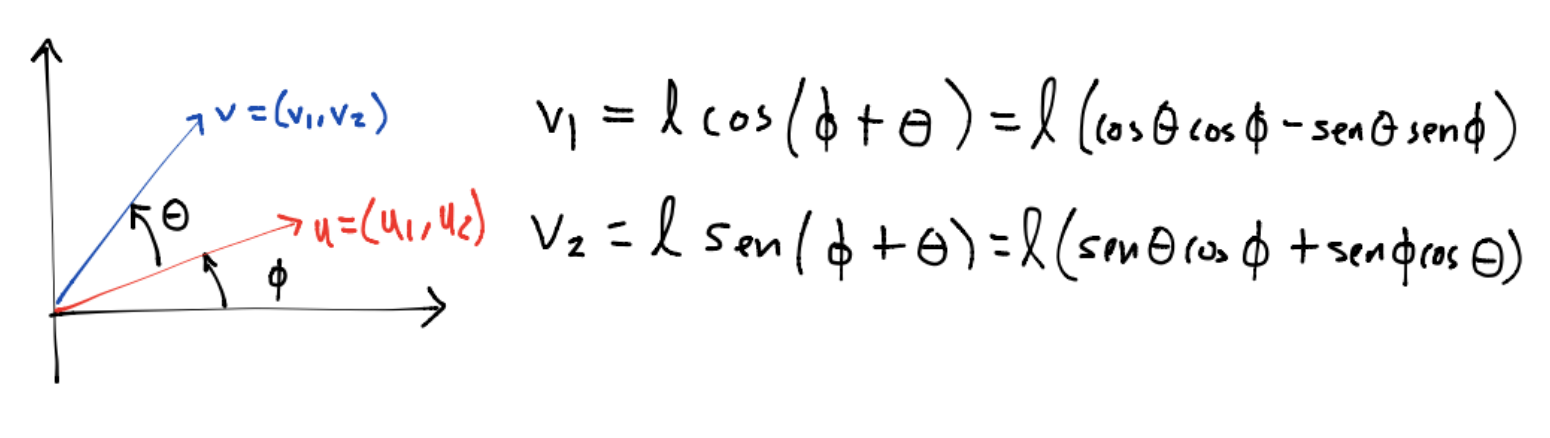
A partir de las relaciones anteriores como \(cos(\phi)=\frac{u_1}{\ell}, sen(\phi)=\frac{u_2}{\ell}\) se tiene: \(v_1 = (cos\theta)u_1-(sen\theta)u_2\), \(v_2=(sen\theta)u_1+(cos\theta)u_2\) equivalentemente:

\[\begin{split}\begin{array}{l} \left[\begin{array}{c} v_1\\ v_2 \end{array} \right] = \left[ \begin{array}{cc} cos\theta & -sen\theta\\ sen\theta & cos\theta \end{array} \right] \cdot \left[\begin{array}{c} u_1\\ u_2 \end{array} \right] \end{array} \end{split}\]

Definición

La matriz \(R_O\):

\[\begin{split}R_O= \left[ \begin{array}{cc} cos\theta & -sen\theta\\ sen\theta & cos\theta \end{array} \right] \end{split}\]

se nombra matriz de rotación o rotaciones Givens, es una matriz ortogonal pues \(R_O^TR_O=I_2\).

La multiplicación \(v=R_Ou\) es una rotación en sentido contrario a las manecillas del reloj, de hecho cumple \(det(R_O)=1\). La multiplicación \(u=R_O^Tv\) es una rotación en sentido de las manecillas del reloj y el ángulo asociado es \(-\theta\).

Ejemplo aplicando rotaciones Givens a un vector

Rotar al vector \(v=(1,1)^T\) un ángulo de \(45^o\) en sentido contrario a las manecillas del reloj.

v=np.array([1,1])

La matriz \(R_O\) es:

\[\begin{split}R_O = \left[ \begin{array}{cc} cos(\frac{\pi}{4}) & -sen(\frac{\pi}{4})\\ sen(\frac{\pi}{4}) & cos(\frac{\pi}{4}) \end{array} \right ] \end{split}\]

theta=math.pi/4
R_O=np.array([[math.cos(theta), -math.sin(theta)],
               [math.sin(theta), math.cos(theta)]])

print(R_O)

[[ 0.707 -0.707]
 [ 0.707  0.707]]

print(R_O@v)

[0.    1.414]

print(np.linalg.norm(v))

1.4142135623730951

Observación

Observa que se preserva la norma \(2\) o Euclidiana del vector, las matrices de rotación Givens son matrices ortogonales y por tanto isometrías: \(||R_0v||_2=||v||_2\).

En el ejemplo anterior se hizo cero la entrada \(v_1\) de \(v\). Las matrices de rotación se utilizan para hacer ceros en entradas de un vector. Por ejemplo si \(v=(v_1,v_2)^T\) y se desea hacer cero la entrada \(v_2\) de \(v\) se puede utilizar la matriz de rotación:

\[\begin{split}R_O = \left[ \begin{array}{cc} \frac{v_1}{\sqrt{v_1^2+v_2^2}} & \frac{v_2}{\sqrt{v_1^2+v_2^2}}\\ -\frac{v_2}{\sqrt{v_1^2+v_2^2}} & \frac{v_1}{\sqrt{v_1^2+v_2^2}} \end{array} \right ] \end{split}\]

pues:

\[\begin{split}\begin{array}{l} \left[ \begin{array}{cc} \frac{v_1}{\sqrt{v_1^2+v_2^2}} & \frac{v_2}{\sqrt{v_1^2+v_2^2}}\\ -\frac{v_2}{\sqrt{v_1^2+v_2^2}} & \frac{v_1}{\sqrt{v_1^2+v_2^2}} \end{array} \right ] \cdot \left[\begin{array}{c} v_1\\ v_2 \end{array} \right]= \left[ \begin{array}{c} \frac{v_1^2+v_2^2}{\sqrt{v_1^2+v_2^2}}\\ \frac{-v_1v_2+v_1v_2}{\sqrt{v_1^2+v_2^2}} \end{array} \right ] = \left[ \begin{array}{c} \frac{v_1^2+v_2^2}{\sqrt{v_1^2+v_2^2}}\\ 0 \end{array} \right ]= \left[ \begin{array}{c} ||v||_2\\ 0 \end{array} \right ] \end{array} \end{split}\]

Y definiendo \(cos(\theta)=\frac{v_1}{\sqrt{v_1^2+v_2^2}}, sen(\theta)=\frac{v_2}{\sqrt{v_1^2+v_2^2}}\) se tiene :

\[\begin{split} R_O=\left[ \begin{array}{cc} cos\theta & sen\theta\\ -sen\theta & cos\theta \end{array} \right] \end{split}\]

que en el ejemplo anterior como \(v=(1,1)^T\) entonces: \(cos(\theta)=\frac{1}{\sqrt{2}}, sen(\theta)=\frac{1}{\sqrt{2}}\) por lo que \(\theta=\frac{\pi}{4}\) y:

\[\begin{split} R_O=\left[ \begin{array}{cc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right] \end{split}\]

que es una matriz de rotación para un ángulo que gira en sentido de las manecillas del reloj.

Para hacer cero la entrada \(v_1\) de \(v\) hay que usar:

\[\begin{split}\begin{array}{l} R_O=\left[ \begin{array}{cc} cos\theta & -sen\theta\\ sen\theta & cos\theta \end{array} \right] =\left[ \begin{array}{cc} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right] \end{array} \end{split}\]

que es una matriz de rotación para un ángulo que gira en sentido contrario de las manecillas del reloj.

Ejercicio

Utilizando lenguajes de programación usar una matriz de rotación Givens para rotar al vector \(v = (-3, 4)^T\) un ángulo de \(\frac{\pi}{3}\) en sentido de las manecillas del reloj. Graficar \(v\) y el vector rotado.

Ejemplo aplicando rotaciones Givens a una matriz

Las rotaciones Givens permiten hacer ceros en entradas de una matriz que son seleccionadas. Por ejemplo si se desea hacer cero la entrada \(x_4\) de \(x \in \mathbb{R}^4\), se definen \(cos\theta = \frac{x_2}{\sqrt{x_2^2 + x_4^2}}, sen\theta = \frac{x_4}{\sqrt{x_2^2 + x_4^2}}\) y

\[\begin{split} R_{24}^\theta= \left [ \begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & cos\theta & 0 & sen\theta \\ 0 & 0 & 1 & 0 \\ 0 & -sen\theta & 0 & cos\theta \end{array} \right ] \end{split}\]

entonces:

\[\begin{split} R_{24}^\theta x = \begin{array}{l} \left [ \begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & cos\theta & 0 & sen\theta \\ 0 & 0 & 1 & 0 \\ 0 & -sen\theta & 0 & cos\theta \end{array} \right ] \left [ \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array} \right ] = \left [ \begin{array}{c} x_1 \\ \sqrt{x_2^2 + x_4^2} \\ x_3 \\ 0 \end{array} \right ] \end{array} \end{split}\]

Y se escribe que se hizo una rotación en el plano \((2,4)\).

Observación

Obsérvese que sólo se modificaron dos entradas de \(x\): \(x_2, x_4\) por lo que el mismo efecto se obtiene al hacer la multiplicación:

\[\begin{split} \begin{array}{l} \left[ \begin{array}{cc} cos\theta & -sen\theta\\ sen\theta & cos\theta \end{array} \right] \left [ \begin{array}{c} x_2\\ x_4 \end{array} \right ] \end{array} \end{split}\]

para tales entradas.

Considérese a la matriz \(A \in \mathbb{R}^{4 \times 4}\):

\[\begin{split}A = \left [ \begin{array}{cccc} 4 & 1 & -2 & 2 \\ 1 & 2 & 0 & 1\\ -2 & 0 & 3 & -2 \\ 2 & 1 & -2 & -1 \end{array} \right ] \end{split}\]

y aplíquense rotaciones Givens para hacer ceros en las entradas debajo de la diagonal de \(A\) y tener una matriz triangular superior.

A = np.array([[4, 1, -2, 2],
              [1, 2, 0, 1],
              [-2, 0, 3, -2],
              [2, 1, -2, -1]], dtype=float)

Entrada \(a_{21}\), plano \((1,2)\):

idx_1 = 0
idx_2 = 1
idx_column = 0

print(A)

[[ 4.  1. -2.  2.]
 [ 1.  2.  0.  1.]
 [-2.  0.  3. -2.]
 [ 2.  1. -2. -1.]]

a_11 = A[idx_1,idx_column]
a_21 = A[idx_2,idx_column]
norm = math.sqrt(a_11**2 + a_21**2)
cos_theta = a_11/norm
sen_theta = a_21/norm

R12 = np.array([[cos_theta, sen_theta],
                [-sen_theta, cos_theta]])

print(R12)

[[ 0.97   0.243]
 [-0.243  0.97 ]]

Extraemos sólo los renglones a los que se les aplicará la matriz de rotación.

A_subset = np.row_stack((A[idx_1,:], A[idx_2,:]))

print(A_subset)

[[ 4.  1. -2.  2.]
 [ 1.  2.  0.  1.]]

print(R12@A_subset)

[[ 4.123  1.455 -1.94   2.183]
 [ 0.     1.698  0.485  0.485]]

A1_aux = R12@A_subset

print(A1_aux)

[[ 4.123  1.455 -1.94   2.183]
 [ 0.     1.698  0.485  0.485]]

Hacemos copia para un fácil manejo de los índices y matrices modificadas. Podríamos también usar numpy.view.

A1 = A.copy()

A1[idx_1, :] = A1_aux[0, :]
A1[idx_2, :] = A1_aux[1, :]

\(A^{(1)} = R_{12}^\theta A^{(0)}\).

print(A1)

[[ 4.123  1.455 -1.94   2.183]
 [ 0.     1.698  0.485  0.485]
 [-2.     0.     3.    -2.   ]
 [ 2.     1.    -2.    -1.   ]]

print(A)

[[ 4.  1. -2.  2.]
 [ 1.  2.  0.  1.]
 [-2.  0.  3. -2.]
 [ 2.  1. -2. -1.]]

Se preserva la norma 2 o Euclidiana de \(A[1:4,1]\).

print(np.linalg.norm(A1[:, idx_column]))

5.0

print(np.linalg.norm(A[:, idx_column]))

5.0

Entrada \(a_{31}\), plano \((1,3)\):

idx_1 = 0
idx_2 = 2
idx_column = 0

a_11 = A1[idx_1, idx_column]
a_31 = A1[idx_2, idx_column]
norm = math.sqrt(a_11**2 + a_31**2)
cos_theta = a_11/norm
sen_theta = a_31/norm

R13 = np.array([[cos_theta, sen_theta],
                [-sen_theta, cos_theta]])

print(R13)

[[ 0.9   -0.436]
 [ 0.436  0.9  ]]

Extraemos sólo los renglones a los que se les aplicará la matriz de rotación.

A1_subset = np.row_stack((A1[idx_1,:], A1[idx_2,:]))

print(A1_subset)

[[ 4.123  1.455 -1.94   2.183]
 [-2.     0.     3.    -2.   ]]

print(R13@A1_subset)

[[ 4.583  1.309 -3.055  2.837]
 [ 0.     0.635  1.852 -0.847]]

A2_aux = R13@A1_subset

print(A2_aux)

[[ 4.583  1.309 -3.055  2.837]
 [ 0.     0.635  1.852 -0.847]]

A2 = A1.copy()

A2[idx_1, :] = A2_aux[0, :]
A2[idx_2, :] = A2_aux[1, :]

\(A^{(2)} = R_{13}^\theta A^{(1)}\).

print(A2)

[[ 4.583  1.309 -3.055  2.837]
 [ 0.     1.698  0.485  0.485]
 [ 0.     0.635  1.852 -0.847]
 [ 2.     1.    -2.    -1.   ]]

print(A1)

[[ 4.123  1.455 -1.94   2.183]
 [ 0.     1.698  0.485  0.485]
 [-2.     0.     3.    -2.   ]
 [ 2.     1.    -2.    -1.   ]]

print(A)

[[ 4.  1. -2.  2.]
 [ 1.  2.  0.  1.]
 [-2.  0.  3. -2.]
 [ 2.  1. -2. -1.]]

Se preserva la norma 2 o Euclidiana de \(A[1:4,1]\).

print(np.linalg.norm(A2[:, idx_column]))

5.0

print(np.linalg.norm(A[:, idx_column]))

5.0

Entrada \(a_{41}\), plano \((1,4)\):

idx_1 = 0
idx_2 = 3
idx_column = 0

a_11 = A2[idx_1, idx_column]
a_41 = A2[idx_2, idx_column]
norm = math.sqrt(a_11**2 + a_41**2)
cos_theta = a_11/norm
sen_theta = a_41/norm

R14 = np.array([[cos_theta, sen_theta],
                [-sen_theta, cos_theta]])

print(R14)

[[ 0.917  0.4  ]
 [-0.4    0.917]]

Extraemos sólo los renglones a los que se les aplicará la matriz de rotación.

A2_subset = np.row_stack((A2[idx_1,:], A2[idx_2,:]))

print(A2_subset)

[[ 4.583  1.309 -3.055  2.837]
 [ 2.     1.    -2.    -1.   ]]

print(R14@A2_subset)

[[ 5.     1.6   -3.6    2.2  ]
 [ 0.     0.393 -0.611 -2.051]]

A3_aux = R14@A2_subset

print(A3_aux)

[[ 5.     1.6   -3.6    2.2  ]
 [ 0.     0.393 -0.611 -2.051]]

A3 = A2.copy()

A3[idx_1, :] = A3_aux[0, :]
A3[idx_2, :] = A3_aux[1, :]

\(A^{(3)} = R_{14}^\theta A^{(2)}\).

print(A3)

[[ 5.     1.6   -3.6    2.2  ]
 [ 0.     1.698  0.485  0.485]
 [ 0.     0.635  1.852 -0.847]
 [ 0.     0.393 -0.611 -2.051]]

print(A2)

[[ 4.583  1.309 -3.055  2.837]
 [ 0.     1.698  0.485  0.485]
 [ 0.     0.635  1.852 -0.847]
 [ 2.     1.    -2.    -1.   ]]

Se preserva la norma 2 o Euclidiana de \(A[1:4,1]\).

print(np.linalg.norm(A3[:, idx_column]))

5.0

print(np.linalg.norm(A[:, idx_column]))

5.0

Entrada \(a_{32}\), plano \((2,3)\):

idx_1 = 1
idx_2 = 2
idx_column = 1

a_22 = A3[idx_1, idx_column]
a_32 = A3[idx_2, idx_column]
norm = math.sqrt(a_22**2 + a_32**2)
cos_theta = a_22/norm
sen_theta = a_32/norm

R23 = np.array([[cos_theta, sen_theta],
                [-sen_theta, cos_theta]])

print(R23)

[[ 0.937  0.35 ]
 [-0.35   0.937]]

Extraemos sólo los renglones a los que se les aplicará la matriz de rotación.

A3_subset = np.row_stack((A3[idx_1,:], A3[idx_2,:]))

print(A3_subset)

[[ 0.     1.698  0.485  0.485]
 [ 0.     0.635  1.852 -0.847]]

print(R23@A3_subset)

[[ 0.     1.813  1.103  0.158]
 [ 0.     0.     1.565 -0.963]]

A4_aux = R23@A3_subset

print(A4_aux)

[[ 0.     1.813  1.103  0.158]
 [ 0.     0.     1.565 -0.963]]

A4 = A3.copy()

A4[idx_1, :] = A4_aux[0, :]
A4[idx_2, :] = A4_aux[1, :]

\(A^{(4)} = R_{23}^\theta A^{(3)}\).

print(A4)

[[ 5.     1.6   -3.6    2.2  ]
 [ 0.     1.813  1.103  0.158]
 [ 0.     0.     1.565 -0.963]
 [ 0.     0.393 -0.611 -2.051]]

print(A3)

[[ 5.     1.6   -3.6    2.2  ]
 [ 0.     1.698  0.485  0.485]
 [ 0.     0.635  1.852 -0.847]
 [ 0.     0.393 -0.611 -2.051]]

print(A2)

[[ 4.583  1.309 -3.055  2.837]
 [ 0.     1.698  0.485  0.485]
 [ 0.     0.635  1.852 -0.847]
 [ 2.     1.    -2.    -1.   ]]

Se preserva la norma 2 o Euclidiana de \(A[1:4,2]\).

print(np.linalg.norm(A4[:, idx_column]))

2.449489742783178

print(np.linalg.norm(A[:, idx_column]))

2.449489742783178

Ejercicio

Utilizando lenguajes de programación finalizar el ejercicio para llevar a la matriz \(A\) a una matriz triangular superior.

Cálculo del factor \(Q\) en la factorización \(QR\) con rotaciones Givens

El ejemplo anterior mostró que si \(R_i \in \mathbb{R}^{m \times m}\) es rotación Givens y \(A \in \mathbb{R}^{m \times n}\) entonces:

\[R = R_nR_{n-1} \cdots R_1A\]

con \(R \in \mathbb{R}^{m \times n}\) una matriz triangular superior. Por lo tanto:

\[Q^T = R_nR_{n-1} \cdots R_1\]

y

\[A = QR.\]

Ejercicios

1.Resuelve los ejercicios y preguntas de la nota.

Preguntas de comprehensión.

1)Escribe ejemplos de operaciones vectoriales y matriciales básicas del Álgebra Lineal Numérica.

2)¿Para qué se utilizan las transformaciones de Gauss?

3)Escribe nombres de factorizaciones en las que se utilizan las transformaciones de Gauss.

4)Escribe propiedades que tiene una matriz ortogonal.

5)¿Una matriz ortogonal es rectangular?

6)¿Qué propiedades tienen las matrices de proyección, reflexión y rotación?

7)¿Qué problema numérico se quiere resolver al definir un vector de Householder como \(x+signo(x_1)||x||_2e_1\)?

Referencias:

1. G. H. Golub, C. F. Van Loan, Matrix Computations, John Hopkins University Press, 2013.