5.3 Compilación a C

Notas para contenedor de docker:

Comando de docker para ejecución de la nota de forma local:

nota: cambiar <ruta a mi directorio> por la ruta de directorio que se desea mapear a /datos dentro del contenedor de docker y <versión imagen de docker> por la versión más actualizada que se presenta en la documentación.

docker run --rm -v <ruta a mi directorio>:/datos --name jupyterlab_optimizacion_2 -p 8888:8888 -d palmoreck/jupyterlab_optimizacion_2:<versión imagen de docker>

password para jupyterlab: qwerty

Detener el contenedor de docker:

docker stop jupyterlab_optimizacion_2

Documentación de la imagen de docker palmoreck/jupyterlab_optimizacion_2:<versión imagen de docker> en liga.

---

Al final de esta nota la comunidad lectora:

• Comprenderá diferencias entre lenguajes de programación que son intérpretes y los que requieren/realizan pasos de compilación.

• Comprenderá por qué definir tipo de valores en lenguajes que son intérpretes conducen a tiempos de ejecución menores.

• Aprenderá lo que es una compilación ahead of time (AOT) y just in time (JIT). Se mostrarán ejemplos de lenguajes y paquetes que realizan ambos tipos de compilaciones.

Se presentan códigos y sus ejecuciones en una máquina m4.16xlarge con una AMI ubuntu 20.04 - ami-042e8287309f5df03 de la nube de AWS. Se utilizó en la sección de User data el script_profiling_and_BLAS.sh

La máquina m4.16xlarge tiene las siguientes características:

%%bash
lscpu

Architecture:                    x86_64
CPU op-mode(s):                  32-bit, 64-bit
Byte Order:                      Little Endian
Address sizes:                   46 bits physical, 48 bits virtual
CPU(s):                          64
On-line CPU(s) list:             0-63
Thread(s) per core:              2
Core(s) per socket:              16
Socket(s):                       2
NUMA node(s):                    2
Vendor ID:                       GenuineIntel
CPU family:                      6
Model:                           79
Model name:                      Intel(R) Xeon(R) CPU E5-2686 v4 @ 2.30GHz
Stepping:                        1
CPU MHz:                         3000.000
CPU max MHz:                     3000.0000
CPU min MHz:                     1200.0000
BogoMIPS:                        4600.00
Hypervisor vendor:               Xen
Virtualization type:             full
L1d cache:                       1 MiB
L1i cache:                       1 MiB
L2 cache:                        8 MiB
L3 cache:                        90 MiB
NUMA node0 CPU(s):               0-15,32-47
NUMA node1 CPU(s):               16-31,48-63
Vulnerability Itlb multihit:     KVM: Mitigation: VMX unsupported
Vulnerability L1tf:              Mitigation; PTE Inversion
Vulnerability Mds:               Vulnerable: Clear CPU buffers attempted, no microcode; SMT Host state unknown
Vulnerability Meltdown:          Mitigation; PTI
Vulnerability Spec store bypass: Vulnerable
Vulnerability Spectre v1:        Mitigation; usercopy/swapgs barriers and __user pointer sanitization
Vulnerability Spectre v2:        Mitigation; Full generic retpoline, STIBP disabled, RSB filling
Vulnerability Srbds:             Not affected
Vulnerability Tsx async abort:   Vulnerable: Clear CPU buffers attempted, no microcode; SMT Host state unknown
Flags:                           fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse36 clflush mmx fxsr sse sse2 ht syscall nx pdpe1gb rdtscp lm constant_tsc arch_perfmon rep_good nopl xtopology nonstop_tsc cpuid aperfmperf tsc_known_freq pni pclmulqdq monitor est ssse3 fma cx16 pcid sse4_1 sse4_2 x2apic movbe popcnt tsc_deadline_timer aes xsave avx f16c rdrand hypervisor lahf_lm abm cpuid_fault invpcid_single pti fsgsbase bmi1 hle avx2 smep bmi2 erms invpcid rtm xsaveopt ida

%%bash
sudo lshw -C memory

  *-firmware
       description: BIOS
       vendor: Xen
       physical id: 0
       version: 4.11.amazon
       date: 08/24/2006
       size: 96KiB
       capabilities: pci edd
  *-memory
       description: System Memory
       physical id: 1000
       size: 256GiB
       capabilities: ecc
       configuration: errordetection=multi-bit-ecc
     *-bank:0
          description: DIMM RAM
          physical id: 0
          slot: DIMM 0
          size: 16GiB
          width: 64 bits
     *-bank:1
          description: DIMM RAM
          physical id: 1
          slot: DIMM 1
          size: 16GiB
          width: 64 bits
     *-bank:2
          description: DIMM RAM
          physical id: 2
          slot: DIMM 2
          size: 16GiB
          width: 64 bits
     *-bank:3
          description: DIMM RAM
          physical id: 3
          slot: DIMM 3
          size: 16GiB
          width: 64 bits
     *-bank:4
          description: DIMM RAM
          physical id: 4
          slot: DIMM 4
          size: 16GiB
          width: 64 bits
     *-bank:5
          description: DIMM RAM
          physical id: 5
          slot: DIMM 5
          size: 16GiB
          width: 64 bits
     *-bank:6
          description: DIMM RAM
          physical id: 6
          slot: DIMM 6
          size: 16GiB
          width: 64 bits
     *-bank:7
          description: DIMM RAM
          physical id: 7
          slot: DIMM 7
          size: 16GiB
          width: 64 bits
     *-bank:8
          description: DIMM RAM
          physical id: 8
          slot: DIMM 8
          size: 16GiB
          width: 64 bits
     *-bank:9
          description: DIMM RAM
          physical id: 9
          slot: DIMM 9
          size: 16GiB
          width: 64 bits
     *-bank:10
          description: DIMM RAM
          physical id: a
          slot: DIMM 10
          size: 16GiB
          width: 64 bits
     *-bank:11
          description: DIMM RAM
          physical id: b
          slot: DIMM 11
          size: 16GiB
          width: 64 bits
     *-bank:12
          description: DIMM RAM
          physical id: c
          slot: DIMM 12
          size: 16GiB
          width: 64 bits
     *-bank:13
          description: DIMM RAM
          physical id: d
          slot: DIMM 13
          size: 16GiB
          width: 64 bits
     *-bank:14
          description: DIMM RAM
          physical id: e
          slot: DIMM 14
          size: 16GiB
          width: 64 bits
     *-bank:15
          description: DIMM RAM
          physical id: f
          slot: DIMM 15
          size: 16GiB
          width: 64 bits

%%bash
uname -ar #r for kernel, a for all

Linux ip-10-0-2-123 5.11.0-1022-aws #23~20.04.1-Ubuntu SMP Mon Nov 15 14:03:19 UTC 2021 x86_64 x86_64 x86_64 GNU/Linux

Observación

En la celda anterior se utilizó el comando de magic %%bash. Algunos comandos de magic los podemos utilizar también con import. Ver ipython-magics

Características de los lenguajes de programación

Los lenguajes de programación y sus implementaciones tienen características como las siguientes:

• Realizar un parsing de las instrucciones y ejecutarlas de forma casi inmediata (intérprete). Como ejemplo está el lenguaje: Beginners’ All-purpose Symbolic Instruction Code: BASIC

• Realizar un parsing de las instrucciones, traducirlas a una representación intermedia (IR) y ejecutarlas. La traducción a una representación intermedia es un bytecode. Como ejemplo se encuentra el lenguaje Python en su implementación CPython.

• Compilar ahead of time (AOT) las instrucciones antes de su ejecución. Como ejemplo se encuentran los lenguajes C, C++ y Fortran.

• Realizar un parsing de las instrucciones y compilarlas en una forma just in time compilation (JIT) at runtime. Como ejemplos se encuentran los lenguajes Julia y Python en su implementación con PyPy.

La ejecución de instrucciones será más rápida dependiendo del lenguaje, la implementación que se haga del mismo y de sus features.

Comentarios

• Varios proyectos están en desarrollo para mejorar eficiencia y otros temas. Algunos de ellos son:

  • PyPy

  • A better API for extending Python in C: hpyproject

• La implementación CPython de Python es la estándar, pero hay otras más como PyPy. Ver python-vs-cpython para una breve explicación de implementaciones de Python. Ver Alternative R implementations y R implementations para implementaciones de R diferentes a la estándar.

Cpython

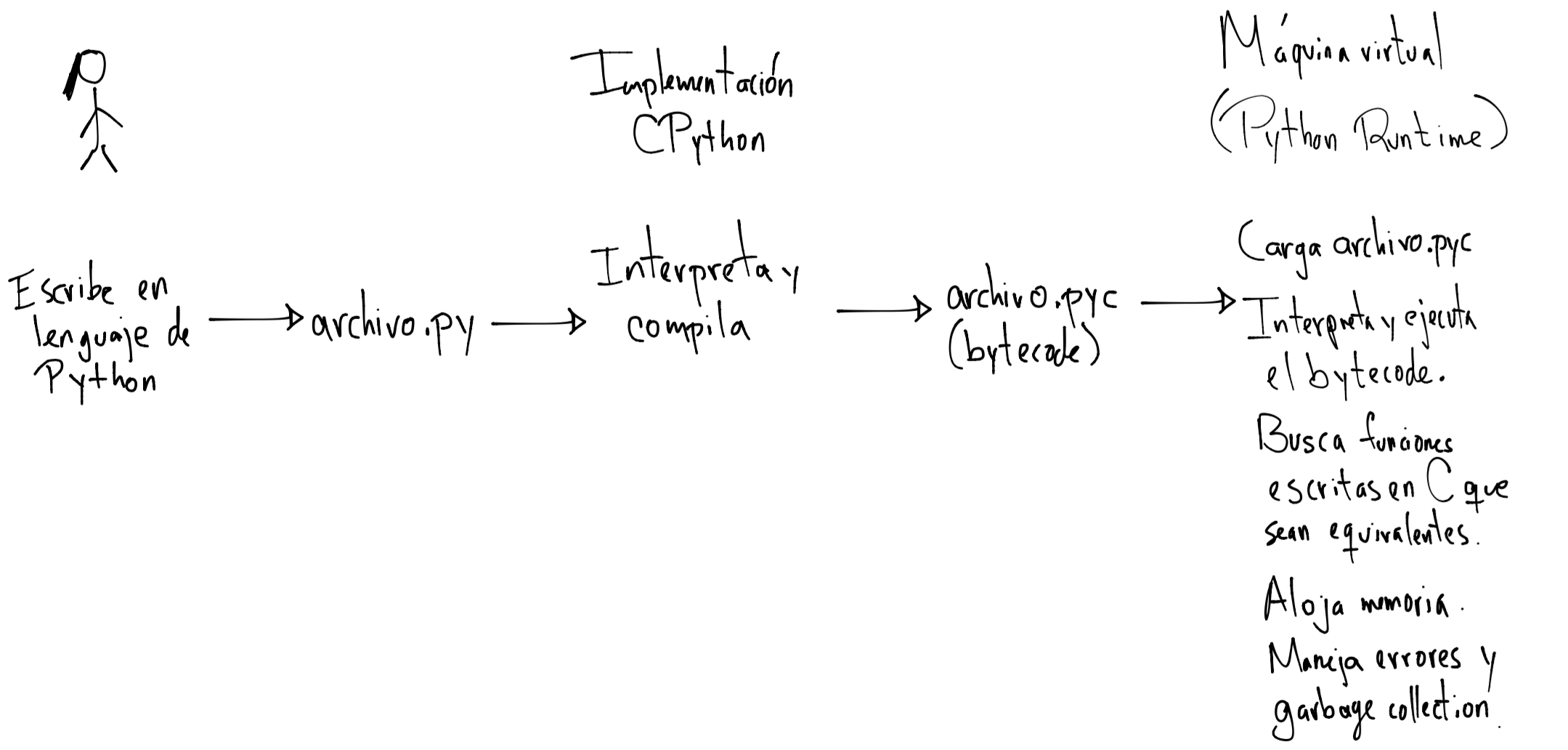
Compilación AOT y JIT

Es común utilizar la palabra librería en lugar de paquete en el contexto de compilación.

Una compilación AOT crea una librería, especializada para nuestras máquinas y se puede utilizar de forma instantánea. Un ejemplo de lo anterior lo tenemos con Cython, el cual es un paquete que realiza la compilación de módulos de Python. Por ejemplo, las librerías de NumPy, SciPy o Scikit-learn instalados vía pip o conda utilizan Cython para compilar secciones de tales librerías adaptadas a nuestras máquinas.

Una compilación JIT no requiere que se realice “trabajo previo” de nuestro lado, la compilación se realiza al tiempo que se utiliza el código, at runtime. En términos coloquiales, en una compilación JIT, se iniciará la ejecución del código identificando diferentes secciones que pueden compilarse y que por tanto se ejecutarán más lentamente de lo normal pues se estará realizando la compilación al tiempo de ejecución. Sin embargo, en sucesivas ejecuciones del mismo código tales secciones serán más rápidas. En resúmen se requiere un warm-up, ver por ejemplo how-fast-is-pypy.

La compilación AOT da los mejores speedups pero solicita mayor trabajo de nuestro lado. La compilación JIT da buenos speedups con poca intervención nuestra pero utiliza más memoria y más tiempo en iniciar la ejecución del código, ver por ejemplo python_performance-slide-15 acerca de PyPy issues.

Para la ejecución frecuente de scripts pequeños la compilación AOT resulta una mejor opción que la compilación JIT, ver por ejemplo couldn’t the jit dump and reload already compiled machine code.

A continuación se presentan ejecuciones en diferentes lenguajes con sus implementaciones estándar para aproximar el área debajo de la curva de \(f(x) = e^{-x^2}\) en el intervalo \([0, 1]\) con la regla del rectángulo compuesto. Se mide el tiempo de ejecución utilizando \(n = 10^7\) nodos.

Python

%%file Rcf_python.py
import math
import time
def Rcf(f,a,b,n):
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
    
        f (float): function expression of integrand.
        
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    h_hat = (b-a)/n
    sum_res = 0
    for i in range(n):
        x = a+(i+1/2)*h_hat
        sum_res += f(x)
    return h_hat*sum_res

if __name__ == "__main__":   
    n = 10**7
    f = lambda x: math.exp(-x**2)
    a = 0
    b = 1
    start_time = time.time()
    res = Rcf(f,a,b,n)
    end_time = time.time()
    secs = end_time-start_time
    print("Rcf tomó", secs, "segundos" )

Writing Rcf_python.py

%%bash
python3 Rcf_python.py

Rcf tomó 3.4967801570892334 segundos

R

%%file Rcf_R.R
Rcf<-function(f,a,b,n){
    '
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
    
        f (float): function expression of integrand.
        
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    '
    
    h_hat <- (b-a)/n
    sum_res <- 0
    for(i in 0:(n-1)){
        x <- a+(i+1/2)*h_hat
        sum_res <- sum_res + f(x)
    }
    approx <- h_hat*sum_res
}
n <- 10**7
f <- function(x)exp(-x^2)
a <- 0
b <- 1
system.time(Rcf(f,a,b,n))

Writing Rcf_R.R

%%bash
Rscript Rcf_R.R

   user  system elapsed 
  5.607   0.018   5.626 

Julia

Ver: Julia: performance-tips

%%file Rcf_julia.jl
"""
Compute numerical approximation using rectangle or mid-point
method in an interval.

# Arguments

- `f::Float`: function expression of integrand.
- `a::Float`: left point of interval.
- `b::Float`: right point of interval.
- `n::Integer`: number of subintervals.
"""
function Rcf(f, a, b, n)
    h_hat = (b-a)/n
    sum_res = 0
    for i in 0.0:n-1
        x = a+(i+1/2)*h_hat
        sum_res += f(x)
    end    
    return h_hat*sum_res
end
function main()
    a = 0
    b = 1
    n =10^7
    f(x) = exp(-x^2)
    res(f, a, b, n) = @time Rcf(f, a, b, n)
    println(res(f, a, b, n))
    println(res(f, a, b, n))
end

main()

Writing Rcf_julia.jl

%%bash
/usr/local/julia-1.7.1/bin/julia Rcf_julia.jl

  0.239888 seconds (2.63 k allocations: 142.609 KiB, 41.51% compilation time)
0.7468241328123898
  0.140050 seconds (2 allocations: 32 bytes)
0.7468241328123898

Rcf_julia_typed_values.jl

%%file Rcf_julia_typed_values.jl
"""
Compute numerical approximation using rectangle or mid-point
method in an interval.

# Arguments

- `f::Float`: function expression of integrand.
- `a::Float`: left point of interval.
- `b::Float`: right point of interval.
- `n::Integer`: number of subintervals.
"""
function Rcf(f, a, b, n)
    h_hat = (b-a)/n
    sum_res = 0.0
    for i in 0:n-1
        x = a+(i + 1/2)*h_hat
        sum_res += f(x)
    end    
    return h_hat*sum_res
end
function main()
    a = 0.0
    b = 1.0
    n =10^7
    f(x) = exp(-x^2)
    res(f, a, b, n) = @time Rcf(f, a, b, n)
    println(res(f, a, b, n))
    println(res(f, a, b, n))
end

main()

Writing Rcf_julia_typed_values.jl

%%bash
/usr/local/julia-1.7.1/bin/julia Rcf_julia_typed_values.jl

  0.143176 seconds (503 allocations: 26.594 KiB, 11.97% compilation time)
0.7468241328123898
  0.125599 seconds (4 allocations: 64 bytes)
0.7468241328123898

Rcf_julia_naive.jl

%%file Rcf_julia_naive.jl
"""
Compute numerical approximation using rectangle or mid-point
method in an interval.

# Arguments

- `f::Float`: function expression of integrand.
- `a::Float`: left point of interval.
- `b::Float`: right point of interval.
- `n::Integer`: number of subintervals.
"""
function Rcf(f, a, b, n)
    h_hat = (b-a)/n
    sum_res = 0
    for i in 0:n-1
        x = a+(i + 1/2)*h_hat
        sum_res += f(x)
    end    
    return h_hat*sum_res
end
function main()
    a = 0
    b = 1
    n =10^7
    f(x) = exp(-x^2)
    res(f, a, b, n) = @time Rcf(f, a, b, n)
    println(res(f, a, b, n))
    println(res(f, a, b, n))
end

main()

Writing Rcf_julia_naive.jl

%%bash
/usr/local/julia-1.7.1/bin/julia Rcf_julia_naive.jl

  0.113146 seconds (588 allocations: 31.391 KiB, 17.07% compilation time)
0.7468241328123898
  0.094084 seconds (2 allocations: 32 bytes)
0.7468241328123898

C

Para la medición de tiempos se utilizaron las ligas: measuring-time-in-millisecond-precision y find-execution-time-c-program.

Rcf_c.c

%%file Rcf_c.c
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
#include <sys/time.h>

void Rcf(double ext_izq, double ext_der, int n,\
    double *sum_res_p);
double f(double nodo);

int main(int argc, char *argv[]){
    double sum_res = 0.0;
    double a = 0.0, b = 1.0;
    int n = 1e7;
    struct timeval start;
    struct timeval end;
    long seconds;
    long long mili;
    
    gettimeofday(&start, NULL);
    Rcf(a,b,n,&sum_res);
    gettimeofday(&end, NULL);
    seconds = (end.tv_sec - start.tv_sec);
    mili = 1000*(seconds) + (end.tv_usec - start.tv_usec)/1000;    
    printf("Tiempo de ejecución: %lld milisegundos", mili);
    
    return 0;
}
void Rcf(double a, double b, int n, double *sum){
    double h_hat = (b-a)/n;
    double x = 0.0;
    int i = 0;
    *sum = 0.0;
    for(i = 0; i <= n-1; i++){
        x = a+(i+1/2.0)*h_hat;
        *sum += f(x);
    }
    *sum = h_hat*(*sum);
}
double f(double nodo){
    double valor_f;
    valor_f = exp(-pow(nodo,2));
    return valor_f;
}

Writing Rcf_c.c

%%bash
gcc -Wall Rcf_c.c -o Rcf_c.out -lm

%%bash
./Rcf_c.out

Tiempo de ejecución: 478 milisegundos

¿Por qué dar información sobre el tipo de valores (u objetos) que se utilizan en un código ayuda a que su ejecución sea más rápida?

Python es dynamically typed que se refiere a que un objeto de cualquier tipo y cualquier statement que haga referencia a un objeto, pueden cambiar su tipo. Esto hace difícil que la máquina virtual pueda optimizar la ejecución del código pues no se conoce qué tipo será utilizado para las operaciones futuras. Por ejemplo:

v = -1.0

print(type(v), abs(v))

<class 'float'> 1.0

v = 1 - 1j

print(type(v), abs(v))

<class 'complex'> 1.4142135623730951

La función abs trabaja diferente dependiendo del tipo de objeto. Para un número entero o punto flotante regresa el negativo de \(-1.0\) y para un número complejo calcula una norma Euclidiana tomando de \(v\) su parte real e imaginaria: \(\text{abs}(v) = \sqrt{v.real^2 + v.imag^2}\).

Lo anterior en la práctica implica la ejecución de más instrucciones y por tanto mayor tiempo en ejecutarse. Antes de llamar a abs en la variable, Python revisa el tipo y decide cuál método llamar (overhead).

Comentarios

• Además cada número en Python está wrapped up en un objeto de Python de alto nivel. Por ejemplo para un entero se tiene el objeto int. Tal objeto tiene otras funciones por ejemplo __str__ para imprimirlo.

• Es muy común que en los códigos no cambien los tipos por lo que la compilación AOT es una buena opción para una ejecución más rápida.

• Siguiendo con los dos comentarios anteriores, si sólo se desea calcular operaciones matemáticas (como el caso de la raíz cuadrada anterior) no requerimos la funcionalidad del objeto de alto nivel.

Cython

• Es un compilador que traduce instrucciones anotadas y escritas en un lenguaje híbrido entre Python y C que resultan un módulo compilado. Este módulo puede ser importado como un módulo regular de Python utilizando import. Típicamente el módulo compilado resulta ser similar en sintaxis al lenguaje C.

La frase código tipo CPU-bound es código cuya ejecución involucra un porcentaje mayor para uso de CPU que uso de memoria o I/O.

• Tiene un buen tiempo en la comunidad (2007 aproximadamente), es altamente usado y es de las herramientas preferidas para código tipo CPU-bound. Es un fork de Pyrex (2002) que expande sus capacidades.

Comentario

Pyrex en términos simples es Python con manejo de tipo de valores de C. Pyrex traduce el código escrito en Python a código de C (lo cual evita el uso de la Python/C API) y permite la declaración de parámetros o valores en tipos de valores de C.

• Requiere conocimiento del lenguaje C lo cual debe tomarse en cuenta en un equipo de desarrollo de software y se sugiere utilizarlo en secciones pequeñas del código.

• Soporta la API OpenMP para aprovechar los múltiples cores de una máquina.

• Puede utilizarse vía un script setup.py que compila un módulo para usarse con import y también puede utilizarse en IPython vía un comando magic.

Comentario

En el paso de compilación a código de máquina del dibujo anterior se omitieron detalles como son: creación de un archivo .c y compilación de tal archivo con el compilador gcc al módulo compilado (en sistemas Unix tiene extensión .so).

Ver machine code

• Cython y el compilador gcc analizan el código anotado para determinar qué instrucciones pueden optimizarse mediante una compilación AOT.

¿En qué casos y qué tipo de ganancias en velocidad podemos esperar al usar Cython?

• Un caso es en el que se tenga un código con muchos loops que realicen operaciones matemáticas típicamente no vectorizadas o que no pueden vectorizarse. Esto es, códigos en los que las instrucciones son básicamente sólo Python sin utilizar paquetes externos. Además, si en el ciclo las variables no cambian de su tipo (por ejemplo de int a float) entonces es un código que obtendrá ganancia en velocidad al compilar a código de máquina.

Observación

Si tu código de Python llama a operaciones vectorizadas vía NumPy podría ser que no se ejecute más rápido tu código después de compilarlo. Principalmente porque probablemente no se crearán muchos objetos intermedios que es un feature de NumPy.

• No esperamos tener un speedup después de compilar para llamadas a librerías externas (por ejemplo paqueterías que manejan bases de datos). También es poco probable que se obtengan ganancias significativas en programas que tengan alta carga de I/O.

• En general es poco probable que tu código compilado se ejecute más rápido que un código en C “bien escrito” y también es poco probable que se ejecute más lento. Es muy posible que el código C generado desde Python mediante Cython pueda alcanzar las velocidades de un código escrito en C, a menos que la persona que programó en C tenga un gran conocimiento de formas de hacer que el código de C se ajuste a la arquitectura de la máquina sobre la que se ejecutan los códigos.

Ejemplo utilizando un archivo setup.py

import math
import time

from pytest import approx
from scipy.integrate import quad
from IPython.display import HTML, display

Para este caso requerimos tres archivos:

1.El código que será compilado en un archivo con extensión .pyx (escrito en Python).

Observación

La extensión .pyx se utiliza en el lenguaje Pyrex.

2.Un archivo setup.py que contiene las instrucciones para llamar a Cython y se encarga de crear el módulo compilado.

3.El código escrito en Python que importará el módulo compilado.

Archivo .pyx:

%%file Rcf_cython.pyx
def Rcf(f,a,b,n): #Rcf: rectángulo compuesto para f
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
    
        f (float): function expression of integrand.
        
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    h_hat = (b-a)/n
    nodes = [a+(i+1/2)*h_hat for i in range(n)]
    sum_res = 0
    for node in nodes:
        sum_res = sum_res+f(node)
    return h_hat*sum_res

Writing Rcf_cython.pyx

Archivo setup.py que contiene las instrucciones para el build:

%%file setup.py
from distutils.core import setup
from Cython.Build import cythonize

setup(ext_modules = cythonize("Rcf_cython.pyx", 
                              compiler_directives={'language_level' : 3})
     )

Writing setup.py

Compilar desde la línea de comandos:

%%bash
python3 setup.py build_ext --inplace

Compiling Rcf_cython.pyx because it changed.
[1/1] Cythonizing Rcf_cython.pyx
running build_ext
building 'Rcf_cython' extension
creating build
creating build/temp.linux-x86_64-3.8
x86_64-linux-gnu-gcc -pthread -Wno-unused-result -Wsign-compare -DNDEBUG -g -fwrapv -O2 -Wall -g -fstack-protector-strong -Wformat -Werror=format-security -g -fwrapv -O2 -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -I/usr/include/python3.8 -c Rcf_cython.c -o build/temp.linux-x86_64-3.8/Rcf_cython.o
x86_64-linux-gnu-gcc -pthread -shared -Wl,-O1 -Wl,-Bsymbolic-functions -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fwrapv -O2 -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fwrapv -O2 -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 build/temp.linux-x86_64-3.8/Rcf_cython.o -o /home/ubuntu/analisis-numerico-computo-cientifico/libro_optimizacion/temas/V.optimizacion_de_codigo/5.3/Rcf_cython.cpython-38-x86_64-linux-gnu.so

Importar módulo compilado y ejecutarlo:

f=lambda x: math.exp(-x**2) #using math library

n = 10**7
a = 0
b = 1

import Rcf_cython

start_time = time.time()
res = Rcf_cython.Rcf(f, a, b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf tomó",secs,"segundos" )

Rcf tomó 3.731260061264038 segundos

obj, err = quad(f, a, b)

print(res == approx(obj))

True

Comando de magic %cython

Ver extensions-bundled-with-ipython para extensiones que antes se incluían en Ipython.

Al instalar Cython se incluye tal comando. Al ejecutarse crea el archivo .pyx, lo compila con setup.py e importa en el notebook.

%load_ext Cython

%%cython
def Rcf(f,a,b,n):
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
    
        f (float): function expression of integrand.
        
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    h_hat = (b-a)/n
    nodes = [a+(i+1/2)*h_hat for i in range(n)]
    sum_res = 0
    for node in nodes:
        sum_res = sum_res+f(node)
    return h_hat*sum_res

start_time = time.time()
res = Rcf(f, a, b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf tomó",secs,"segundos" )

Rcf tomó 3.7382779121398926 segundos

obj, err = quad(f, a, b)

print(res == approx(obj))

True

Anotaciones para analizar un bloque de código

Cython tiene la opción de annotation para generar un archivo con extensión .html en el que cada línea puede ser expandida haciendo un doble click que mostrará el código C generado. Líneas “más amarillas” refieren a más llamadas en la máquina virtual de Python, mientras que líneas más blancas significan “más código en C y no Python”.

El objetivo es remover la mayor cantidad de líneas amarillas posibles pues son costosas en tiempo. Si tales líneas están dentro de loops serán todavía más costosas. Al final se busca tener códigos cuyas anotaciones sean lo más blancas posibles.

Observación

Concentra tu atención en las líneas que son amarillas y están dentro de los loops, no inviertas tiempo en líneas amarillas que están fuera de loops y que no causan una ejecución lenta. Una ayuda para identificar lo anterior la da el perfilamiento.

Ejemplo vía línea de comando

%%bash
$HOME/.local/bin/cython --force -3 --annotate Rcf_cython.pyx

Ver archivo creado: Rcf_cython.html

La liga correcta del archivo Rcf_cython.c es Rcf_cython.c

display(HTML("Rcf_cython.html"))

Generated by Cython 0.29.22

Yellow lines hint at Python interaction.
Click on a line that starts with a "+" to see the C code that Cython generated for it.

Raw output: Rcf_cython.c

+01: def Rcf(f,a,b,n): #Rcf: rectángulo compuesto para f

/* Python wrapper */
static PyObject *__pyx_pw_10Rcf_cython_1Rcf(PyObject *__pyx_self, PyObject *__pyx_args, PyObject *__pyx_kwds); /*proto*/
static char __pyx_doc_10Rcf_cython_Rcf[] = "\n    Compute numerical approximation using rectangle or mid-point\n    method in an interval.\n    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for\n    i=0,1,...,n-1 and h_hat=(b-a)/n\n    Args:\n    \n        f (float): function expression of integrand.\n        \n        a (float): left point of interval.\n        \n        b (float): right point of interval.\n        \n        n (int): number of subintervals.\n        \n    Returns:\n    \n        sum_res (float): numerical approximation to integral\n            of f in the interval a,b\n    ";
static PyMethodDef __pyx_mdef_10Rcf_cython_1Rcf = {"Rcf", (PyCFunction)(void*)(PyCFunctionWithKeywords)__pyx_pw_10Rcf_cython_1Rcf, METH_VARARGS|METH_KEYWORDS, __pyx_doc_10Rcf_cython_Rcf};
static PyObject *__pyx_pw_10Rcf_cython_1Rcf(PyObject *__pyx_self, PyObject *__pyx_args, PyObject *__pyx_kwds) {
  PyObject *__pyx_v_f = 0;
  PyObject *__pyx_v_a = 0;
  PyObject *__pyx_v_b = 0;
  PyObject *__pyx_v_n = 0;
  PyObject *__pyx_r = 0;
  __Pyx_RefNannyDeclarations
  __Pyx_RefNannySetupContext("Rcf (wrapper)", 0);
  {
    static PyObject **__pyx_pyargnames[] = {&__pyx_n_s_f,&__pyx_n_s_a,&__pyx_n_s_b,&__pyx_n_s_n,0};
    PyObject* values[4] = {0,0,0,0};
    if (unlikely(__pyx_kwds)) {
      Py_ssize_t kw_args;
      const Py_ssize_t pos_args = PyTuple_GET_SIZE(__pyx_args);
      switch (pos_args) {
        case  4: values[3] = PyTuple_GET_ITEM(__pyx_args, 3);
        CYTHON_FALLTHROUGH;
        case  3: values[2] = PyTuple_GET_ITEM(__pyx_args, 2);
        CYTHON_FALLTHROUGH;
        case  2: values[1] = PyTuple_GET_ITEM(__pyx_args, 1);
        CYTHON_FALLTHROUGH;
        case  1: values[0] = PyTuple_GET_ITEM(__pyx_args, 0);
        CYTHON_FALLTHROUGH;
        case  0: break;
        default: goto __pyx_L5_argtuple_error;
      }
      kw_args = PyDict_Size(__pyx_kwds);
      switch (pos_args) {
        case  0:
        if (likely((values[0] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_f)) != 0)) kw_args--;
        else goto __pyx_L5_argtuple_error;
        CYTHON_FALLTHROUGH;
        case  1:
        if (likely((values[1] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_a)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 4, 4, 1); __PYX_ERR(0, 1, __pyx_L3_error)
        }
        CYTHON_FALLTHROUGH;
        case  2:
        if (likely((values[2] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_b)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 4, 4, 2); __PYX_ERR(0, 1, __pyx_L3_error)
        }
        CYTHON_FALLTHROUGH;
        case  3:
        if (likely((values[3] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_n)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 4, 4, 3); __PYX_ERR(0, 1, __pyx_L3_error)
        }
      }
      if (unlikely(kw_args > 0)) {
        if (unlikely(__Pyx_ParseOptionalKeywords(__pyx_kwds, __pyx_pyargnames, 0, values, pos_args, "Rcf") < 0)) __PYX_ERR(0, 1, __pyx_L3_error)
      }
    } else if (PyTuple_GET_SIZE(__pyx_args) != 4) {
      goto __pyx_L5_argtuple_error;
    } else {
      values[0] = PyTuple_GET_ITEM(__pyx_args, 0);
      values[1] = PyTuple_GET_ITEM(__pyx_args, 1);
      values[2] = PyTuple_GET_ITEM(__pyx_args, 2);
      values[3] = PyTuple_GET_ITEM(__pyx_args, 3);
    }
    __pyx_v_f = values[0];
    __pyx_v_a = values[1];
    __pyx_v_b = values[2];
    __pyx_v_n = values[3];
  }
  goto __pyx_L4_argument_unpacking_done;
  __pyx_L5_argtuple_error:;
  __Pyx_RaiseArgtupleInvalid("Rcf", 1, 4, 4, PyTuple_GET_SIZE(__pyx_args)); __PYX_ERR(0, 1, __pyx_L3_error)
  __pyx_L3_error:;
  __Pyx_AddTraceback("Rcf_cython.Rcf", __pyx_clineno, __pyx_lineno, __pyx_filename);
  __Pyx_RefNannyFinishContext();
  return NULL;
  __pyx_L4_argument_unpacking_done:;
  __pyx_r = __pyx_pf_10Rcf_cython_Rcf(__pyx_self, __pyx_v_f, __pyx_v_a, __pyx_v_b, __pyx_v_n);
  int __pyx_lineno = 0;
  const char *__pyx_filename = NULL;
  int __pyx_clineno = 0;

  /* function exit code */
  __Pyx_RefNannyFinishContext();
  return __pyx_r;
}

static PyObject *__pyx_pf_10Rcf_cython_Rcf(CYTHON_UNUSED PyObject *__pyx_self, PyObject *__pyx_v_f, PyObject *__pyx_v_a, PyObject *__pyx_v_b, PyObject *__pyx_v_n) {
  PyObject *__pyx_v_h_hat = NULL;
  PyObject *__pyx_v_nodes = NULL;
  PyObject *__pyx_v_sum_res = NULL;
  PyObject *__pyx_v_node = NULL;
  PyObject *__pyx_7genexpr__pyx_v_i = NULL;
  PyObject *__pyx_r = NULL;
  __Pyx_RefNannyDeclarations
  __Pyx_RefNannySetupContext("Rcf", 0);
/* … */
  /* function exit code */
  __pyx_L1_error:;
  __Pyx_XDECREF(__pyx_t_1);
  __Pyx_XDECREF(__pyx_t_2);
  __Pyx_XDECREF(__pyx_t_3);
  __Pyx_XDECREF(__pyx_t_6);
  __Pyx_AddTraceback("Rcf_cython.Rcf", __pyx_clineno, __pyx_lineno, __pyx_filename);
  __pyx_r = NULL;
  __pyx_L0:;
  __Pyx_XDECREF(__pyx_v_h_hat);
  __Pyx_XDECREF(__pyx_v_nodes);
  __Pyx_XDECREF(__pyx_v_sum_res);
  __Pyx_XDECREF(__pyx_v_node);
  __Pyx_XDECREF(__pyx_7genexpr__pyx_v_i);
  __Pyx_XGIVEREF(__pyx_r);
  __Pyx_RefNannyFinishContext();
  return __pyx_r;
}
/* … */
  __pyx_tuple_ = PyTuple_Pack(9, __pyx_n_s_f, __pyx_n_s_a, __pyx_n_s_b, __pyx_n_s_n, __pyx_n_s_h_hat, __pyx_n_s_nodes, __pyx_n_s_sum_res, __pyx_n_s_node, __pyx_n_s_i); if (unlikely(!__pyx_tuple_)) __PYX_ERR(0, 1, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_tuple_);
  __Pyx_GIVEREF(__pyx_tuple_);
/* … */
  __pyx_t_1 = PyCFunction_NewEx(&__pyx_mdef_10Rcf_cython_1Rcf, NULL, __pyx_n_s_Rcf_cython); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 1, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_1);
  if (PyDict_SetItem(__pyx_d, __pyx_n_s_Rcf, __pyx_t_1) < 0) __PYX_ERR(0, 1, __pyx_L1_error)
  __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;

 02:     """

 03:     Compute numerical approximation using rectangle or mid-point

 04:     method in an interval.

 05:     Nodes are generated via formula: x_i = a+(i+1/2)h_hat for

 06:     i=0,1,...,n-1 and h_hat=(b-a)/n

 07:     Args:

 08:     

 09:         f (float): function expression of integrand.

 10:         

 11:         a (float): left point of interval.

 12:         

 13:         b (float): right point of interval.

 14:         

 15:         n (int): number of subintervals.

 16:         

 17:     Returns:

 18:     

 19:         sum_res (float): numerical approximation to integral

 20:             of f in the interval a,b

 21:     """

+22:     h_hat = (b-a)/n

  __pyx_t_1 = PyNumber_Subtract(__pyx_v_b, __pyx_v_a); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 22, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_1);
  __pyx_t_2 = __Pyx_PyNumber_Divide(__pyx_t_1, __pyx_v_n); if (unlikely(!__pyx_t_2)) __PYX_ERR(0, 22, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_2);
  __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;
  __pyx_v_h_hat = __pyx_t_2;
  __pyx_t_2 = 0;

+23:     nodes = [a+(i+1/2)*h_hat for i in range(n)]

  { /* enter inner scope */
    __pyx_t_2 = PyList_New(0); if (unlikely(!__pyx_t_2)) __PYX_ERR(0, 23, __pyx_L5_error)
    __Pyx_GOTREF(__pyx_t_2);
    __pyx_t_1 = __Pyx_PyObject_CallOneArg(__pyx_builtin_range, __pyx_v_n); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 23, __pyx_L5_error)
    __Pyx_GOTREF(__pyx_t_1);
    if (likely(PyList_CheckExact(__pyx_t_1)) || PyTuple_CheckExact(__pyx_t_1)) {
      __pyx_t_3 = __pyx_t_1; __Pyx_INCREF(__pyx_t_3); __pyx_t_4 = 0;
      __pyx_t_5 = NULL;
    } else {
      __pyx_t_4 = -1; __pyx_t_3 = PyObject_GetIter(__pyx_t_1); if (unlikely(!__pyx_t_3)) __PYX_ERR(0, 23, __pyx_L5_error)
      __Pyx_GOTREF(__pyx_t_3);
      __pyx_t_5 = Py_TYPE(__pyx_t_3)->tp_iternext; if (unlikely(!__pyx_t_5)) __PYX_ERR(0, 23, __pyx_L5_error)
    }
    __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;
    for (;;) {
      if (likely(!__pyx_t_5)) {
        if (likely(PyList_CheckExact(__pyx_t_3))) {
          if (__pyx_t_4 >= PyList_GET_SIZE(__pyx_t_3)) break;
          #if CYTHON_ASSUME_SAFE_MACROS && !CYTHON_AVOID_BORROWED_REFS
          __pyx_t_1 = PyList_GET_ITEM(__pyx_t_3, __pyx_t_4); __Pyx_INCREF(__pyx_t_1); __pyx_t_4++; if (unlikely(0 < 0)) __PYX_ERR(0, 23, __pyx_L5_error)
          #else
          __pyx_t_1 = PySequence_ITEM(__pyx_t_3, __pyx_t_4); __pyx_t_4++; if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 23, __pyx_L5_error)
          __Pyx_GOTREF(__pyx_t_1);
          #endif
        } else {
          if (__pyx_t_4 >= PyTuple_GET_SIZE(__pyx_t_3)) break;
          #if CYTHON_ASSUME_SAFE_MACROS && !CYTHON_AVOID_BORROWED_REFS
          __pyx_t_1 = PyTuple_GET_ITEM(__pyx_t_3, __pyx_t_4); __Pyx_INCREF(__pyx_t_1); __pyx_t_4++; if (unlikely(0 < 0)) __PYX_ERR(0, 23, __pyx_L5_error)
          #else
          __pyx_t_1 = PySequence_ITEM(__pyx_t_3, __pyx_t_4); __pyx_t_4++; if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 23, __pyx_L5_error)
          __Pyx_GOTREF(__pyx_t_1);
          #endif
        }
      } else {
        __pyx_t_1 = __pyx_t_5(__pyx_t_3);
        if (unlikely(!__pyx_t_1)) {
          PyObject* exc_type = PyErr_Occurred();
          if (exc_type) {
            if (likely(__Pyx_PyErr_GivenExceptionMatches(exc_type, PyExc_StopIteration))) PyErr_Clear();
            else __PYX_ERR(0, 23, __pyx_L5_error)
          }
          break;
        }
        __Pyx_GOTREF(__pyx_t_1);
      }
      __Pyx_XDECREF_SET(__pyx_7genexpr__pyx_v_i, __pyx_t_1);
      __pyx_t_1 = 0;
      __pyx_t_1 = PyFloat_FromDouble((1.0 / 2.0)); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 23, __pyx_L5_error)
      __Pyx_GOTREF(__pyx_t_1);
      __pyx_t_6 = PyNumber_Add(__pyx_7genexpr__pyx_v_i, __pyx_t_1); if (unlikely(!__pyx_t_6)) __PYX_ERR(0, 23, __pyx_L5_error)
      __Pyx_GOTREF(__pyx_t_6);
      __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;
      __pyx_t_1 = PyNumber_Multiply(__pyx_t_6, __pyx_v_h_hat); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 23, __pyx_L5_error)
      __Pyx_GOTREF(__pyx_t_1);
      __Pyx_DECREF(__pyx_t_6); __pyx_t_6 = 0;
      __pyx_t_6 = PyNumber_Add(__pyx_v_a, __pyx_t_1); if (unlikely(!__pyx_t_6)) __PYX_ERR(0, 23, __pyx_L5_error)
      __Pyx_GOTREF(__pyx_t_6);
      __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;
      if (unlikely(__Pyx_ListComp_Append(__pyx_t_2, (PyObject*)__pyx_t_6))) __PYX_ERR(0, 23, __pyx_L5_error)
      __Pyx_DECREF(__pyx_t_6); __pyx_t_6 = 0;
    }
    __Pyx_DECREF(__pyx_t_3); __pyx_t_3 = 0;
    __Pyx_XDECREF(__pyx_7genexpr__pyx_v_i); __pyx_7genexpr__pyx_v_i = 0;
    goto __pyx_L8_exit_scope;
    __pyx_L5_error:;
    __Pyx_XDECREF(__pyx_7genexpr__pyx_v_i); __pyx_7genexpr__pyx_v_i = 0;
    goto __pyx_L1_error;
    __pyx_L8_exit_scope:;
  } /* exit inner scope */
  __pyx_v_nodes = ((PyObject*)__pyx_t_2);
  __pyx_t_2 = 0;

+24:     sum_res = 0

  __Pyx_INCREF(__pyx_int_0);
  __pyx_v_sum_res = __pyx_int_0;

+25:     for node in nodes:

  __pyx_t_2 = __pyx_v_nodes; __Pyx_INCREF(__pyx_t_2); __pyx_t_4 = 0;
  for (;;) {
    if (__pyx_t_4 >= PyList_GET_SIZE(__pyx_t_2)) break;
    #if CYTHON_ASSUME_SAFE_MACROS && !CYTHON_AVOID_BORROWED_REFS
    __pyx_t_3 = PyList_GET_ITEM(__pyx_t_2, __pyx_t_4); __Pyx_INCREF(__pyx_t_3); __pyx_t_4++; if (unlikely(0 < 0)) __PYX_ERR(0, 25, __pyx_L1_error)
    #else
    __pyx_t_3 = PySequence_ITEM(__pyx_t_2, __pyx_t_4); __pyx_t_4++; if (unlikely(!__pyx_t_3)) __PYX_ERR(0, 25, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_3);
    #endif
    __Pyx_XDECREF_SET(__pyx_v_node, __pyx_t_3);
    __pyx_t_3 = 0;
/* … */
  }
  __Pyx_DECREF(__pyx_t_2); __pyx_t_2 = 0;

+26:         sum_res = sum_res+f(node)

    __Pyx_INCREF(__pyx_v_f);
    __pyx_t_6 = __pyx_v_f; __pyx_t_1 = NULL;
    if (CYTHON_UNPACK_METHODS && unlikely(PyMethod_Check(__pyx_t_6))) {
      __pyx_t_1 = PyMethod_GET_SELF(__pyx_t_6);
      if (likely(__pyx_t_1)) {
        PyObject* function = PyMethod_GET_FUNCTION(__pyx_t_6);
        __Pyx_INCREF(__pyx_t_1);
        __Pyx_INCREF(function);
        __Pyx_DECREF_SET(__pyx_t_6, function);
      }
    }
    __pyx_t_3 = (__pyx_t_1) ? __Pyx_PyObject_Call2Args(__pyx_t_6, __pyx_t_1, __pyx_v_node) : __Pyx_PyObject_CallOneArg(__pyx_t_6, __pyx_v_node);
    __Pyx_XDECREF(__pyx_t_1); __pyx_t_1 = 0;
    if (unlikely(!__pyx_t_3)) __PYX_ERR(0, 26, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_3);
    __Pyx_DECREF(__pyx_t_6); __pyx_t_6 = 0;
    __pyx_t_6 = PyNumber_Add(__pyx_v_sum_res, __pyx_t_3); if (unlikely(!__pyx_t_6)) __PYX_ERR(0, 26, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_6);
    __Pyx_DECREF(__pyx_t_3); __pyx_t_3 = 0;
    __Pyx_DECREF_SET(__pyx_v_sum_res, __pyx_t_6);
    __pyx_t_6 = 0;

+27:     return h_hat*sum_res

  __Pyx_XDECREF(__pyx_r);
  __pyx_t_2 = PyNumber_Multiply(__pyx_v_h_hat, __pyx_v_sum_res); if (unlikely(!__pyx_t_2)) __PYX_ERR(0, 27, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_2);
  __pyx_r = __pyx_t_2;
  __pyx_t_2 = 0;
  goto __pyx_L0;

Comentarios

Para el código anterior el statement en donde se crean los nodos involucra un loop y es “muy amarilla”. Si se perfila el código se verá que es una línea en la que se gasta una buena parte del tiempo total de ejecución del código.

Una primera opción que tenemos es crear los nodos para el método de integración dentro del loop y separar el llamado a la list comprehension nodes=[a+(i+1/2)*h_hat for i in range(n)]:

%%file Rcf_2_cython.pyx
def Rcf(f,a,b,n):
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
    
        f (float): function expression of integrand.
        
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    h_hat = (b-a)/n
    sum_res = 0
    for i in range(n):
        x = a+(i+1/2)*h_hat
        sum_res += f(x)
    return h_hat*sum_res

Writing Rcf_2_cython.pyx

%%bash
$HOME/.local/bin/cython --force -3 --annotate Rcf_2_cython.pyx

La liga correcta del archivo Rcf_2_cython.c es Rcf_2_cython.c

display(HTML("Rcf_2_cython.html"))

Generated by Cython 0.29.22

Yellow lines hint at Python interaction.
Click on a line that starts with a "+" to see the C code that Cython generated for it.

Raw output: Rcf_2_cython.c

+01: def Rcf(f,a,b,n):

/* Python wrapper */
static PyObject *__pyx_pw_12Rcf_2_cython_1Rcf(PyObject *__pyx_self, PyObject *__pyx_args, PyObject *__pyx_kwds); /*proto*/
static char __pyx_doc_12Rcf_2_cython_Rcf[] = "\n    Compute numerical approximation using rectangle or mid-point\n    method in an interval.\n    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for\n    i=0,1,...,n-1 and h_hat=(b-a)/n\n    Args:\n    \n        f (float): function expression of integrand.\n        \n        a (float): left point of interval.\n        \n        b (float): right point of interval.\n        \n        n (int): number of subintervals.\n        \n    Returns:\n    \n        sum_res (float): numerical approximation to integral\n            of f in the interval a,b\n    ";
static PyMethodDef __pyx_mdef_12Rcf_2_cython_1Rcf = {"Rcf", (PyCFunction)(void*)(PyCFunctionWithKeywords)__pyx_pw_12Rcf_2_cython_1Rcf, METH_VARARGS|METH_KEYWORDS, __pyx_doc_12Rcf_2_cython_Rcf};
static PyObject *__pyx_pw_12Rcf_2_cython_1Rcf(PyObject *__pyx_self, PyObject *__pyx_args, PyObject *__pyx_kwds) {
  PyObject *__pyx_v_f = 0;
  PyObject *__pyx_v_a = 0;
  PyObject *__pyx_v_b = 0;
  PyObject *__pyx_v_n = 0;
  PyObject *__pyx_r = 0;
  __Pyx_RefNannyDeclarations
  __Pyx_RefNannySetupContext("Rcf (wrapper)", 0);
  {
    static PyObject **__pyx_pyargnames[] = {&__pyx_n_s_f,&__pyx_n_s_a,&__pyx_n_s_b,&__pyx_n_s_n,0};
    PyObject* values[4] = {0,0,0,0};
    if (unlikely(__pyx_kwds)) {
      Py_ssize_t kw_args;
      const Py_ssize_t pos_args = PyTuple_GET_SIZE(__pyx_args);
      switch (pos_args) {
        case  4: values[3] = PyTuple_GET_ITEM(__pyx_args, 3);
        CYTHON_FALLTHROUGH;
        case  3: values[2] = PyTuple_GET_ITEM(__pyx_args, 2);
        CYTHON_FALLTHROUGH;
        case  2: values[1] = PyTuple_GET_ITEM(__pyx_args, 1);
        CYTHON_FALLTHROUGH;
        case  1: values[0] = PyTuple_GET_ITEM(__pyx_args, 0);
        CYTHON_FALLTHROUGH;
        case  0: break;
        default: goto __pyx_L5_argtuple_error;
      }
      kw_args = PyDict_Size(__pyx_kwds);
      switch (pos_args) {
        case  0:
        if (likely((values[0] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_f)) != 0)) kw_args--;
        else goto __pyx_L5_argtuple_error;
        CYTHON_FALLTHROUGH;
        case  1:
        if (likely((values[1] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_a)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 4, 4, 1); __PYX_ERR(0, 1, __pyx_L3_error)
        }
        CYTHON_FALLTHROUGH;
        case  2:
        if (likely((values[2] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_b)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 4, 4, 2); __PYX_ERR(0, 1, __pyx_L3_error)
        }
        CYTHON_FALLTHROUGH;
        case  3:
        if (likely((values[3] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_n)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 4, 4, 3); __PYX_ERR(0, 1, __pyx_L3_error)
        }
      }
      if (unlikely(kw_args > 0)) {
        if (unlikely(__Pyx_ParseOptionalKeywords(__pyx_kwds, __pyx_pyargnames, 0, values, pos_args, "Rcf") < 0)) __PYX_ERR(0, 1, __pyx_L3_error)
      }
    } else if (PyTuple_GET_SIZE(__pyx_args) != 4) {
      goto __pyx_L5_argtuple_error;
    } else {
      values[0] = PyTuple_GET_ITEM(__pyx_args, 0);
      values[1] = PyTuple_GET_ITEM(__pyx_args, 1);
      values[2] = PyTuple_GET_ITEM(__pyx_args, 2);
      values[3] = PyTuple_GET_ITEM(__pyx_args, 3);
    }
    __pyx_v_f = values[0];
    __pyx_v_a = values[1];
    __pyx_v_b = values[2];
    __pyx_v_n = values[3];
  }
  goto __pyx_L4_argument_unpacking_done;
  __pyx_L5_argtuple_error:;
  __Pyx_RaiseArgtupleInvalid("Rcf", 1, 4, 4, PyTuple_GET_SIZE(__pyx_args)); __PYX_ERR(0, 1, __pyx_L3_error)
  __pyx_L3_error:;
  __Pyx_AddTraceback("Rcf_2_cython.Rcf", __pyx_clineno, __pyx_lineno, __pyx_filename);
  __Pyx_RefNannyFinishContext();
  return NULL;
  __pyx_L4_argument_unpacking_done:;
  __pyx_r = __pyx_pf_12Rcf_2_cython_Rcf(__pyx_self, __pyx_v_f, __pyx_v_a, __pyx_v_b, __pyx_v_n);
  int __pyx_lineno = 0;
  const char *__pyx_filename = NULL;
  int __pyx_clineno = 0;

  /* function exit code */
  __Pyx_RefNannyFinishContext();
  return __pyx_r;
}

static PyObject *__pyx_pf_12Rcf_2_cython_Rcf(CYTHON_UNUSED PyObject *__pyx_self, PyObject *__pyx_v_f, PyObject *__pyx_v_a, PyObject *__pyx_v_b, PyObject *__pyx_v_n) {
  PyObject *__pyx_v_h_hat = NULL;
  PyObject *__pyx_v_sum_res = NULL;
  PyObject *__pyx_v_i = NULL;
  PyObject *__pyx_v_x = NULL;
  PyObject *__pyx_r = NULL;
  __Pyx_RefNannyDeclarations
  __Pyx_RefNannySetupContext("Rcf", 0);
/* … */
  /* function exit code */
  __pyx_L1_error:;
  __Pyx_XDECREF(__pyx_t_1);
  __Pyx_XDECREF(__pyx_t_2);
  __Pyx_XDECREF(__pyx_t_5);
  __Pyx_XDECREF(__pyx_t_6);
  __Pyx_AddTraceback("Rcf_2_cython.Rcf", __pyx_clineno, __pyx_lineno, __pyx_filename);
  __pyx_r = NULL;
  __pyx_L0:;
  __Pyx_XDECREF(__pyx_v_h_hat);
  __Pyx_XDECREF(__pyx_v_sum_res);
  __Pyx_XDECREF(__pyx_v_i);
  __Pyx_XDECREF(__pyx_v_x);
  __Pyx_XGIVEREF(__pyx_r);
  __Pyx_RefNannyFinishContext();
  return __pyx_r;
}
/* … */
  __pyx_tuple_ = PyTuple_Pack(8, __pyx_n_s_f, __pyx_n_s_a, __pyx_n_s_b, __pyx_n_s_n, __pyx_n_s_h_hat, __pyx_n_s_sum_res, __pyx_n_s_i, __pyx_n_s_x); if (unlikely(!__pyx_tuple_)) __PYX_ERR(0, 1, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_tuple_);
  __Pyx_GIVEREF(__pyx_tuple_);
/* … */
  __pyx_t_1 = PyCFunction_NewEx(&__pyx_mdef_12Rcf_2_cython_1Rcf, NULL, __pyx_n_s_Rcf_2_cython); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 1, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_1);
  if (PyDict_SetItem(__pyx_d, __pyx_n_s_Rcf, __pyx_t_1) < 0) __PYX_ERR(0, 1, __pyx_L1_error)
  __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;

 02:     """

 03:     Compute numerical approximation using rectangle or mid-point

 04:     method in an interval.

 05:     Nodes are generated via formula: x_i = a+(i+1/2)h_hat for

 06:     i=0,1,...,n-1 and h_hat=(b-a)/n

 07:     Args:

 08:     

 09:         f (float): function expression of integrand.

 10:         

 11:         a (float): left point of interval.

 12:         

 13:         b (float): right point of interval.

 14:         

 15:         n (int): number of subintervals.

 16:         

 17:     Returns:

 18:     

 19:         sum_res (float): numerical approximation to integral

 20:             of f in the interval a,b

 21:     """

+22:     h_hat = (b-a)/n

  __pyx_t_1 = PyNumber_Subtract(__pyx_v_b, __pyx_v_a); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 22, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_1);
  __pyx_t_2 = __Pyx_PyNumber_Divide(__pyx_t_1, __pyx_v_n); if (unlikely(!__pyx_t_2)) __PYX_ERR(0, 22, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_2);
  __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;
  __pyx_v_h_hat = __pyx_t_2;
  __pyx_t_2 = 0;

+23:     sum_res = 0

  __Pyx_INCREF(__pyx_int_0);
  __pyx_v_sum_res = __pyx_int_0;

+24:     for i in range(n):

  __pyx_t_2 = __Pyx_PyObject_CallOneArg(__pyx_builtin_range, __pyx_v_n); if (unlikely(!__pyx_t_2)) __PYX_ERR(0, 24, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_2);
  if (likely(PyList_CheckExact(__pyx_t_2)) || PyTuple_CheckExact(__pyx_t_2)) {
    __pyx_t_1 = __pyx_t_2; __Pyx_INCREF(__pyx_t_1); __pyx_t_3 = 0;
    __pyx_t_4 = NULL;
  } else {
    __pyx_t_3 = -1; __pyx_t_1 = PyObject_GetIter(__pyx_t_2); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 24, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_1);
    __pyx_t_4 = Py_TYPE(__pyx_t_1)->tp_iternext; if (unlikely(!__pyx_t_4)) __PYX_ERR(0, 24, __pyx_L1_error)
  }
  __Pyx_DECREF(__pyx_t_2); __pyx_t_2 = 0;
  for (;;) {
    if (likely(!__pyx_t_4)) {
      if (likely(PyList_CheckExact(__pyx_t_1))) {
        if (__pyx_t_3 >= PyList_GET_SIZE(__pyx_t_1)) break;
        #if CYTHON_ASSUME_SAFE_MACROS && !CYTHON_AVOID_BORROWED_REFS
        __pyx_t_2 = PyList_GET_ITEM(__pyx_t_1, __pyx_t_3); __Pyx_INCREF(__pyx_t_2); __pyx_t_3++; if (unlikely(0 < 0)) __PYX_ERR(0, 24, __pyx_L1_error)
        #else
        __pyx_t_2 = PySequence_ITEM(__pyx_t_1, __pyx_t_3); __pyx_t_3++; if (unlikely(!__pyx_t_2)) __PYX_ERR(0, 24, __pyx_L1_error)
        __Pyx_GOTREF(__pyx_t_2);
        #endif
      } else {
        if (__pyx_t_3 >= PyTuple_GET_SIZE(__pyx_t_1)) break;
        #if CYTHON_ASSUME_SAFE_MACROS && !CYTHON_AVOID_BORROWED_REFS
        __pyx_t_2 = PyTuple_GET_ITEM(__pyx_t_1, __pyx_t_3); __Pyx_INCREF(__pyx_t_2); __pyx_t_3++; if (unlikely(0 < 0)) __PYX_ERR(0, 24, __pyx_L1_error)
        #else
        __pyx_t_2 = PySequence_ITEM(__pyx_t_1, __pyx_t_3); __pyx_t_3++; if (unlikely(!__pyx_t_2)) __PYX_ERR(0, 24, __pyx_L1_error)
        __Pyx_GOTREF(__pyx_t_2);
        #endif
      }
    } else {
      __pyx_t_2 = __pyx_t_4(__pyx_t_1);
      if (unlikely(!__pyx_t_2)) {
        PyObject* exc_type = PyErr_Occurred();
        if (exc_type) {
          if (likely(__Pyx_PyErr_GivenExceptionMatches(exc_type, PyExc_StopIteration))) PyErr_Clear();
          else __PYX_ERR(0, 24, __pyx_L1_error)
        }
        break;
      }
      __Pyx_GOTREF(__pyx_t_2);
    }
    __Pyx_XDECREF_SET(__pyx_v_i, __pyx_t_2);
    __pyx_t_2 = 0;
/* … */
  }
  __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;

+25:         x = a+(i+1/2)*h_hat

    __pyx_t_2 = PyFloat_FromDouble((1.0 / 2.0)); if (unlikely(!__pyx_t_2)) __PYX_ERR(0, 25, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_2);
    __pyx_t_5 = PyNumber_Add(__pyx_v_i, __pyx_t_2); if (unlikely(!__pyx_t_5)) __PYX_ERR(0, 25, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_5);
    __Pyx_DECREF(__pyx_t_2); __pyx_t_2 = 0;
    __pyx_t_2 = PyNumber_Multiply(__pyx_t_5, __pyx_v_h_hat); if (unlikely(!__pyx_t_2)) __PYX_ERR(0, 25, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_2);
    __Pyx_DECREF(__pyx_t_5); __pyx_t_5 = 0;
    __pyx_t_5 = PyNumber_Add(__pyx_v_a, __pyx_t_2); if (unlikely(!__pyx_t_5)) __PYX_ERR(0, 25, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_5);
    __Pyx_DECREF(__pyx_t_2); __pyx_t_2 = 0;
    __Pyx_XDECREF_SET(__pyx_v_x, __pyx_t_5);
    __pyx_t_5 = 0;

+26:         sum_res += f(x)

    __Pyx_INCREF(__pyx_v_f);
    __pyx_t_2 = __pyx_v_f; __pyx_t_6 = NULL;
    if (CYTHON_UNPACK_METHODS && unlikely(PyMethod_Check(__pyx_t_2))) {
      __pyx_t_6 = PyMethod_GET_SELF(__pyx_t_2);
      if (likely(__pyx_t_6)) {
        PyObject* function = PyMethod_GET_FUNCTION(__pyx_t_2);
        __Pyx_INCREF(__pyx_t_6);
        __Pyx_INCREF(function);
        __Pyx_DECREF_SET(__pyx_t_2, function);
      }
    }
    __pyx_t_5 = (__pyx_t_6) ? __Pyx_PyObject_Call2Args(__pyx_t_2, __pyx_t_6, __pyx_v_x) : __Pyx_PyObject_CallOneArg(__pyx_t_2, __pyx_v_x);
    __Pyx_XDECREF(__pyx_t_6); __pyx_t_6 = 0;
    if (unlikely(!__pyx_t_5)) __PYX_ERR(0, 26, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_5);
    __Pyx_DECREF(__pyx_t_2); __pyx_t_2 = 0;
    __pyx_t_2 = PyNumber_InPlaceAdd(__pyx_v_sum_res, __pyx_t_5); if (unlikely(!__pyx_t_2)) __PYX_ERR(0, 26, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_2);
    __Pyx_DECREF(__pyx_t_5); __pyx_t_5 = 0;
    __Pyx_DECREF_SET(__pyx_v_sum_res, __pyx_t_2);
    __pyx_t_2 = 0;

+27:     return h_hat*sum_res

  __Pyx_XDECREF(__pyx_r);
  __pyx_t_1 = PyNumber_Multiply(__pyx_v_h_hat, __pyx_v_sum_res); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 27, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_1);
  __pyx_r = __pyx_t_1;
  __pyx_t_1 = 0;
  goto __pyx_L0;

Comentario

Para el código anterior los statements que están dentro del loop son “muy amarillos”. En tales statements involucran tipos de valores que no cambiarán en la ejecución de cada loop. Una opción es declarar los tipos de objetos que están involucrados en el loop utilizando la sintaxis cdef. Ver function_declarations, definition-of-def-cdef-and-cpdef-in-cython

%%file Rcf_3_cython.pyx
def Rcf(f, double a, double b, unsigned int n):
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
    
        f (float): function expression of integrand.
        
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    cdef unsigned int i
    cdef double x, sum_res, h_hat
    h_hat = (b-a)/n
    sum_res = 0
    for i in range(n):
        x = a+(i+1/2)*h_hat
        sum_res += f(x)
    return h_hat*sum_res

Writing Rcf_3_cython.pyx

%%bash
$HOME/.local/bin/cython -3 --force --annotate Rcf_3_cython.pyx

La liga correcta del archivo Rcf_3_cython.c es Rcf_3_cython.c

display(HTML("Rcf_3_cython.html"))

Generated by Cython 0.29.22

Yellow lines hint at Python interaction.
Click on a line that starts with a "+" to see the C code that Cython generated for it.

Raw output: Rcf_3_cython.c

+01: def Rcf(f, double a, double b, unsigned int n):

/* Python wrapper */
static PyObject *__pyx_pw_12Rcf_3_cython_1Rcf(PyObject *__pyx_self, PyObject *__pyx_args, PyObject *__pyx_kwds); /*proto*/
static char __pyx_doc_12Rcf_3_cython_Rcf[] = "\n    Compute numerical approximation using rectangle or mid-point\n    method in an interval.\n    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for\n    i=0,1,...,n-1 and h_hat=(b-a)/n\n    Args:\n    \n        f (float): function expression of integrand.\n        \n        a (float): left point of interval.\n        \n        b (float): right point of interval.\n        \n        n (int): number of subintervals.\n        \n    Returns:\n    \n        sum_res (float): numerical approximation to integral\n            of f in the interval a,b\n    ";
static PyMethodDef __pyx_mdef_12Rcf_3_cython_1Rcf = {"Rcf", (PyCFunction)(void*)(PyCFunctionWithKeywords)__pyx_pw_12Rcf_3_cython_1Rcf, METH_VARARGS|METH_KEYWORDS, __pyx_doc_12Rcf_3_cython_Rcf};
static PyObject *__pyx_pw_12Rcf_3_cython_1Rcf(PyObject *__pyx_self, PyObject *__pyx_args, PyObject *__pyx_kwds) {
  PyObject *__pyx_v_f = 0;
  double __pyx_v_a;
  double __pyx_v_b;
  unsigned int __pyx_v_n;
  PyObject *__pyx_r = 0;
  __Pyx_RefNannyDeclarations
  __Pyx_RefNannySetupContext("Rcf (wrapper)", 0);
  {
    static PyObject **__pyx_pyargnames[] = {&__pyx_n_s_f,&__pyx_n_s_a,&__pyx_n_s_b,&__pyx_n_s_n,0};
    PyObject* values[4] = {0,0,0,0};
    if (unlikely(__pyx_kwds)) {
      Py_ssize_t kw_args;
      const Py_ssize_t pos_args = PyTuple_GET_SIZE(__pyx_args);
      switch (pos_args) {
        case  4: values[3] = PyTuple_GET_ITEM(__pyx_args, 3);
        CYTHON_FALLTHROUGH;
        case  3: values[2] = PyTuple_GET_ITEM(__pyx_args, 2);
        CYTHON_FALLTHROUGH;
        case  2: values[1] = PyTuple_GET_ITEM(__pyx_args, 1);
        CYTHON_FALLTHROUGH;
        case  1: values[0] = PyTuple_GET_ITEM(__pyx_args, 0);
        CYTHON_FALLTHROUGH;
        case  0: break;
        default: goto __pyx_L5_argtuple_error;
      }
      kw_args = PyDict_Size(__pyx_kwds);
      switch (pos_args) {
        case  0:
        if (likely((values[0] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_f)) != 0)) kw_args--;
        else goto __pyx_L5_argtuple_error;
        CYTHON_FALLTHROUGH;
        case  1:
        if (likely((values[1] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_a)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 4, 4, 1); __PYX_ERR(0, 1, __pyx_L3_error)
        }
        CYTHON_FALLTHROUGH;
        case  2:
        if (likely((values[2] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_b)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 4, 4, 2); __PYX_ERR(0, 1, __pyx_L3_error)
        }
        CYTHON_FALLTHROUGH;
        case  3:
        if (likely((values[3] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_n)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 4, 4, 3); __PYX_ERR(0, 1, __pyx_L3_error)
        }
      }
      if (unlikely(kw_args > 0)) {
        if (unlikely(__Pyx_ParseOptionalKeywords(__pyx_kwds, __pyx_pyargnames, 0, values, pos_args, "Rcf") < 0)) __PYX_ERR(0, 1, __pyx_L3_error)
      }
    } else if (PyTuple_GET_SIZE(__pyx_args) != 4) {
      goto __pyx_L5_argtuple_error;
    } else {
      values[0] = PyTuple_GET_ITEM(__pyx_args, 0);
      values[1] = PyTuple_GET_ITEM(__pyx_args, 1);
      values[2] = PyTuple_GET_ITEM(__pyx_args, 2);
      values[3] = PyTuple_GET_ITEM(__pyx_args, 3);
    }
    __pyx_v_f = values[0];
    __pyx_v_a = __pyx_PyFloat_AsDouble(values[1]); if (unlikely((__pyx_v_a == (double)-1) && PyErr_Occurred())) __PYX_ERR(0, 1, __pyx_L3_error)
    __pyx_v_b = __pyx_PyFloat_AsDouble(values[2]); if (unlikely((__pyx_v_b == (double)-1) && PyErr_Occurred())) __PYX_ERR(0, 1, __pyx_L3_error)
    __pyx_v_n = __Pyx_PyInt_As_unsigned_int(values[3]); if (unlikely((__pyx_v_n == (unsigned int)-1) && PyErr_Occurred())) __PYX_ERR(0, 1, __pyx_L3_error)
  }
  goto __pyx_L4_argument_unpacking_done;
  __pyx_L5_argtuple_error:;
  __Pyx_RaiseArgtupleInvalid("Rcf", 1, 4, 4, PyTuple_GET_SIZE(__pyx_args)); __PYX_ERR(0, 1, __pyx_L3_error)
  __pyx_L3_error:;
  __Pyx_AddTraceback("Rcf_3_cython.Rcf", __pyx_clineno, __pyx_lineno, __pyx_filename);
  __Pyx_RefNannyFinishContext();
  return NULL;
  __pyx_L4_argument_unpacking_done:;
  __pyx_r = __pyx_pf_12Rcf_3_cython_Rcf(__pyx_self, __pyx_v_f, __pyx_v_a, __pyx_v_b, __pyx_v_n);
  int __pyx_lineno = 0;
  const char *__pyx_filename = NULL;
  int __pyx_clineno = 0;

  /* function exit code */
  __Pyx_RefNannyFinishContext();
  return __pyx_r;
}

static PyObject *__pyx_pf_12Rcf_3_cython_Rcf(CYTHON_UNUSED PyObject *__pyx_self, PyObject *__pyx_v_f, double __pyx_v_a, double __pyx_v_b, unsigned int __pyx_v_n) {
  unsigned int __pyx_v_i;
  double __pyx_v_x;
  double __pyx_v_sum_res;
  double __pyx_v_h_hat;
  PyObject *__pyx_r = NULL;
  __Pyx_RefNannyDeclarations
  __Pyx_RefNannySetupContext("Rcf", 0);
/* … */
  /* function exit code */
  __pyx_L1_error:;
  __Pyx_XDECREF(__pyx_t_5);
  __Pyx_XDECREF(__pyx_t_6);
  __Pyx_XDECREF(__pyx_t_7);
  __Pyx_XDECREF(__pyx_t_8);
  __Pyx_XDECREF(__pyx_t_9);
  __Pyx_AddTraceback("Rcf_3_cython.Rcf", __pyx_clineno, __pyx_lineno, __pyx_filename);
  __pyx_r = NULL;
  __pyx_L0:;
  __Pyx_XGIVEREF(__pyx_r);
  __Pyx_RefNannyFinishContext();
  return __pyx_r;
}
/* … */
  __pyx_tuple_ = PyTuple_Pack(8, __pyx_n_s_f, __pyx_n_s_a, __pyx_n_s_b, __pyx_n_s_n, __pyx_n_s_i, __pyx_n_s_x, __pyx_n_s_sum_res, __pyx_n_s_h_hat); if (unlikely(!__pyx_tuple_)) __PYX_ERR(0, 1, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_tuple_);
  __Pyx_GIVEREF(__pyx_tuple_);
/* … */
  __pyx_t_1 = PyCFunction_NewEx(&__pyx_mdef_12Rcf_3_cython_1Rcf, NULL, __pyx_n_s_Rcf_3_cython); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 1, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_1);
  if (PyDict_SetItem(__pyx_d, __pyx_n_s_Rcf, __pyx_t_1) < 0) __PYX_ERR(0, 1, __pyx_L1_error)
  __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;

 02:     """

 03:     Compute numerical approximation using rectangle or mid-point

 04:     method in an interval.

 05:     Nodes are generated via formula: x_i = a+(i+1/2)h_hat for

 06:     i=0,1,...,n-1 and h_hat=(b-a)/n

 07:     Args:

 08:     

 09:         f (float): function expression of integrand.

 10:         

 11:         a (float): left point of interval.

 12:         

 13:         b (float): right point of interval.

 14:         

 15:         n (int): number of subintervals.

 16:         

 17:     Returns:

 18:     

 19:         sum_res (float): numerical approximation to integral

 20:             of f in the interval a,b

 21:     """

 22:     cdef unsigned int i

 23:     cdef double x, sum_res, h_hat

+24:     h_hat = (b-a)/n

  __pyx_t_1 = (__pyx_v_b - __pyx_v_a);
  if (unlikely(__pyx_v_n == 0)) {
    PyErr_SetString(PyExc_ZeroDivisionError, "float division");
    __PYX_ERR(0, 24, __pyx_L1_error)
  }
  __pyx_v_h_hat = (__pyx_t_1 / ((double)__pyx_v_n));

+25:     sum_res = 0

  __pyx_v_sum_res = 0.0;

+26:     for i in range(n):

  __pyx_t_2 = __pyx_v_n;
  __pyx_t_3 = __pyx_t_2;
  for (__pyx_t_4 = 0; __pyx_t_4 < __pyx_t_3; __pyx_t_4+=1) {
    __pyx_v_i = __pyx_t_4;

+27:         x = a+(i+1/2)*h_hat

    __pyx_v_x = (__pyx_v_a + ((__pyx_v_i + (1.0 / 2.0)) * __pyx_v_h_hat));

+28:         sum_res += f(x)

    __pyx_t_5 = PyFloat_FromDouble(__pyx_v_sum_res); if (unlikely(!__pyx_t_5)) __PYX_ERR(0, 28, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_5);
    __pyx_t_7 = PyFloat_FromDouble(__pyx_v_x); if (unlikely(!__pyx_t_7)) __PYX_ERR(0, 28, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_7);
    __Pyx_INCREF(__pyx_v_f);
    __pyx_t_8 = __pyx_v_f; __pyx_t_9 = NULL;
    if (CYTHON_UNPACK_METHODS && unlikely(PyMethod_Check(__pyx_t_8))) {
      __pyx_t_9 = PyMethod_GET_SELF(__pyx_t_8);
      if (likely(__pyx_t_9)) {
        PyObject* function = PyMethod_GET_FUNCTION(__pyx_t_8);
        __Pyx_INCREF(__pyx_t_9);
        __Pyx_INCREF(function);
        __Pyx_DECREF_SET(__pyx_t_8, function);
      }
    }
    __pyx_t_6 = (__pyx_t_9) ? __Pyx_PyObject_Call2Args(__pyx_t_8, __pyx_t_9, __pyx_t_7) : __Pyx_PyObject_CallOneArg(__pyx_t_8, __pyx_t_7);
    __Pyx_XDECREF(__pyx_t_9); __pyx_t_9 = 0;
    __Pyx_DECREF(__pyx_t_7); __pyx_t_7 = 0;
    if (unlikely(!__pyx_t_6)) __PYX_ERR(0, 28, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_6);
    __Pyx_DECREF(__pyx_t_8); __pyx_t_8 = 0;
    __pyx_t_8 = PyNumber_InPlaceAdd(__pyx_t_5, __pyx_t_6); if (unlikely(!__pyx_t_8)) __PYX_ERR(0, 28, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_8);
    __Pyx_DECREF(__pyx_t_5); __pyx_t_5 = 0;
    __Pyx_DECREF(__pyx_t_6); __pyx_t_6 = 0;
    __pyx_t_1 = __pyx_PyFloat_AsDouble(__pyx_t_8); if (unlikely((__pyx_t_1 == (double)-1) && PyErr_Occurred())) __PYX_ERR(0, 28, __pyx_L1_error)
    __Pyx_DECREF(__pyx_t_8); __pyx_t_8 = 0;
    __pyx_v_sum_res = __pyx_t_1;
  }

+29:     return h_hat*sum_res

  __Pyx_XDECREF(__pyx_r);
  __pyx_t_8 = PyFloat_FromDouble((__pyx_v_h_hat * __pyx_v_sum_res)); if (unlikely(!__pyx_t_8)) __PYX_ERR(0, 29, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_8);
  __pyx_r = __pyx_t_8;
  __pyx_t_8 = 0;
  goto __pyx_L0;

Comentario

Al definir tipos, éstos sólo serán entendidos por Cython y no por Python. Cython utiliza estos tipos para convertir el código de Python a código de C.

Una opción con la que perdemos flexibilidad pero ganamos en disminuir tiempo de ejecución es directamente llamar a la función math.exp:

%%file Rcf_4_cython.pyx
import math
def Rcf(double a, double b, unsigned int n):
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
    
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    cdef unsigned int i
    cdef double x, sum_res, h_hat
    h_hat = (b-a)/n
    sum_res = 0
    for i in range(n):
        x = a+(i+1/2)*h_hat
        sum_res += math.exp(-x**2)
    return h_hat*sum_res

Writing Rcf_4_cython.pyx

%%bash
$HOME/.local/bin/cython -3 --force --annotate Rcf_4_cython.pyx

La liga correcta del archivo Rcf_4_cython.c es Rcf_4_cython.c

display(HTML("Rcf_4_cython.html"))

Generated by Cython 0.29.22

Yellow lines hint at Python interaction.
Click on a line that starts with a "+" to see the C code that Cython generated for it.

Raw output: Rcf_4_cython.c

+01: import math

  __pyx_t_1 = __Pyx_Import(__pyx_n_s_math, 0, 0); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 1, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_1);
  if (PyDict_SetItem(__pyx_d, __pyx_n_s_math, __pyx_t_1) < 0) __PYX_ERR(0, 1, __pyx_L1_error)
  __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;

+02: def Rcf(double a, double b, unsigned int n):

/* Python wrapper */
static PyObject *__pyx_pw_12Rcf_4_cython_1Rcf(PyObject *__pyx_self, PyObject *__pyx_args, PyObject *__pyx_kwds); /*proto*/
static char __pyx_doc_12Rcf_4_cython_Rcf[] = "\n    Compute numerical approximation using rectangle or mid-point\n    method in an interval.\n    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for\n    i=0,1,...,n-1 and h_hat=(b-a)/n\n    Args:\n    \n        a (float): left point of interval.\n        \n        b (float): right point of interval.\n        \n        n (int): number of subintervals.\n        \n    Returns:\n    \n        sum_res (float): numerical approximation to integral\n            of f in the interval a,b\n    ";
static PyMethodDef __pyx_mdef_12Rcf_4_cython_1Rcf = {"Rcf", (PyCFunction)(void*)(PyCFunctionWithKeywords)__pyx_pw_12Rcf_4_cython_1Rcf, METH_VARARGS|METH_KEYWORDS, __pyx_doc_12Rcf_4_cython_Rcf};
static PyObject *__pyx_pw_12Rcf_4_cython_1Rcf(PyObject *__pyx_self, PyObject *__pyx_args, PyObject *__pyx_kwds) {
  double __pyx_v_a;
  double __pyx_v_b;
  unsigned int __pyx_v_n;
  PyObject *__pyx_r = 0;
  __Pyx_RefNannyDeclarations
  __Pyx_RefNannySetupContext("Rcf (wrapper)", 0);
  {
    static PyObject **__pyx_pyargnames[] = {&__pyx_n_s_a,&__pyx_n_s_b,&__pyx_n_s_n,0};
    PyObject* values[3] = {0,0,0};
    if (unlikely(__pyx_kwds)) {
      Py_ssize_t kw_args;
      const Py_ssize_t pos_args = PyTuple_GET_SIZE(__pyx_args);
      switch (pos_args) {
        case  3: values[2] = PyTuple_GET_ITEM(__pyx_args, 2);
        CYTHON_FALLTHROUGH;
        case  2: values[1] = PyTuple_GET_ITEM(__pyx_args, 1);
        CYTHON_FALLTHROUGH;
        case  1: values[0] = PyTuple_GET_ITEM(__pyx_args, 0);
        CYTHON_FALLTHROUGH;
        case  0: break;
        default: goto __pyx_L5_argtuple_error;
      }
      kw_args = PyDict_Size(__pyx_kwds);
      switch (pos_args) {
        case  0:
        if (likely((values[0] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_a)) != 0)) kw_args--;
        else goto __pyx_L5_argtuple_error;
        CYTHON_FALLTHROUGH;
        case  1:
        if (likely((values[1] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_b)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 3, 3, 1); __PYX_ERR(0, 2, __pyx_L3_error)
        }
        CYTHON_FALLTHROUGH;
        case  2:
        if (likely((values[2] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_n)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 3, 3, 2); __PYX_ERR(0, 2, __pyx_L3_error)
        }
      }
      if (unlikely(kw_args > 0)) {
        if (unlikely(__Pyx_ParseOptionalKeywords(__pyx_kwds, __pyx_pyargnames, 0, values, pos_args, "Rcf") < 0)) __PYX_ERR(0, 2, __pyx_L3_error)
      }
    } else if (PyTuple_GET_SIZE(__pyx_args) != 3) {
      goto __pyx_L5_argtuple_error;
    } else {
      values[0] = PyTuple_GET_ITEM(__pyx_args, 0);
      values[1] = PyTuple_GET_ITEM(__pyx_args, 1);
      values[2] = PyTuple_GET_ITEM(__pyx_args, 2);
    }
    __pyx_v_a = __pyx_PyFloat_AsDouble(values[0]); if (unlikely((__pyx_v_a == (double)-1) && PyErr_Occurred())) __PYX_ERR(0, 2, __pyx_L3_error)
    __pyx_v_b = __pyx_PyFloat_AsDouble(values[1]); if (unlikely((__pyx_v_b == (double)-1) && PyErr_Occurred())) __PYX_ERR(0, 2, __pyx_L3_error)
    __pyx_v_n = __Pyx_PyInt_As_unsigned_int(values[2]); if (unlikely((__pyx_v_n == (unsigned int)-1) && PyErr_Occurred())) __PYX_ERR(0, 2, __pyx_L3_error)
  }
  goto __pyx_L4_argument_unpacking_done;
  __pyx_L5_argtuple_error:;
  __Pyx_RaiseArgtupleInvalid("Rcf", 1, 3, 3, PyTuple_GET_SIZE(__pyx_args)); __PYX_ERR(0, 2, __pyx_L3_error)
  __pyx_L3_error:;
  __Pyx_AddTraceback("Rcf_4_cython.Rcf", __pyx_clineno, __pyx_lineno, __pyx_filename);
  __Pyx_RefNannyFinishContext();
  return NULL;
  __pyx_L4_argument_unpacking_done:;
  __pyx_r = __pyx_pf_12Rcf_4_cython_Rcf(__pyx_self, __pyx_v_a, __pyx_v_b, __pyx_v_n);
  int __pyx_lineno = 0;
  const char *__pyx_filename = NULL;
  int __pyx_clineno = 0;

  /* function exit code */
  __Pyx_RefNannyFinishContext();
  return __pyx_r;
}

static PyObject *__pyx_pf_12Rcf_4_cython_Rcf(CYTHON_UNUSED PyObject *__pyx_self, double __pyx_v_a, double __pyx_v_b, unsigned int __pyx_v_n) {
  unsigned int __pyx_v_i;
  double __pyx_v_x;
  double __pyx_v_sum_res;
  double __pyx_v_h_hat;
  PyObject *__pyx_r = NULL;
  __Pyx_RefNannyDeclarations
  __Pyx_RefNannySetupContext("Rcf", 0);
/* … */
  /* function exit code */
  __pyx_L1_error:;
  __Pyx_XDECREF(__pyx_t_5);
  __Pyx_XDECREF(__pyx_t_6);
  __Pyx_XDECREF(__pyx_t_7);
  __Pyx_XDECREF(__pyx_t_8);
  __Pyx_XDECREF(__pyx_t_9);
  __Pyx_AddTraceback("Rcf_4_cython.Rcf", __pyx_clineno, __pyx_lineno, __pyx_filename);
  __pyx_r = NULL;
  __pyx_L0:;
  __Pyx_XGIVEREF(__pyx_r);
  __Pyx_RefNannyFinishContext();
  return __pyx_r;
}
/* … */
  __pyx_tuple_ = PyTuple_Pack(7, __pyx_n_s_a, __pyx_n_s_b, __pyx_n_s_n, __pyx_n_s_i, __pyx_n_s_x, __pyx_n_s_sum_res, __pyx_n_s_h_hat); if (unlikely(!__pyx_tuple_)) __PYX_ERR(0, 2, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_tuple_);
  __Pyx_GIVEREF(__pyx_tuple_);
/* … */
  __pyx_t_1 = PyCFunction_NewEx(&__pyx_mdef_12Rcf_4_cython_1Rcf, NULL, __pyx_n_s_Rcf_4_cython); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 2, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_1);
  if (PyDict_SetItem(__pyx_d, __pyx_n_s_Rcf, __pyx_t_1) < 0) __PYX_ERR(0, 2, __pyx_L1_error)
  __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;

 03:     """

 04:     Compute numerical approximation using rectangle or mid-point

 05:     method in an interval.

 06:     Nodes are generated via formula: x_i = a+(i+1/2)h_hat for

 07:     i=0,1,...,n-1 and h_hat=(b-a)/n

 08:     Args:

 09:     

 10:         a (float): left point of interval.

 11:         

 12:         b (float): right point of interval.

 13:         

 14:         n (int): number of subintervals.

 15:         

 16:     Returns:

 17:     

 18:         sum_res (float): numerical approximation to integral

 19:             of f in the interval a,b

 20:     """

 21:     cdef unsigned int i

 22:     cdef double x, sum_res, h_hat

+23:     h_hat = (b-a)/n

  __pyx_t_1 = (__pyx_v_b - __pyx_v_a);
  if (unlikely(__pyx_v_n == 0)) {
    PyErr_SetString(PyExc_ZeroDivisionError, "float division");
    __PYX_ERR(0, 23, __pyx_L1_error)
  }
  __pyx_v_h_hat = (__pyx_t_1 / ((double)__pyx_v_n));

+24:     sum_res = 0

  __pyx_v_sum_res = 0.0;

+25:     for i in range(n):

  __pyx_t_2 = __pyx_v_n;
  __pyx_t_3 = __pyx_t_2;
  for (__pyx_t_4 = 0; __pyx_t_4 < __pyx_t_3; __pyx_t_4+=1) {
    __pyx_v_i = __pyx_t_4;

+26:         x = a+(i+1/2)*h_hat

    __pyx_v_x = (__pyx_v_a + ((__pyx_v_i + (1.0 / 2.0)) * __pyx_v_h_hat));

+27:         sum_res += math.exp(-x**2)

    __pyx_t_5 = PyFloat_FromDouble(__pyx_v_sum_res); if (unlikely(!__pyx_t_5)) __PYX_ERR(0, 27, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_5);
    __Pyx_GetModuleGlobalName(__pyx_t_7, __pyx_n_s_math); if (unlikely(!__pyx_t_7)) __PYX_ERR(0, 27, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_7);
    __pyx_t_8 = __Pyx_PyObject_GetAttrStr(__pyx_t_7, __pyx_n_s_exp); if (unlikely(!__pyx_t_8)) __PYX_ERR(0, 27, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_8);
    __Pyx_DECREF(__pyx_t_7); __pyx_t_7 = 0;
    __pyx_t_7 = PyFloat_FromDouble((-pow(__pyx_v_x, 2.0))); if (unlikely(!__pyx_t_7)) __PYX_ERR(0, 27, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_7);
    __pyx_t_9 = NULL;
    if (CYTHON_UNPACK_METHODS && unlikely(PyMethod_Check(__pyx_t_8))) {
      __pyx_t_9 = PyMethod_GET_SELF(__pyx_t_8);
      if (likely(__pyx_t_9)) {
        PyObject* function = PyMethod_GET_FUNCTION(__pyx_t_8);
        __Pyx_INCREF(__pyx_t_9);
        __Pyx_INCREF(function);
        __Pyx_DECREF_SET(__pyx_t_8, function);
      }
    }
    __pyx_t_6 = (__pyx_t_9) ? __Pyx_PyObject_Call2Args(__pyx_t_8, __pyx_t_9, __pyx_t_7) : __Pyx_PyObject_CallOneArg(__pyx_t_8, __pyx_t_7);
    __Pyx_XDECREF(__pyx_t_9); __pyx_t_9 = 0;
    __Pyx_DECREF(__pyx_t_7); __pyx_t_7 = 0;
    if (unlikely(!__pyx_t_6)) __PYX_ERR(0, 27, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_6);
    __Pyx_DECREF(__pyx_t_8); __pyx_t_8 = 0;
    __pyx_t_8 = PyNumber_InPlaceAdd(__pyx_t_5, __pyx_t_6); if (unlikely(!__pyx_t_8)) __PYX_ERR(0, 27, __pyx_L1_error)
    __Pyx_GOTREF(__pyx_t_8);
    __Pyx_DECREF(__pyx_t_5); __pyx_t_5 = 0;
    __Pyx_DECREF(__pyx_t_6); __pyx_t_6 = 0;
    __pyx_t_1 = __pyx_PyFloat_AsDouble(__pyx_t_8); if (unlikely((__pyx_t_1 == (double)-1) && PyErr_Occurred())) __PYX_ERR(0, 27, __pyx_L1_error)
    __Pyx_DECREF(__pyx_t_8); __pyx_t_8 = 0;
    __pyx_v_sum_res = __pyx_t_1;
  }

+28:     return h_hat*sum_res

  __Pyx_XDECREF(__pyx_r);
  __pyx_t_8 = PyFloat_FromDouble((__pyx_v_h_hat * __pyx_v_sum_res)); if (unlikely(!__pyx_t_8)) __PYX_ERR(0, 28, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_8);
  __pyx_r = __pyx_t_8;
  __pyx_t_8 = 0;
  goto __pyx_L0;

Mejoramos el tiempo si directamente utilizamos la función exp de la librería math de Cython, ver calling C functions.

Rcf_5_cython.pyx

%%file Rcf_5_cython.pyx
from libc.math cimport exp as c_exp

cdef double f(double x) nogil:
    return c_exp(-x**2)
    
def Rcf(double a, double b, unsigned int n):
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
            
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    cdef unsigned int i
    cdef double x, sum_res, h_hat
    h_hat = (b-a)/n
    sum_res = 0
    for i in range(n):
        x = a+(i+1/2)*h_hat
        sum_res += f(x)
    return h_hat*sum_res

Writing Rcf_5_cython.pyx

%%bash
$HOME/.local/bin/cython -3 --force --annotate Rcf_5_cython.pyx

La liga correcta del archivo Rcf_5_cython.c es Rcf_5_cython.c

display(HTML("Rcf_5_cython.html"))

Generated by Cython 0.29.22

Yellow lines hint at Python interaction.
Click on a line that starts with a "+" to see the C code that Cython generated for it.

Raw output: Rcf_5_cython.c

 01: from libc.math cimport exp as c_exp

 02: 

+03: cdef double f(double x) nogil:

static double __pyx_f_12Rcf_5_cython_f(double __pyx_v_x) {
  double __pyx_r;
/* … */
  /* function exit code */
  __pyx_L0:;
  return __pyx_r;
}

+04:     return c_exp(-x**2)

  __pyx_r = exp((-pow(__pyx_v_x, 2.0)));
  goto __pyx_L0;

 05: 

+06: def Rcf(double a, double b, unsigned int n):

/* Python wrapper */
static PyObject *__pyx_pw_12Rcf_5_cython_1Rcf(PyObject *__pyx_self, PyObject *__pyx_args, PyObject *__pyx_kwds); /*proto*/
static char __pyx_doc_12Rcf_5_cython_Rcf[] = "\n    Compute numerical approximation using rectangle or mid-point\n    method in an interval.\n    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for\n    i=0,1,...,n-1 and h_hat=(b-a)/n\n    Args:\n            \n        a (float): left point of interval.\n        \n        b (float): right point of interval.\n        \n        n (int): number of subintervals.\n        \n    Returns:\n    \n        sum_res (float): numerical approximation to integral\n            of f in the interval a,b\n    ";
static PyMethodDef __pyx_mdef_12Rcf_5_cython_1Rcf = {"Rcf", (PyCFunction)(void*)(PyCFunctionWithKeywords)__pyx_pw_12Rcf_5_cython_1Rcf, METH_VARARGS|METH_KEYWORDS, __pyx_doc_12Rcf_5_cython_Rcf};
static PyObject *__pyx_pw_12Rcf_5_cython_1Rcf(PyObject *__pyx_self, PyObject *__pyx_args, PyObject *__pyx_kwds) {
  double __pyx_v_a;
  double __pyx_v_b;
  unsigned int __pyx_v_n;
  PyObject *__pyx_r = 0;
  __Pyx_RefNannyDeclarations
  __Pyx_RefNannySetupContext("Rcf (wrapper)", 0);
  {
    static PyObject **__pyx_pyargnames[] = {&__pyx_n_s_a,&__pyx_n_s_b,&__pyx_n_s_n,0};
    PyObject* values[3] = {0,0,0};
    if (unlikely(__pyx_kwds)) {
      Py_ssize_t kw_args;
      const Py_ssize_t pos_args = PyTuple_GET_SIZE(__pyx_args);
      switch (pos_args) {
        case  3: values[2] = PyTuple_GET_ITEM(__pyx_args, 2);
        CYTHON_FALLTHROUGH;
        case  2: values[1] = PyTuple_GET_ITEM(__pyx_args, 1);
        CYTHON_FALLTHROUGH;
        case  1: values[0] = PyTuple_GET_ITEM(__pyx_args, 0);
        CYTHON_FALLTHROUGH;
        case  0: break;
        default: goto __pyx_L5_argtuple_error;
      }
      kw_args = PyDict_Size(__pyx_kwds);
      switch (pos_args) {
        case  0:
        if (likely((values[0] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_a)) != 0)) kw_args--;
        else goto __pyx_L5_argtuple_error;
        CYTHON_FALLTHROUGH;
        case  1:
        if (likely((values[1] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_b)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 3, 3, 1); __PYX_ERR(0, 6, __pyx_L3_error)
        }
        CYTHON_FALLTHROUGH;
        case  2:
        if (likely((values[2] = __Pyx_PyDict_GetItemStr(__pyx_kwds, __pyx_n_s_n)) != 0)) kw_args--;
        else {
          __Pyx_RaiseArgtupleInvalid("Rcf", 1, 3, 3, 2); __PYX_ERR(0, 6, __pyx_L3_error)
        }
      }
      if (unlikely(kw_args > 0)) {
        if (unlikely(__Pyx_ParseOptionalKeywords(__pyx_kwds, __pyx_pyargnames, 0, values, pos_args, "Rcf") < 0)) __PYX_ERR(0, 6, __pyx_L3_error)
      }
    } else if (PyTuple_GET_SIZE(__pyx_args) != 3) {
      goto __pyx_L5_argtuple_error;
    } else {
      values[0] = PyTuple_GET_ITEM(__pyx_args, 0);
      values[1] = PyTuple_GET_ITEM(__pyx_args, 1);
      values[2] = PyTuple_GET_ITEM(__pyx_args, 2);
    }
    __pyx_v_a = __pyx_PyFloat_AsDouble(values[0]); if (unlikely((__pyx_v_a == (double)-1) && PyErr_Occurred())) __PYX_ERR(0, 6, __pyx_L3_error)
    __pyx_v_b = __pyx_PyFloat_AsDouble(values[1]); if (unlikely((__pyx_v_b == (double)-1) && PyErr_Occurred())) __PYX_ERR(0, 6, __pyx_L3_error)
    __pyx_v_n = __Pyx_PyInt_As_unsigned_int(values[2]); if (unlikely((__pyx_v_n == (unsigned int)-1) && PyErr_Occurred())) __PYX_ERR(0, 6, __pyx_L3_error)
  }
  goto __pyx_L4_argument_unpacking_done;
  __pyx_L5_argtuple_error:;
  __Pyx_RaiseArgtupleInvalid("Rcf", 1, 3, 3, PyTuple_GET_SIZE(__pyx_args)); __PYX_ERR(0, 6, __pyx_L3_error)
  __pyx_L3_error:;
  __Pyx_AddTraceback("Rcf_5_cython.Rcf", __pyx_clineno, __pyx_lineno, __pyx_filename);
  __Pyx_RefNannyFinishContext();
  return NULL;
  __pyx_L4_argument_unpacking_done:;
  __pyx_r = __pyx_pf_12Rcf_5_cython_Rcf(__pyx_self, __pyx_v_a, __pyx_v_b, __pyx_v_n);
  int __pyx_lineno = 0;
  const char *__pyx_filename = NULL;
  int __pyx_clineno = 0;

  /* function exit code */
  __Pyx_RefNannyFinishContext();
  return __pyx_r;
}

static PyObject *__pyx_pf_12Rcf_5_cython_Rcf(CYTHON_UNUSED PyObject *__pyx_self, double __pyx_v_a, double __pyx_v_b, unsigned int __pyx_v_n) {
  unsigned int __pyx_v_i;
  double __pyx_v_x;
  double __pyx_v_sum_res;
  double __pyx_v_h_hat;
  PyObject *__pyx_r = NULL;
  __Pyx_RefNannyDeclarations
  __Pyx_RefNannySetupContext("Rcf", 0);
/* … */
  /* function exit code */
  __pyx_L1_error:;
  __Pyx_XDECREF(__pyx_t_5);
  __Pyx_AddTraceback("Rcf_5_cython.Rcf", __pyx_clineno, __pyx_lineno, __pyx_filename);
  __pyx_r = NULL;
  __pyx_L0:;
  __Pyx_XGIVEREF(__pyx_r);
  __Pyx_RefNannyFinishContext();
  return __pyx_r;
}
/* … */
  __pyx_tuple_ = PyTuple_Pack(7, __pyx_n_s_a, __pyx_n_s_b, __pyx_n_s_n, __pyx_n_s_i, __pyx_n_s_x, __pyx_n_s_sum_res, __pyx_n_s_h_hat); if (unlikely(!__pyx_tuple_)) __PYX_ERR(0, 6, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_tuple_);
  __Pyx_GIVEREF(__pyx_tuple_);
/* … */
  __pyx_t_1 = PyCFunction_NewEx(&__pyx_mdef_12Rcf_5_cython_1Rcf, NULL, __pyx_n_s_Rcf_5_cython); if (unlikely(!__pyx_t_1)) __PYX_ERR(0, 6, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_1);
  if (PyDict_SetItem(__pyx_d, __pyx_n_s_Rcf, __pyx_t_1) < 0) __PYX_ERR(0, 6, __pyx_L1_error)
  __Pyx_DECREF(__pyx_t_1); __pyx_t_1 = 0;

 07:     """

 08:     Compute numerical approximation using rectangle or mid-point

 09:     method in an interval.

 10:     Nodes are generated via formula: x_i = a+(i+1/2)h_hat for

 11:     i=0,1,...,n-1 and h_hat=(b-a)/n

 12:     Args:

 13:             

 14:         a (float): left point of interval.

 15:         

 16:         b (float): right point of interval.

 17:         

 18:         n (int): number of subintervals.

 19:         

 20:     Returns:

 21:     

 22:         sum_res (float): numerical approximation to integral

 23:             of f in the interval a,b

 24:     """

 25:     cdef unsigned int i

 26:     cdef double x, sum_res, h_hat

+27:     h_hat = (b-a)/n

  __pyx_t_1 = (__pyx_v_b - __pyx_v_a);
  if (unlikely(__pyx_v_n == 0)) {
    PyErr_SetString(PyExc_ZeroDivisionError, "float division");
    __PYX_ERR(0, 27, __pyx_L1_error)
  }
  __pyx_v_h_hat = (__pyx_t_1 / ((double)__pyx_v_n));

+28:     sum_res = 0

  __pyx_v_sum_res = 0.0;

+29:     for i in range(n):

  __pyx_t_2 = __pyx_v_n;
  __pyx_t_3 = __pyx_t_2;
  for (__pyx_t_4 = 0; __pyx_t_4 < __pyx_t_3; __pyx_t_4+=1) {
    __pyx_v_i = __pyx_t_4;

+30:         x = a+(i+1/2)*h_hat

    __pyx_v_x = (__pyx_v_a + ((__pyx_v_i + (1.0 / 2.0)) * __pyx_v_h_hat));

+31:         sum_res += f(x)

    __pyx_v_sum_res = (__pyx_v_sum_res + __pyx_f_12Rcf_5_cython_f(__pyx_v_x));
  }

+32:     return h_hat*sum_res

  __Pyx_XDECREF(__pyx_r);
  __pyx_t_5 = PyFloat_FromDouble((__pyx_v_h_hat * __pyx_v_sum_res)); if (unlikely(!__pyx_t_5)) __PYX_ERR(0, 32, __pyx_L1_error)
  __Pyx_GOTREF(__pyx_t_5);
  __pyx_r = __pyx_t_5;
  __pyx_t_5 = 0;
  goto __pyx_L0;

Comentario

Un tradeoff en la optimización de código se realiza entre flexibilidad, legibilidad y una ejecución rápida del código.

%%file setup_2.py
from distutils.core import setup
from Cython.Build import cythonize

setup(ext_modules = cythonize("Rcf_2_cython.pyx", 
                              compiler_directives={'language_level' : 3})
     )

Writing setup_2.py

Compilar desde la línea de comandos:

%%bash
python3 setup_2.py build_ext --inplace

running build_ext
building 'Rcf_2_cython' extension
x86_64-linux-gnu-gcc -pthread -Wno-unused-result -Wsign-compare -DNDEBUG -g -fwrapv -O2 -Wall -g -fstack-protector-strong -Wformat -Werror=format-security -g -fwrapv -O2 -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -I/usr/include/python3.8 -c Rcf_2_cython.c -o build/temp.linux-x86_64-3.8/Rcf_2_cython.o
x86_64-linux-gnu-gcc -pthread -shared -Wl,-O1 -Wl,-Bsymbolic-functions -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fwrapv -O2 -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fwrapv -O2 -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 build/temp.linux-x86_64-3.8/Rcf_2_cython.o -o /home/ubuntu/analisis-numerico-computo-cientifico/libro_optimizacion/temas/V.optimizacion_de_codigo/5.3/Rcf_2_cython.cpython-38-x86_64-linux-gnu.so

%%file setup_3.py
from distutils.core import setup
from Cython.Build import cythonize

setup(ext_modules = cythonize("Rcf_3_cython.pyx", 
                              compiler_directives={'language_level' : 3})
     )

Writing setup_3.py

Compilar desde la línea de comandos:

%%bash
python3 setup_3.py build_ext --inplace

running build_ext
building 'Rcf_3_cython' extension
x86_64-linux-gnu-gcc -pthread -Wno-unused-result -Wsign-compare -DNDEBUG -g -fwrapv -O2 -Wall -g -fstack-protector-strong -Wformat -Werror=format-security -g -fwrapv -O2 -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -I/usr/include/python3.8 -c Rcf_3_cython.c -o build/temp.linux-x86_64-3.8/Rcf_3_cython.o
x86_64-linux-gnu-gcc -pthread -shared -Wl,-O1 -Wl,-Bsymbolic-functions -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fwrapv -O2 -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fwrapv -O2 -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 build/temp.linux-x86_64-3.8/Rcf_3_cython.o -o /home/ubuntu/analisis-numerico-computo-cientifico/libro_optimizacion/temas/V.optimizacion_de_codigo/5.3/Rcf_3_cython.cpython-38-x86_64-linux-gnu.so

%%file setup_4.py
from distutils.core import setup
from Cython.Build import cythonize

setup(ext_modules = cythonize("Rcf_4_cython.pyx", 
                              compiler_directives={'language_level' : 3})
     )

Writing setup_4.py

Compilar desde la línea de comandos:

%%bash
python3 setup_4.py build_ext --inplace

running build_ext
building 'Rcf_4_cython' extension
x86_64-linux-gnu-gcc -pthread -Wno-unused-result -Wsign-compare -DNDEBUG -g -fwrapv -O2 -Wall -g -fstack-protector-strong -Wformat -Werror=format-security -g -fwrapv -O2 -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -I/usr/include/python3.8 -c Rcf_4_cython.c -o build/temp.linux-x86_64-3.8/Rcf_4_cython.o
x86_64-linux-gnu-gcc -pthread -shared -Wl,-O1 -Wl,-Bsymbolic-functions -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fwrapv -O2 -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fwrapv -O2 -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 build/temp.linux-x86_64-3.8/Rcf_4_cython.o -o /home/ubuntu/analisis-numerico-computo-cientifico/libro_optimizacion/temas/V.optimizacion_de_codigo/5.3/Rcf_4_cython.cpython-38-x86_64-linux-gnu.so

%%file setup_5.py
from distutils.core import setup
from Cython.Build import cythonize

setup(ext_modules = cythonize("Rcf_5_cython.pyx", 
                              compiler_directives={'language_level' : 3})
     )

Writing setup_5.py

Compilar desde la línea de comandos:

%%bash
python3 setup_5.py build_ext --inplace

running build_ext
building 'Rcf_5_cython' extension
x86_64-linux-gnu-gcc -pthread -Wno-unused-result -Wsign-compare -DNDEBUG -g -fwrapv -O2 -Wall -g -fstack-protector-strong -Wformat -Werror=format-security -g -fwrapv -O2 -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -I/usr/include/python3.8 -c Rcf_5_cython.c -o build/temp.linux-x86_64-3.8/Rcf_5_cython.o
x86_64-linux-gnu-gcc -pthread -shared -Wl,-O1 -Wl,-Bsymbolic-functions -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fwrapv -O2 -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fwrapv -O2 -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 build/temp.linux-x86_64-3.8/Rcf_5_cython.o -o /home/ubuntu/analisis-numerico-computo-cientifico/libro_optimizacion/temas/V.optimizacion_de_codigo/5.3/Rcf_5_cython.cpython-38-x86_64-linux-gnu.so

Importar módulos compilados:

import Rcf_2_cython, Rcf_3_cython, Rcf_4_cython, Rcf_5_cython

start_time = time.time()
res_2 = Rcf_2_cython.Rcf(f, a, b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf_2 tomó",secs,"segundos" )

Rcf_2 tomó 3.3402740955352783 segundos

Verificamos que después de la optimización de código continuamos resolviendo correctamente el problema:

print(res_2 == approx(obj))

True

start_time = time.time()
res_3 = Rcf_3_cython.Rcf(f, a, b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf_3 tomó",secs,"segundos" )

Rcf_3 tomó 2.496501922607422 segundos

print(res_3 == approx(obj))

True

start_time = time.time()
res_4 = Rcf_4_cython.Rcf(a, b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf_4 tomó",secs,"segundos" )

Rcf_4 tomó 0.7289412021636963 segundos

print(res_4 == approx(obj))

True

start_time = time.time()
res_5 = Rcf_5_cython.Rcf(a, b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf_5 tomó",secs,"segundos" )

Rcf_5 tomó 0.10629606246948242 segundos

Verificamos que después de la optimización de código continuamos resolviendo correctamente el problema:

print(res_5 == approx(obj))

True

Ejemplo de implementación con NumPy

Comparamos con una implementación usando NumPy y vectorización:

import numpy as np

f_np = lambda x: np.exp(-x**2)

Rcf_numpy

def Rcf_numpy(f,a,b,n):
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
    
        f (float): function expression of integrand.
        
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    h_hat = (b-a)/n
    aux_vec = np.linspace(a, b, n+1)
    nodes = (aux_vec[:-1]+aux_vec[1:])/2
    return h_hat*np.sum(f(nodes))

start_time = time.time()
res_numpy = Rcf_numpy(f_np, a, b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf_numpy tomó",secs,"segundos" )

Rcf_numpy tomó 0.273637056350708 segundos

print(res_numpy == approx(obj))

True

Comentarios

• La implementación con NumPy resulta ser la segunda más rápida principalmente por el uso de bloques contiguos de memoria para almacenar los valores y la vectorización. La implementación anterior, sin embargo, requiere un conocimiento de las funciones de tal paquete. Para este ejemplo utilizamos linspace y la funcionalidad de realizar operaciones de forma vectorizada para la creación de los nodos y evaluación de la función. Una situación que podría darse es que para un problema no podamos utilizar alguna función de NumPy o bien no tengamos el ingenio para pensar cómo realizar una operación de forma vectorizada. En este caso Cython puede ser una opción a utilizar.

• En Cython se tienen las memoryviews para acceso de bajo nivel a la memoria similar a la que proveen los arrays de NumPy en el caso de requerirse arrays en una forma más general que no sólo sean de NumPy (por ejemplo de C o de Cython, ver Cython arrays).

Observación

Compárese la implementación vía NumPy con el uso de listas para los nodos. Recuérdese que las listas de Python alojan locaciones donde se pueden encontrar los valores y no los valores en sí. Los arrays de NumPy almacenan tipos de valores primitivos. Las listas tienen data fragmentation que causan memory fragmentation y por tanto un mayor impacto del Von Neumann bottleneck. Además el almacenamiento de tipo de objetos de alto nivel en las listas causa overhead en lugar de almacenamiento de tipo de valores primitivos en un array de NumPy.

Cython y OpenMP

OpenMP es una extensión al lenguaje C y es una API para cómputo en paralelo en un sistema de memoria compartida, aka, shared memory parallel programming con CPUs. Se revisará con mayor profundidad en la nota de cómputo en paralelo.

Ver global interpreter lock (GIL), global interpreter lock

En Cython, OpenMP se utiliza mediante prange (parallel range). Además debe deshabilitarse el GIL.

Observación

Al deshabilitar el GIL en una sección de código se debe operar con tipos primitivos. En tal sección no se debe operar con objetos Python (por ejemplo listas).

Rcf_5_cython_openmp

%%file Rcf_5_cython_openmp.pyx
from cython.parallel import prange
from libc.math cimport exp as c_exp

cdef double f(double x) nogil:
    return c_exp(-x**2)

def Rcf(double a, double b, unsigned int n):
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
            
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    cdef int i
    cdef double x, sum_res, h_hat
    h_hat = (b-a)/n
    sum_res = 0
    for i in prange(n, schedule="guided", nogil=True):
        x = a+(i+1/2)*h_hat
        sum_res += f(x)
    return h_hat*sum_res

Writing Rcf_5_cython_openmp.pyx

Comentario

Con prange puede elegirse diferente scheduling. Si schedule recibe el valor static el trabajo a realizar se reparte equitativamente entre los cores y si algunos threads terminan antes permanecerán sin realizar trabajo, aka idle. Con dynamic y guided se reparte de manera dinámica at runtime que es útil si la cantidad de trabajo es variable y si threads terminan antes pueden recibir trabajo a realizar.

%%bash
$HOME/.local/bin/cython -3 --force Rcf_5_cython_openmp.pyx

En el archivo setup.py se coloca la directiva -fopenmp.

Ver Rcf_5_cython_openmp.c para la implementación en C de la función Rcf_5_cython_openmp.Rcf.

%%file setup_5_openmp.py
from setuptools import Extension, setup
from Cython.Build import cythonize

ext_modules = [Extension("Rcf_5_cython_openmp",
                         ["Rcf_5_cython_openmp.pyx"], 
                         extra_compile_args=["-fopenmp"],
                         extra_link_args=["-fopenmp"],
                        )
              ]

setup(ext_modules = cythonize(ext_modules))

Writing setup_5_openmp.py

Compilar desde la línea de comandos:

%%bash
python3 setup_5_openmp.py build_ext --inplace

running build_ext
building 'Rcf_5_cython_openmp' extension
x86_64-linux-gnu-gcc -pthread -Wno-unused-result -Wsign-compare -DNDEBUG -g -fwrapv -O2 -Wall -g -fstack-protector-strong -Wformat -Werror=format-security -g -fwrapv -O2 -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -I/usr/include/python3.8 -c Rcf_5_cython_openmp.c -o build/temp.linux-x86_64-3.8/Rcf_5_cython_openmp.o -fopenmp
creating build/lib.linux-x86_64-3.8
x86_64-linux-gnu-gcc -pthread -shared -Wl,-O1 -Wl,-Bsymbolic-functions -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fwrapv -O2 -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fwrapv -O2 -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 build/temp.linux-x86_64-3.8/Rcf_5_cython_openmp.o -o build/lib.linux-x86_64-3.8/Rcf_5_cython_openmp.cpython-38-x86_64-linux-gnu.so -fopenmp
copying build/lib.linux-x86_64-3.8/Rcf_5_cython_openmp.cpython-38-x86_64-linux-gnu.so -> 

import Rcf_5_cython_openmp

start_time = time.time()
res_5_openmp = Rcf_5_cython_openmp.Rcf(a, b, n)
end_time = time.time()

secs = end_time-start_time
print("Rcf_5_openmp tomó",secs,"segundos" )

Rcf_5_openmp tomó 0.017746686935424805 segundos

Verificamos que después de la optimización de código continuamos resolviendo correctamente el problema:

print(res_5_openmp == approx(obj))

True

Ejercicio

Implementar la regla de Simpson compuesta con NumPy, Cython y Cython + OpenMP en una máquina de AWS con las mismas características que la que se presenta en esta nota y medir tiempo de ejecución.

Numba

• Utiliza compilación JIT at runtime mediante el compilador llvmlite.

• Puede utilizarse para funciones built in de Python o de NumPy.

• Tiene soporte para cómputo en paralelo en CPU/GPU.

• Utiliza CFFI y ctypes para llamar a funciones de C.

• Ver numba architecture para una explicación detallada de su funcionamiento.

Se utiliza un decorator para anotar cuál función se desea compilar.

Ejemplo de uso con Numba

from numba import jit

En glossary: nopython se da la definición de nopython mode en Numba. Ahí se indica que se genera código que no usa Python C API y requiere que los tipos de valores nativos de Python puedan ser inferidos.

Puede usarse el decorator njit que es un alias para @jit(nopython=True).

Rcf_numba

@jit(nopython=True)
def Rcf_numba(a,b,n):
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
            
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    h_hat = (b-a)/n
    sum_res = 0
    for i in range(n):
        x = a+(i+1/2)*h_hat
        sum_res += np.exp(-x**2)
    return h_hat*sum_res

start_time = time.time()
res_numba = Rcf_numba(a,b,n)
end_time = time.time()

Se mide dos veces el tiempo de ejecución para no incluir el tiempo de compilación. Ver 5minguide.

secs = end_time-start_time
print("Rcf_numba con compilación tomó", secs, "segundos" )

Rcf_numba con compilación tomó 0.5527660846710205 segundos

start_time = time.time()
res_numba = Rcf_numba(a,b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf_numba tomó", secs, "segundos" )

Rcf_numba tomó 0.22369146347045898 segundos

Verificamos que después de la optimización de código continuamos resolviendo correctamente el problema:

print(res_numba == approx(obj))

True

Con la función inspect_types nos ayuda para revisar si pudo inferirse información de los tipos de valores a partir del código escrito.

print(Rcf_numba.inspect_types())

Rcf_numba (int64, int64, int64)
--------------------------------------------------------------------------------
# File: <ipython-input-71-541f7545b9ed>
# --- LINE 1 --- 

@jit(nopython=True)

# --- LINE 2 --- 

def Rcf_numba(a,b,n):

    # --- LINE 3 --- 

    """

    # --- LINE 4 --- 

    Compute numerical approximation using rectangle or mid-point

    # --- LINE 5 --- 

    method in an interval.

    # --- LINE 6 --- 

    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for

    # --- LINE 7 --- 

    i=0,1,...,n-1 and h_hat=(b-a)/n

    # --- LINE 8 --- 

    Args:

# --- LINE 9 --- 



        # --- LINE 10 --- 

        a (float): left point of interval.

# --- LINE 11 --- 



        # --- LINE 12 --- 

        b (float): right point of interval.

# --- LINE 13 --- 



        # --- LINE 14 --- 

        n (int): number of subintervals.

# --- LINE 15 --- 



    # --- LINE 16 --- 

    Returns:

# --- LINE 17 --- 



        # --- LINE 18 --- 

        sum_res (float): numerical approximation to integral

            # --- LINE 19 --- 

            of f in the interval a,b

    # --- LINE 20 --- 

    """

    # --- LINE 21 --- 
    # label 0
    #   a = arg(0, name=a)  :: int64
    #   b = arg(1, name=b)  :: int64
    #   n = arg(2, name=n)  :: int64
    #   $6binary_subtract.2 = b - a  :: int64
    #   del b
    #   h_hat = $6binary_subtract.2 / n  :: float64
    #   del $6binary_subtract.2

    h_hat = (b-a)/n

    # --- LINE 22 --- 
    #   sum_res = const(int, 0)  :: Literal[int](0)

    sum_res = 0

    # --- LINE 23 --- 
    #   $18load_global.6 = global(range: <class 'range'>)  :: Function(<class 'range'>)
    #   $22call_function.8 = call $18load_global.6(n, func=$18load_global.6, args=[Var(n, <ipython-input-71-541f7545b9ed>:21)], kws=(), vararg=None)  :: (int64,) -> range_state_int64
    #   del n
    #   del $18load_global.6
    #   $24get_iter.9 = getiter(value=$22call_function.8)  :: range_iter_int64
    #   del $22call_function.8
    #   $phi26.0 = $24get_iter.9  :: range_iter_int64
    #   del $24get_iter.9
    #   jump 26
    # label 26
    #   sum_res.2 = phi(incoming_values=[Var(sum_res, <ipython-input-71-541f7545b9ed>:22), Var(sum_res.1, <ipython-input-71-541f7545b9ed>:25)], incoming_blocks=[0, 28])  :: float64
    #   del sum_res.1
    #   $26for_iter.1 = iternext(value=$phi26.0)  :: pair<int64, bool>
    #   $26for_iter.2 = pair_first(value=$26for_iter.1)  :: int64
    #   $26for_iter.3 = pair_second(value=$26for_iter.1)  :: bool
    #   del $26for_iter.1
    #   $phi28.1 = $26for_iter.2  :: int64
    #   del $26for_iter.2
    #   branch $26for_iter.3, 28, 68
    # label 28
    #   del $26for_iter.3
    #   i = $phi28.1  :: int64
    #   del $phi28.1

    for i in range(n):

        # --- LINE 24 --- 
        #   $const34.4 = const(float, 0.5)  :: float64
        #   $36binary_add.5 = i + $const34.4  :: float64
        #   del i
        #   del $const34.4
        #   $40binary_multiply.7 = $36binary_add.5 * h_hat  :: float64
        #   del $36binary_add.5
        #   x = a + $40binary_multiply.7  :: float64
        #   del $40binary_multiply.7

        x = a+(i+1/2)*h_hat

        # --- LINE 25 --- 
        #   $48load_global.10 = global(np: <module 'numpy' from '/home/ubuntu/.local/lib/python3.8/site-packages/numpy/__init__.py'>)  :: Module(<module 'numpy' from '/home/ubuntu/.local/lib/python3.8/site-packages/numpy/__init__.py'>)
        #   $50load_method.11 = getattr(value=$48load_global.10, attr=exp)  :: Function(<ufunc 'exp'>)
        #   del $48load_global.10
        #   $const54.13 = const(int, 2)  :: Literal[int](2)
        #   $56binary_power.14 = x ** $const54.13  :: float64
        #   del x
        #   del $const54.13
        #   $58unary_negative.15 = unary(fn=<built-in function neg>, value=$56binary_power.14)  :: float64
        #   del $56binary_power.14
        #   $60call_method.16 = call $50load_method.11($58unary_negative.15, func=$50load_method.11, args=[Var($58unary_negative.15, <ipython-input-71-541f7545b9ed>:25)], kws=(), vararg=None)  :: (float64,) -> float64
        #   del $58unary_negative.15
        #   del $50load_method.11
        #   $62inplace_add.17 = inplace_binop(fn=<built-in function iadd>, immutable_fn=<built-in function add>, lhs=sum_res.2, rhs=$60call_method.16, static_lhs=Undefined, static_rhs=Undefined)  :: float64
        #   del sum_res.2
        #   del $60call_method.16
        #   sum_res.1 = $62inplace_add.17  :: float64
        #   del $62inplace_add.17
        #   jump 26

        sum_res += np.exp(-x**2)

    # --- LINE 26 --- 
    # label 68
    #   del sum_res
    #   del a
    #   del $phi28.1
    #   del $phi26.0
    #   del $26for_iter.3
    #   $72binary_multiply.2 = h_hat * sum_res.2  :: float64
    #   del sum_res.2
    #   del h_hat
    #   $74return_value.3 = cast(value=$72binary_multiply.2)  :: float64
    #   del $72binary_multiply.2
    #   return $74return_value.3

    return h_hat*sum_res


================================================================================
None

Ejemplo de uso de Numba con cómputo en paralelo

Ver numba: parallel, numba: threading layer

from numba import prange

Rcf_numba_parallel

@jit(nopython=True, parallel=True)
def Rcf_numba_parallel(a,b,n):
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
            
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    h_hat = (b-a)/n
    sum_res = 0
    for i in prange(n):
        x = a+(i+1/2)*h_hat
        sum_res += np.exp(-x**2)
    return h_hat*sum_res

start_time = time.time()
res_numba_parallel = Rcf_numba_parallel(a,b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf_numba_parallel con compilación tomó", secs, "segundos" )

Rcf_numba_parallel con compilación tomó 1.074690580368042 segundos

start_time = time.time()
res_numba_parallel = Rcf_numba_parallel(a,b,n)
end_time = time.time()

Ver parallel-diagnostics para información relacionada con la ejecución en paralelo. Por ejemplo ejecutar Rcf_numba_parallel.parallel_diagnostics(level=4).

secs = end_time-start_time
print("Rcf_numba_parallel tomó", secs, "segundos" )

Rcf_numba_parallel tomó 0.011192798614501953 segundos

Verificamos que después de la optimización de código continuamos resolviendo correctamente el problema:

print(res_numba_parallel == approx(obj))

True

Ejemplo Numpy y Numba

En el siguiente ejemplo se utiliza la función linspace para auxiliar en la creación de los nodos y obsérvese que Numba sin problema trabaja los ciclos for (en el caso por ejemplo que no hubiéramos podido vectorizar la operación de creación de nodos).

@jit(nopython=True)
def Rcf_numpy_numba(a,b,n):
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
            
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    h_hat = (b-a)/n
    aux_vec = np.linspace(a, b, n+1)
    sum_res = 0
    for i in range(n-1):
        x = (aux_vec[i]+aux_vec[i+1])/2
        sum_res += np.exp(-x**2)
    return h_hat*sum_res

start_time = time.time()
res_numpy_numba = Rcf_numpy_numba(a, b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf_numpy_numba con compilación tomó",secs,"segundos" )

Rcf_numpy_numba con compilación tomó 0.5971698760986328 segundos

start_time = time.time()
res_numpy_numba = Rcf_numpy_numba(a, b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf_numpy_numba tomó",secs,"segundos" )

Rcf_numpy_numba tomó 0.1863393783569336 segundos

print(res_numpy_numba == approx(obj))

True

@jit(nopython=True)
def Rcf_numpy_numba_2(a,b,n):
    """
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
            
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    """
    h_hat = (b-a)/n
    aux_vec = np.linspace(a, b, n+1)
    nodes = (aux_vec[:-1]+aux_vec[1:])/2
    return h_hat*np.sum(np.exp(-nodes**2))

start_time = time.time()
res_numpy_numba_2 = Rcf_numpy_numba_2(a, b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf_numpy_numba_2 con compilación tomó",secs,"segundos" )

Rcf_numpy_numba_2 con compilación tomó 0.8459124565124512 segundos

start_time = time.time()
res_numpy_numba_2 = Rcf_numpy_numba_2(a, b,n)
end_time = time.time()

secs = end_time-start_time
print("Rcf_numpy_numba_2 tomó",secs,"segundos" )

Rcf_numpy_numba_2 tomó 0.26958131790161133 segundos

print(res_numpy_numba_2 == approx(obj))

True

Observación

Obsérvese que no se mejora el tiempo de ejecución utilizando vectorización y linspace que usando un ciclo for en la implementación anterior Rcf_numpy_numba. De hecho en Rcf_numpy_numba_2 tiene un tiempo de ejecución igual que Rcf_numpy.

Ejercicio

Implementar la regla de Simpson compuesta con Numba, Numpy y Numba, Numba con cómputo en paralelo en una máquina de AWS con las mismas características que la que se presenta en esta nota y medir tiempo de ejecución.

Rcpp

Rcpp permite integrar C++ y R de forma sencilla mediante su API.

¿Por qué usar Rcpp?

Con Rcpp nos da la posibilidad de obtener eficiencia en ejecución de un código con C++ conservando la flexibilidad de trabajar con R. C o C++ aunque requieren más líneas de código, son órdenes de magnitud más rápidos que R. Sacrificamos las ventajas que tiene R como facilidad de escribir códigos por velocidad en ejecución.

¿Cuando podríamos usar Rcpp?

• En loops que no pueden vectorizarse de forma sencilla. Si tenemos loops en los que una iteración depende de la anterior.

• Si hay que llamar una función millones de veces.

¿Por qué no usamos C?

Sí es posible llamar funciones de C desde R pero resulta en más trabajo por parte de nosotros. Por ejemplo, de acuerdo a H. Wickham:

“…R’s C API. Unfortunately this API is not well documented. I’d recommend starting with my notes at R’s C interface. After that, read “The R API” in “Writing R Extensions”. A number of exported functions are not documented, so you’ll also need to read the R source code to figure out the details.”

Y como primer acercamiento a la compilación de código desde R es preferible seguir las recomendaciones de H. Wickham en utilizar la API de Rcpp.

Ejemplo con Rcpp

En la siguiente implementación se utiliza vapply que es más rápida que sapply pues se especifica con anterioridad el tipo de valor que devuelve.

Rcf <- function(f,a,b,n){
    '
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
    
        f (float): function expression of integrand.
        
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    '
    h_hat <- (b-a)/n
    sum_res <- 0
    x <- vapply(0:(n-1),function(j)a+(j+1/2)*h_hat,numeric(1))
    for(j in 1:n){
        sum_res <- sum_res+f(x[j])
    }
    h_hat*sum_res
}

a <- 0
b <- 1
f <- function(x)exp(-x^2)
n <- 10**7

system.time(res <- Rcf(f,a,b,n))

   user  system elapsed 
 13.988   0.111  14.100 

err_relativo <- function(aprox,obj)abs(aprox-obj)/abs(obj)

En la documentación de integrate se menciona que se utilice Vectorize.

obj <- integrate(Vectorize(f),0,1) 

print(err_relativo(res,obj$value))

[1] 4.99495e-14

Rcf_2 <- function(f,a,b,n){
    '
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
    
        f (float): function expression of integrand.
        
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    '
    h_hat <- (b-a)/n
    x <- vapply(0:(n-1),function(j)a+(j+1/2)*h_hat,numeric(1))
    h_hat*sum(f(x))
}

system.time(res_2 <- Rcf_2(f,a,b,n))

   user  system elapsed 
 10.658   0.133  10.792 

print(err_relativo(res_2,obj$value))

[1] 2.973185e-16

library(Rcpp)

En Rcpp se tiene la función cppFunction que recibe código escrito en C++ para definir una función que puede ser utilizada desde R.

Primero reescribamos la implementación en la que no utilicemos vapply.

Rcf_3 <- function(f,a,b,n){
    '
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
    
        f (float): function expression of integrand.
        
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    '
    h_hat <- (b-a)/n
    sum_res <- 0
    for(i in 0:(n-1)){
        x <- a+(i+1/2)*h_hat
        sum_res <- sum_res+f(x)
    }
    h_hat*sum_res
}

system.time(res_3 <- Rcf_3(f,a,b,n))

   user  system elapsed 
  5.768   0.000   5.769 

print(err_relativo(res_3,obj$value))

[1] 4.99495e-14

Rcf_Rcpp

Escribimos source code en C++ que será el primer parámetro que recibirá cppFunction.

f_str <- 'double Rcf_Rcpp(double a, double b, int n){
             double h_hat;
             double sum_res=0;
             int i;
             double x;
             h_hat=(b-a)/n;
             for(i=0;i<=n-1;i++){
                    x = a+(i+1/2.0)*h_hat;
                    sum_res += exp(-pow(x,2));
             }
             return h_hat*sum_res;
         }'

cppFunction(f_str)

Si queremos obtener más información de la ejecución de la línea anterior podemos usar lo siguiente.

Se utiliza rebuild=TRUE para que se vuelva a compilar, ligar con la librería en C++ y más operaciones de cppFunction.

cppFunction(f_str, verbose=TRUE, rebuild=TRUE) 

Generated code for function definition: 
--------------------------------------------------------

#include <Rcpp.h>

using namespace Rcpp;

// [[Rcpp::export]]
double Rcf_Rcpp(double a, double b, int n){
             double h_hat;
             double sum_res=0;
             int i;
             double x;
             h_hat=(b-a)/n;
             for(i=0;i<=n-1;i++){
                    x = a+(i+1/2.0)*h_hat;
                    sum_res += exp(-pow(x,2));
             }
             return h_hat*sum_res;
         }

Generated extern "C" functions 
--------------------------------------------------------


#include <Rcpp.h>
// Rcf_Rcpp
double Rcf_Rcpp(double a, double b, int n);
RcppExport SEXP sourceCpp_4_Rcf_Rcpp(SEXP aSEXP, SEXP bSEXP, SEXP nSEXP) {
BEGIN_RCPP
    Rcpp::RObject rcpp_result_gen;
    Rcpp::RNGScope rcpp_rngScope_gen;
    Rcpp::traits::input_parameter< double >::type a(aSEXP);
    Rcpp::traits::input_parameter< double >::type b(bSEXP);
    Rcpp::traits::input_parameter< int >::type n(nSEXP);
    rcpp_result_gen = Rcpp::wrap(Rcf_Rcpp(a, b, n));
    return rcpp_result_gen;
END_RCPP
}

Generated R functions 
-------------------------------------------------------

`.sourceCpp_4_DLLInfo` <- dyn.load('/tmp/RtmpTz18Yr/sourceCpp-x86_64-pc-linux-gnu-1.0.6/sourcecpp_3684ee9b3bc/sourceCpp_6.so')

Rcf_Rcpp <- Rcpp:::sourceCppFunction(function(a, b, n) {}, FALSE, `.sourceCpp_4_DLLInfo`, 'sourceCpp_4_Rcf_Rcpp')

rm(`.sourceCpp_4_DLLInfo`)

Building shared library
--------------------------------------------------------

DIR: /tmp/RtmpTz18Yr/sourceCpp-x86_64-pc-linux-gnu-1.0.6/sourcecpp_3684ee9b3bc

/usr/lib/R/bin/R CMD SHLIB --preclean -o 'sourceCpp_6.so' 'file3684a4b1d19.cpp' 

Comentarios

• Al ejecutar la línea de cppFunction, Rcpp compilará el código de C++ y construirá una función de R que se conecta con la función compilada de C++.

• Si se lee la salida de la ejecución con verbose=TRUE se utiliza un tipo de valor SEXP. De acuerdo a H. Wickham:

…functions that talk to R must use the SEXP type for both inputs and outputs. SEXP, short for S expression, is the C struct used to represent every type of object in R. A C function typically starts by converting SEXPs to atomic C objects, and ends by converting C objects back to a SEXP. (The R API is designed so that these conversions often don’t require copying.)

• La función Rcpp::wrap convierte objetos de C++ a objetos de R y Rcpp:as viceversa.

system.time(res_4 <- Rcf_Rcpp(a,b,n))

   user  system elapsed 
  0.106   0.000   0.106 

print(err_relativo(res_4,obj$value))

[1] 4.99495e-14

Otras funcionalidades de Rcpp

NumericVector

En Rcpp se definen clases para relacionar tipos de valores de R con tipo de valores de C++ para el manejo de vectores. Entre éstas se encuentran NumericVector, IntegerVector, CharacterVector y LogicalVector que se relacionan con vectores tipo numeric, integer, character y logical respectivamente.

Por ejemplo, para el caso de NumericVector se tiene el siguiente ejemplo.

f_str <- 'NumericVector my_f(NumericVector x){
          return exp(log(x));
         }'

cppFunction(f_str)

print(my_f(seq(0,1,by=.1)))

 [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

Ejemplo con NumericVector

Para mostrar otro ejemplo en el caso de la regla de integración del rectángulo considérese la siguiente implementación.

Rcf_implementation_example <- function(f,a,b,n){
    '
    Compute numerical approximation using rectangle or mid-point
    method in an interval.
    
    Nodes are generated via formula: x_i = a+(i+1/2)h_hat for
    i=0,1,...,n-1 and h_hat=(b-a)/n
    Args:
    
        f (float): function expression of integrand.
        
        a (float): left point of interval.
        
        b (float): right point of interval.
        
        n (int): number of subintervals.
        
    Returns:
    
        sum_res (float): numerical approximation to integral
            of f in the interval a,b
    '
    h_hat <- (b-a)/n
    fx <- f(vapply(0:(n-1),function(j)a+(j+1/2)*h_hat,numeric(1)))
    h_hat*sum(fx)
}

res_numeric_vector <- Rcf_implementation_example(f,a,b,n)

print(err_relativo(res_numeric_vector,obj$value))

[1] 2.973185e-16

Utilicemos Rcpp para definir una función que recibe un NumericVector para realizar la suma.

El método .size() regresa un integer.

f_str<-'double Rcf_numeric_vector(NumericVector f_x,double h_hat){
             double sum_res=0;
             int i;
             int n = f_x.size();
             for(i=0;i<=n-1;i++){
                    sum_res+=f_x[i];
             }
             return h_hat*sum_res;
        }'

h_hat <- (b-a)/n

fx <- f(vapply(0:(n-1),function(j)a+(j+1/2)*h_hat,numeric(1)))

print(tail(fx))

[1] 0.3678798 0.3678798 0.3678797 0.3678796 0.3678796 0.3678795

cppFunction(f_str,rebuild=TRUE)

res_numeric_vector <- Rcf_numeric_vector(fx,h_hat)

print(err_relativo(res_numeric_vector,obj$value))

[1] 4.99495e-14

Otro ejemplo en el que se devuelve un vector tipo NumericVector para crear los nodos.

f_str <- 'NumericVector Rcf_nodes(double a, double b, int n){
          double h_hat=(b-a)/n;
          int i;
          NumericVector x(n);
          for(i=0;i<n;i++)
              x[i]=a+(i+1/2.0)*h_hat;
          return x;
         }'

cppFunction(f_str,rebuild=TRUE)

print(Rcf_nodes(0,1,2))

[1] 0.25 0.75

Ejemplo de llamado a función definida en ambiente global con Rcpp

También en Rcpp es posible llamar funciones definidas en el ambiente global, por ejemplo.

RObject es una clase de C++ para definir un objeto de R.

f_str <- 'RObject fun(double x){
          Environment env = Environment::global_env();
          Function f=env["f"];
          return f(x);
          }'

cppFunction(f_str,rebuild=TRUE)

fun(1)

0.367879441171442

f(1)

0.367879441171442

print(fun)

function (x) 
.Call(<pointer: 0x7fba201b25f0>, x)

Comentario

.Call es una función base para llamar funciones de C desde R:

There are two ways to call C functions from R: .C() and .Call(). .C() is a quick and dirty way to call an C function that doesn’t know anything about R because .C() automatically converts between R vectors and the corresponding C types. .Call() is more flexible, but more work: your C function needs to use the R API to convert its inputs to standard C data types.

H. Wickham.

print(f)

function(x)exp(-x^2)
<bytecode: 0x55669726fec8>

Ejercicio

Revisar rcpp-sugar, Rcpp syntactic sugar y proponer programas que utilicen sugar.

Ejercicio

Implementar la regla de Simpson compuesta con Rcpp en una máquina de AWS con las mismas características que la que se presenta en esta nota y medir tiempo de ejecución.

Comentario

También existe el paquete RcppParallel para cómputo en paralelo con la funcionalidad de Rcpp.

Tabla resúmen con códigos que reportaron los mejores tiempos

En la siguiente tabla se presentan ligas hacia las implementaciones de la regla del rectángulo compuesta en diferentes lenguajes y paqueterías que reportaron los mejores tiempos. Cualquier código siguiente presenta muy buen desempeño en tal implementación. Las diferencias de tiempos entre los códigos son pequeñas y se sugiere volver a correr los códigos midiendo tiempos con paqueterías que permitan la repetición de las mediciones como timeit.

Lenguaje	Código
Python	Rcf_numba_parallel
Python	Rcf_5_cython_openmp
Julia	Rcf_julia_naive
R	Rcf_Rcpp
Python	Rcf_5_cython
Julia	Rcf_julia_typed_values
Python	Rcf_numba
Python	Rcf_numpy
C	Rcf_c

Ejercicio

Presentar una tabla de resúmen de tiempos para las implementaciones pedidas en los ejercicios anteriores.

Referencias de interés

• Cython.

• introduction to cython.

• Basic cython tutorial

• Source files and compilation

• Compiling with a jupyter notebook

• hpy-kick-off-sprint-report

• PyPy - FAQ

• Glossary: virtual machine

• Glossary: Cpython

• Glossary: bytecode.

• Python interpreter, what-is-interpreter-explain-how-python-interpreter-works

• what-is-runtime-in-context-of-python-what-does-it-consist-of

• numba: performance tips, numba: generators

• Dirk Eddelbuettel: rcpp .

• rcpp.org

• Rcpp for everyone.

• Introduction to rcpp:From Simple Examples to Machine Learning.

• Rcpp note.

• Rcpp quick reference guide.

• should-i-prefer-rcppnumericvector-over-stdvector

• rcppparallel-getting-r-and-c-to-work-some-more-in-parallel

• Learncpp.

• Cplusplus.

• what-are-the-downsides-of-jit-compilation

Ejercicios

1.Resuelve los ejercicios y preguntas de la nota.

Referencias:

1. M. Gorelick, I. Ozsvald, High Performance Python, O’Reilly Media, 2014.

2. H. Wickham, Advanced R, 2014

3. B. W. Kernighan, D. M. Ritchie, The C Programming Language, Prentice Hall Software Series, 1988

4. C