1.6 Polinomios de Taylor y diferenciación numérica

Notas para contenedor de docker:

Comando de docker para ejecución de la nota de forma local:

nota: cambiar <ruta a mi directorio> por la ruta de directorio que se desea mapear a /datos dentro del contenedor de docker y <versión imagen de docker> por la versión más actualizada que se presenta en la documentación.

docker run --rm -v <ruta a mi directorio>:/datos --name jupyterlab_optimizacion -p 8888:8888 -d palmoreck/jupyterlab_optimizacion:<versión imagen de docker>

password para jupyterlab: qwerty

Detener el contenedor de docker:

docker stop jupyterlab_optimizacion

Documentación de la imagen de docker palmoreck/jupyterlab_optimizacion:<versión imagen de docker> en liga.

---

Nota generada a partir de la liga1, liga2 e inicio de liga3.

Al final de esta nota la comunidad lectora:

• Aprenderá que el método de diferenciación finita es un método inestable numéricamente respecto al redondeo.

• Conocerá las expresiones de los polinomios de Taylor para funciones de varias variables.

• Tendrá en su lista de programas del lenguaje R implementaciones para aproximar al gradiente y a la Hessiana de una función con los métodos de diferenciación finita.

• Utilizará las fórmulas para calcular errores absolutos y relativos para valores y vectores revisadas en fórmulas para calcular errores absolutos y relativos

Problema: ¿Cómo aproximar una función $f$ en un punto $x_1$?

Si $f$ es continuamente diferenciable en $x_0$ y $f^{(1)},f^{(2)}$ existen y están acotadas en $x_0$ entonces:

$$f(x_1)\approx f(x_0)+f^{(1)}(x_0)(x_1-x_0)$$

y se nombra aproximación de orden 1. Ver Definición de función, continuidad y derivada para definición de continuidad, diferenciabilidad y propiedades.

Comentarios

• Lo anterior requiere de los valores: $x_0,x_1,f(x_0),f^{(1)}(x_0)$. Esta aproximación tiene un error de orden $2$ pues su error es proporcional al cuadrado del ancho del intervalo: $h=x_1-x_0$, esto es, si reducimos a la mitad $h$ entonces el error se reduce en una cuarta parte.

• Otra aproximación más simple sería:

$$f(x_1)\approx f(x_0)$$

lo cual sólo requiere del conocimiento de $f(x_0)$ y se nombra aproximación de orden $0$, sin embargo esta aproximación tiene un error de orden $1$ pues este es proporcional a $h$ , esto es, al reducir a la mitad $h$ se reduce a la mitad el error.

• Los errores anteriores los nombramos errores por truncamiento, ver Fuentes del error y Análisis del error para un recordatorio de tal error. Utilizamos la notación “O grande” $\mathcal{O}(\cdot )$ para escribir lo anterior:

$$f(x)-f(x_0)=\mathcal{O}(h)$$

con la variable $h=x-x_0$. En este caso se representa a un error de orden $1$. Análogamente:

$$f(x)-(f(x_0)+f^{(1)}(x_0)(x-x_0))=\mathcal{O}(h^2)$$

y se representa un error de orden $2$.

Observaciones

• No confundir órdenes de una aproximación con órdenes de error.

• Otras aproximaciones a una función se pueden realizar con:

  • Interpoladores polinomiales (representación por Vandermonde, Newton, Lagrange).

Aproximación a una función por el teorema de Taylor

En esta sección se presenta el teorema de Taylor, el cual, bajo ciertas hipótesis nos proporciona una expansión de una función alrededor de un punto. Este teorema será utilizado en diferenciación e integración numérica. El teorema es el siguiente:

Teorema de Taylor

Sea $f:\mathbb{R}\to \mathbb{R}$, $f\in {\mathcal{C}}^n([a,b])$ tal que $f^{(n+1)}$ existe en [a,b]. Si $x_0\in [a,b]$ entonces $\mathrm{\forall }x\in [a,b]$ se tiene: $f(x)=P_n(x)+R_n(x)$ donde:

$$P_n(x)={\displaystyle \sum _{k=0}^n\frac{f^{(k)}(x_0)(x-x_0{)}^k}{k!}(f^{(0)}=f)}$$

$$R_n(x)=\frac{f^{(n+1)}({\xi }_x)(x-x_0{)}^{(n+1)}}{(n+1)!}$$

con ${\xi }_x$ entre $x_0,x$ y $x_0$ se llama centro. Ver Definición de función, continuidad y derivada para definición del conjunto ${\mathcal{C}}^n([a,b])$.

Comentarios

• El teorema de Taylor nos indica que cualquier función suave (función en ${\mathcal{C}}^n)$ se le puede aproximar por un polinomio en el intervalo $[a,b]$, de hecho $f(x)\approx P_n(x)$.

• Si el residuo no tiene una alta contribución a la suma $P_n(x)+R_n(x)$ entonces es una buena aproximación local (alta contribución y buena aproximación depende de factores como elección de la norma y la aplicación).

• El teorema de Taylor es una generalización del teorema del valor medio para derivadas.

• $P_n(x)$ se le llama polinomio de Taylor alrededor de $x_0$ de orden $n$ y $R_n(x)$ es llamado residuo de Taylor alrededor de $x_0$ de orden $n+1$, tiene otras expresiones para representarlo y la que se utiliza en el enunciado anterior es en su forma de Lagrange (ver liga para otras expresiones del residuo).

• ${\xi }_x$ es un punto entre $x_0,x$ desconocido y está en función de $x$ (por eso se le escribe un subíndice).

• Una forma del teorema de Taylor es escribirlo definiendo a la variable $h=x-x_0$:

$$f(x)=f(x_0+h)=P_n(h)+R_n(h)={\displaystyle \sum _{k=0}^n\frac{f^{(k)}(x_0)h^k}{k!}+\frac{f^{(n+1)}({\xi }_h)h^{n+1}}{(n+1)!}}$$

y si $f^{(n+1)}$ es acotada, escribimos: $R_n(h)=\mathcal{O}(h^{n+1})$.

Ejemplo

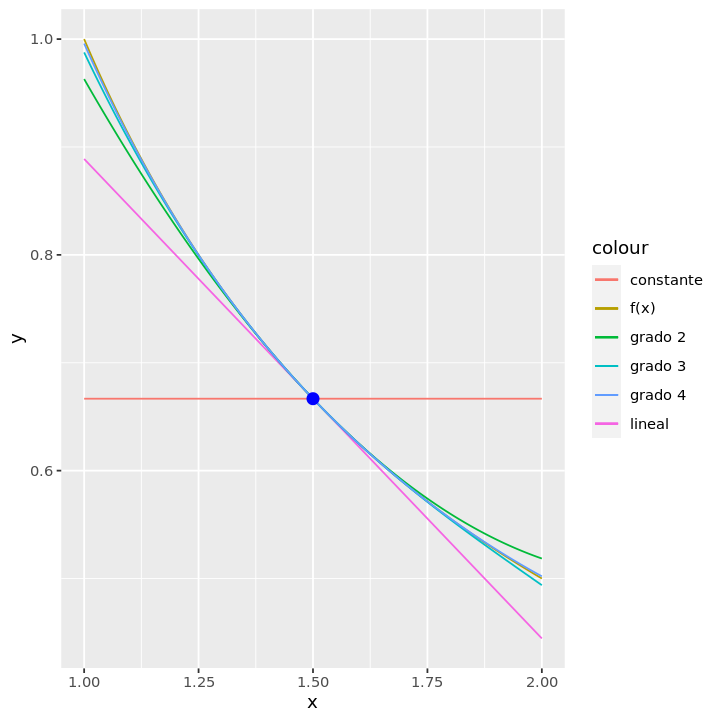
Graficar la función y los polinomios de Taylor de grados $0,1,2,3$ y $4$ en una sola gráfica para el intervalo $[1,2]$ de la función $\frac{1}{x}$ con centro en $x_0=1.5$. ¿Cuánto es la aproximación de los polinomios en x=1.9?. Calcula el error relativo de tus aproximaciones.

Solución

Obtengamos los polinomios de Taylor de orden $n$ con $n\in \{0,1,2,3\}$ y centro en $x_0=1.5$ para la función $\frac{1}{x}$ en el intervalo $[1,2]$. Los primeros tres polinomios de Taylor son:

$$P_0(x)=f(x_0)=\frac{2}{3}\text{(constante)}$$

$$P_1(x)=f(x_0)+f^{(1)}(x_0)(x-x_0)=\frac{2}{3}-\frac{1}{x_0^2}(x-x_0)=\frac{2}{3}-\frac{1}{{1.5}^2}(x-1.5)\text{(lineal)}$$

$$\begin{array}{r}\begin{array}{rcl}{P}_2(x)& =& f(x_0)+f^{(1)}(x_0)(x-x_0)+\frac{f^{(2)}(x_0)(x-x_0{)}^2}{2}\\ & =& \frac{2}{3}-\frac{1}{x_0^2}(x-x_0)+\frac{1}{x_0^3}(x-x_0{)}^2\\ & =& \frac{2}{3}-\frac{1}{{1.5}^2}(x-1.5)+\frac{1}{{1.5}^3}(x-1.5{)}^2\text{(cuadrático)}\end{array}\end{array}$$

library(ggplot2)

options(repr.plot.width=6, repr.plot.height=6) #esta línea sólo se ejecuta para jupyterlab con R

Taylor_approx <- function(x,c,n){
    '
    Taylor approximation for 1/x function. Will return Taylor polynomial of degree n with
    center in c and evaluated in x.
    Args:
        x (double): numeric vector or scalar in which Taylor polynomial will be evaluated. 
        c (double): scalar which represents center of Taylor polynomial of degree n.
        n (integer): scalar which represents degree of Taylor polynomial. 
    Returns:
        sum (double): scalar evaluation of Taylor polynomial of degree n with center c in x.
    '
    length_x <- length(x)
    sum <- vector("double", length_x)
    for(j in 1:length_x){
        mult <- c^(-1)
        sum[j] <- mult
        for(k in 1:n){
            mult <- -1*c^(-1)*(x[j]-c)*mult
            sum[j] <- sum[j] + mult
            }
    }
    sum #accumulated sum
}

x0 <- 1.5
x <- seq(from=1,to=2,by=.005)
n <- c(0,1,2,3,4) #degrees of Taylor polynomials
f <- function(z)1/z
y <- f(x)
y_Taylor_0 <- f(x0)*(vector("double", length(x))+1)
y_Taylor_1 <- Taylor_approx(x,x0,1)
y_Taylor_2 <- Taylor_approx(x,x0,2)
y_Taylor_3 <- Taylor_approx(x,x0,3)
y_Taylor_4 <- Taylor_approx(x,x0,4)

gg <- ggplot()

print(gg+
geom_line(aes(x=x,y=y,color='f(x)')) + 
geom_line(aes(x=x,y=y_Taylor_0,color='constante'))+
geom_line(aes(x=x,y=y_Taylor_1,color='lineal')) + 
geom_line(aes(x=x,y=y_Taylor_2,color='grado 2')) + 
geom_line(aes(x=x,y=y_Taylor_3,color='grado 3')) +
geom_line(aes(x=x,y=y_Taylor_4,color='grado 4')) + 
geom_point(aes(x=x0, y=f(x0)), color='blue',size=3))

Observación

Para cualquier aproximación calculada siempre es una muy buena idea reportar el error relativo de la aproximación si tenemos el valor del objetivo. No olvidar esto :)

Para el cálculo del error utilizamos fórmulas para calcular errores absolutos y relativos:

$$\text{ErrRel(aprox)}=\frac{|\text{aprox}-\text{obj}|}{|\text{obj}|}$$

La siguiente función calcula un error relativo para un valor obj:

compute_error_point_wise<-function(obj, approx){
    '
    Relative or absolute error between approx and obj in a point wise fashion.
    
    '
    if (abs(obj) > .Machine$double.eps*.Machine$double.xmin){
        Err<-abs(obj-approx)/abs(obj)
    }else
        Err<-abs(obj-approx)
    Err
}

x_test_point <- 1.9
objective <- f(x_test_point)
#Approximations
p1_approx <- Taylor_approx(x_test_point, x0, 1)
p2_approx <- Taylor_approx(x_test_point, x0, 2)
p3_approx <- Taylor_approx(x_test_point, x0, 3)
p4_approx <- Taylor_approx(x_test_point, x0, 4)

print('error relativo polinomio constante')
print(compute_error_point_wise(objective, 1/x0))
print('error relativo polinomio lineal')
print(compute_error_point_wise(objective, p1_approx))
print('error relativo polinomio grado 2')
print(compute_error_point_wise(objective, p2_approx))
print('error relativo polinomio grado 3')
print(compute_error_point_wise(objective, p3_approx))
print('error relativo polinomio grado 4')
print(compute_error_point_wise(objective, p4_approx))

[1] "error relativo polinomio constante"
[1] 0.2666667
[1] "error relativo polinomio lineal"
[1] 0.07111111
[1] "error relativo polinomio grado 2"
[1] 0.01896296
[1] "error relativo polinomio grado 3"
[1] 0.00505679
[1] "error relativo polinomio grado 4"
[1] 0.001348477

Ejercicio

Utilizando lenguajes de programación aproximar $f(1)$ con polinomios de Taylor de orden $0,1,2,3,4$ si $f(x)=-0.1x^4-0.15x^3-0.5x^2-0.25x+1.2$ con centro en $x0=0$. Calcula los errores relativos de tus aproximaciones. Realiza las gráficas de cada polinomio en el intervalo $[0,1]$ con ggplot2. Observa que $R_5(x)$ es cero.

Teorema de Taylor para una función $f:{\mathbb{R}}^n\to \mathbb{R}$

Sea $f:{\mathbb{R}}^n\to \mathbb{R}$ diferenciable en $\text{dom}f$. Si $x_0,x\in \text{dom}f$ y $x_0+t(x-x_0)\in \text{dom}f,\mathrm{\forall }t\in (0,1),$ entonces $\mathrm{\forall }x\in \text{dom}f$ se tiene $f(x)=P_0(x)+R_0(x)$ donde:

$$P_0(x)=f(x_0)$$

$$R_0(x)=\mathrm{\nabla }f(x_0+t_x(x-x_0){)}^T(x-x_0)$$

para alguna $t_x\in (0,1)$ y $\mathrm{\nabla }f(\cdot )$ gradiente de $f$, ver Definición de función, continuidad y derivada para definición del gradiente de una función.

Observación

La aproximación anterior la nombramos aproximación de orden $0$ para $f$ con centro en $x_0$. Si $\mathrm{\nabla }f(\cdot )$ es acotado en $\text{dom}f$ entonces se escribe: $R_0(x)=\mathcal{O}(||x-x_0||)$.

Si además $f$ es continuamente diferenciable en $\text{dom}f$(su derivada es continua, ver Definición de función, continuidad y derivada para definición de continuidad), $f^{(2)}$ existe en $\text{dom}f$, se tiene $f(x)=P_1(x)+R_1(x)$ donde:

$$P_1(x)=f(x_0)+\mathrm{\nabla }f(x_0{)}^T(x-x_0)$$

$$R_1(x)=\frac{1}{2}(x-x_0{)}^T{\mathrm{\nabla }}^{2}f(x_0+t_x(x-x_0))(x-x_0)$$

para alguna $t_x\in (0,1)$ y ${\mathrm{\nabla }}^{2}f(\cdot )$ Hessiana de $f$ (ver Definición de función, continuidad y derivada para definición de la matriz Hessiana).

Observación

La aproximación anterior la nombramos aproximación de orden $1$ para $f$ con centro en $x_0$. Si ${\mathrm{\nabla }}^{2}f(\cdot )$ es acotada en $\text{dom}f$ entonces se escribe: $R_1(x)=\mathcal{O}(||x-x_0|{|}^2)$.

Si $f^{(2)}$ es continuamente diferenciable y $f^{(3)}$ existe y es acotada en $\text{dom}f$, se tiene $f(x)=P_2(x)+R_2(x)$ donde:

$$P_2(x)=f(x_0)+\mathrm{\nabla }f(x_0{)}^T(x-x_0)+\frac{1}{2}(x-x_0{)}^T{\mathrm{\nabla }}^{2}f(x_0)(x-x_0)$$

Observación

• La aproximación anterior la nombramos aproximación de orden $2$ para $f$ con centro en $x_0$. Para las suposiciones establecidas se tiene:

$$R_2(x)=\mathcal{O}(||x-x_0|{|}^3).$$

• En este caso $f^{(3)}$ es un tensor.

Comentario

Tomando $h=x-x_0$, se reescribe el teorema como sigue, por ejemplo para la aproximación de orden $1$ incluyendo su residuo:

$$f(x)=f(x_0+h)=\underset{P_1(h)}{\underbrace{f(x_0)+\mathrm{\nabla }f(x_0{)}^{T}h}}+\underset{R_1(h)}{\underbrace{\frac{1}{2}{h}^T{\mathrm{\nabla }}^{2}f(x_0+t_{x}h)h}}.$$

Si $f^{(2)}$ es acotada en $\text{dom}f$, escribimos: $R_1(h)=\mathcal{O}(||h|{|}^2)$.

Diferenciación numérica por diferencias finitas

Comentario

En esta sección se revisan métodos numéricos para aproximar las derivadas. Otros métodos para el cálculo de las derivadas se realizan con el cómputo simbólico o algebraico, ver Definición de función, continuidad y derivada para ejemplos.

Las fórmulas de aproximación a las derivadas por diferencias finitas pueden obtenerse con los polinomios de Taylor, presentes en el teorema del mismo autor, por ejemplo:

Sea $f\in {\mathcal{C}}^1([a,b])$ y $f^{(2)}$ existe y está acotada $\mathrm{\forall }x\in [a,b]$ entonces, si $x+h\in [a,b]$ con $h>0$ por el teorema de Taylor:

$$f(x+h)=f(x)+f^{(1)}(x)h+f^{(2)}({\xi }_{x+h})\frac{h^2}{2}$$

con ${\xi }_{x+h}\in [x,x+h]$ y al despejar $f^{(1)}(x)$ se tiene:

$$f^{(1)}(x)=\frac{f(x+h)-f(x)}{h}-f^{(2)}({\xi }_{x+h})\frac{h}{2}.$$

y escribimos:

$$f^{(1)}(x)=\frac{f(x+h)-f(x)}{h}+\mathcal{O}(h).$$

La aproximación $\frac{f(x+h)-f(x)}{h}$ es una fórmula por diferencias hacia delante con error de orden $1$. Gráficamente se tiene:

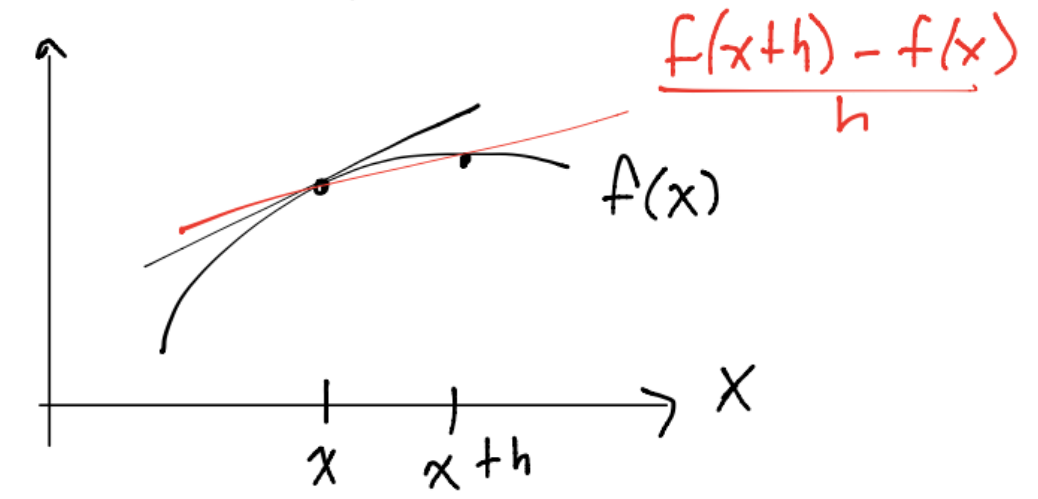
Con las mismas suposiciones es posible obtener la fórmula para la aproximación por diferencias hacia atrás:

$$f^{(1)}(x)=\frac{f(x)-f(x-h)}{h}+\mathcal{O}(h),h>0.$$

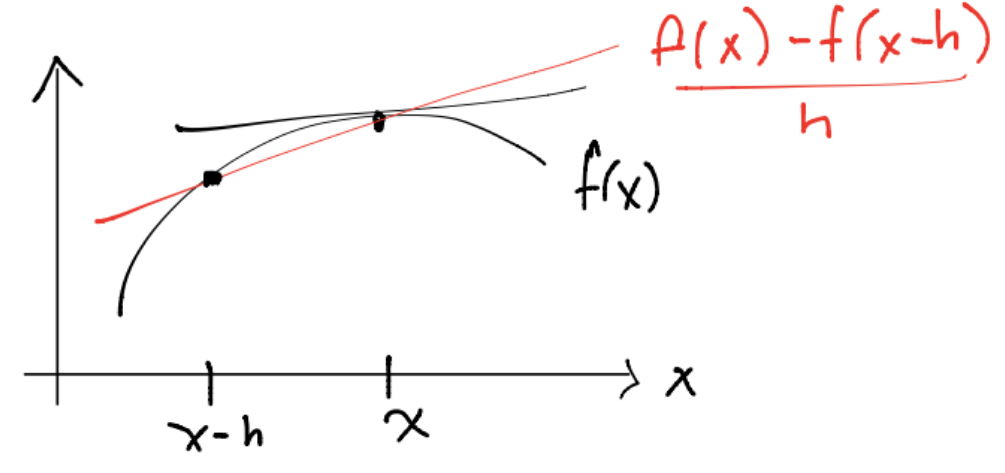
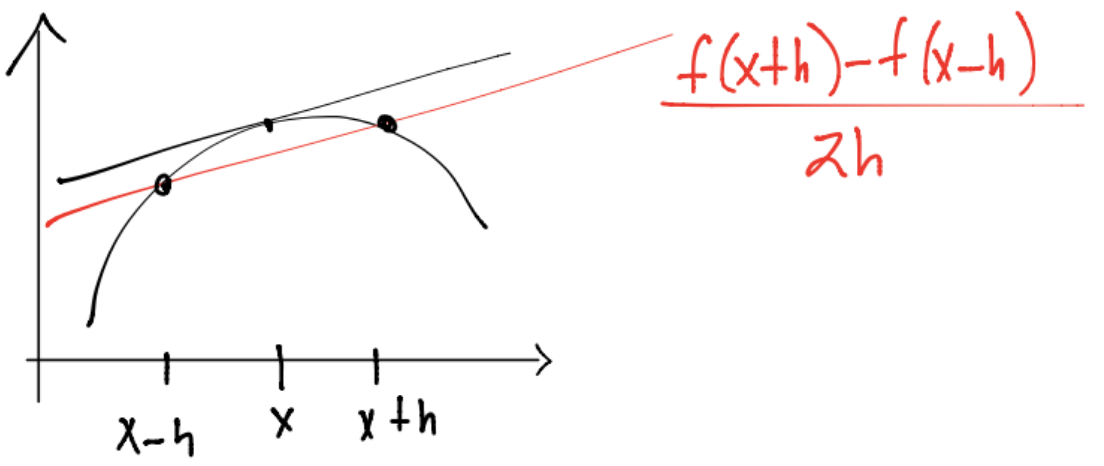
Considerando $f\in {\mathcal{C}}^2([a,b]),f^{(3)}$ existe y está acotada $\mathrm{\forall }x\in [a,b]$ si $x-h,x+h\in [a,b]$ y $h>0$ entonces:

$$f^{(1)}(x)=\frac{f(x+h)-f(x-h)}{2h}+\mathcal{O}(h^2),h>0.$$

y el cociente $\frac{f(x+h)-f(x-h)}{2h}$ es la aproximación por diferencias centradas con error de orden $2$. Gráficamente:

Observaciones

• La aproximación por diferencias finitas a la primer derivada de la función tiene un error de orden $\mathcal{O}(h)$ por lo que una elección de $h$ igual a $.1={10}^{-1}$ generará aproximaciones con alrededor de un dígito correcto.

• La diferenciación numérica por diferencias finitas no es un proceso con una alta exactitud pues los problemas del redondeo de la aritmética en la máquina se hacen presentes en el mismo (ver nota Sistema de punto flotante). Como ejemplo de esta situación realicemos el siguiente ejemplo.

Ejemplo

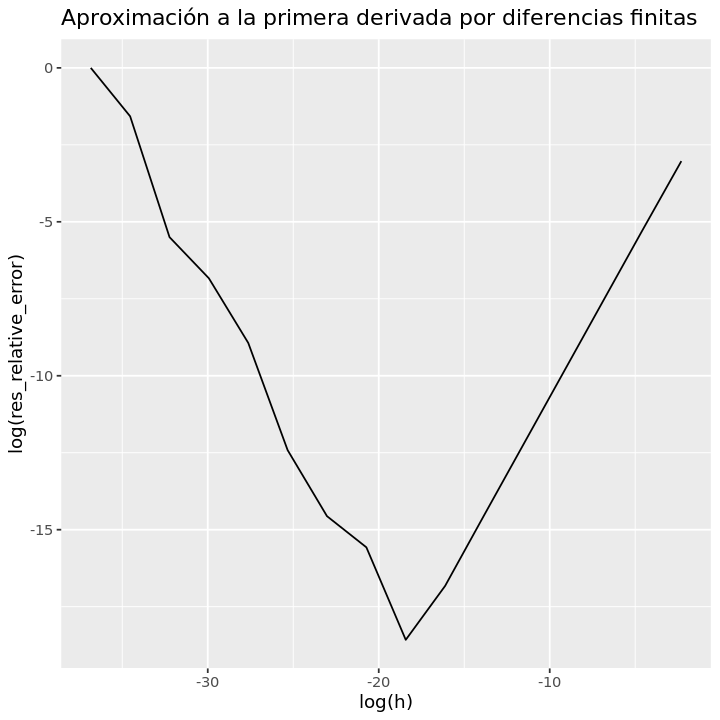
Realizar una gráfica de log(error relativo) vs log(h) (h en el eje horizontal) para aproximar la primera derivada de $f(x)=e^{-x}$ en $x=1$ con $h\in \{{10}^{-16},{10}^{-15},\dots ,{10}^{-1}\}$ y diferencias hacia delante. Valor a aproximar: $f^{(1)}(1)=-e^{-1}$.

Definimos la función

f <- function(x){
     exp(-x)
     }

Definimos la aproximación numérica por diferencias finitas a la primera derivada

approx_first_derivative <- function(f, x, h){    
    '
    Numerical differentiation by finite differences. Uses forward point formula
    to approximate first derivative of function.
    Args:
        f (function): function definition.
        x (float): point where first derivative will be approximated
        h (float): step size for forward differences. Tipically less than 1
    Returns:
        res (float): approximation to first_derivative.
    '
    res <- (f(x+h)-f(x))/h
    res
    }

Puntos donde se evaluará la aproximación:

x<-1

h<-10^(-1*(1:16))

Aproximación numérica:

approx_df <- approx_first_derivative(f,x,h)

Derivada de la función:

df<-function(x){
    -exp(-x)
}

obj_df <- df(x)

Cálculo de errores:

res_relative_error <- compute_error_point_wise(obj_df, approx_df)

Gráfica:

gf <- ggplot()

print(gf+
geom_line(aes(x=log(h),y=log(res_relative_error)))+
ggtitle('Aproximación a la primera derivada por diferencias finitas'))

Ejercicio

Utilizando lenguajes de programación realizar una gráfica de log(error relativo) vs log(h) (h en el eje horizontal) con ggplot2 para aproximar la segunda derivada de $f(x)=e^{-x}$ en $x=1$ con $h\in \{{10}^{-16},{10}^{-14},\dots ,{10}^{-1}\}$ y diferencias hacia delante. Valor a aproximar: $f^{(2)}(1)=e^{-1}$. Usar:

$$\frac{d^{2}f(x)}{dx}=\frac{f(x+2h)-2f(x+h)+f(x)}{h^2}+\mathcal{O}(h)$$

Encontrar valor(es) de $h$ que minimiza(n) al error absoluto y relativo.

Comentario

Aproximaciones a la segunda derivada de una función $f:\mathbb{R}\to \mathbb{R}$ se pueden obtener con las fórmulas:

• $\frac{d^{2}f(x)}{dx}=\frac{f(x+2h)-2f(x+h)+f(x)}{h^2}+\mathcal{O}(h)$ por diferencias hacia delante.

• $\frac{d^{2}f(x)}{dx}=\frac{f(x)-2f(x-h)+f(x-2h)}{h^2}+\mathcal{O}(h)$ por diferencias hacia atrás.

• $\frac{d^{2}f(x)}{dx}=\frac{f(x+h)-2f(x)+f(x-h)}{h^2}+\mathcal{O}(h^2)$ por diferencias centradas.

Estas fórmulas se obtienen con el teorema de Taylor bajo las suposiciones correctas.

Análisis del error por redondeo y truncamiento en la aproximación por diferencias finitas hacia delante

El ejemplo anterior muestra (vía una gráfica) que el método numérico de diferenciación numérica no es estable numéricamente respecto al redondeo (ver nota Condición de un problema y estabilidad de un algoritmo para definición de estabilidad de un algoritmo) y también se puede corroborar realizando un análisis del error. En esta sección consideramos la aproximación a la primer derivada por diferencias finitas hacia delante:

$$\frac{f(x+h)-f(x)}{h}$$

Suponemos que $\hat{f}(x)$ aproxima a $f(x)$ y por errores de redondeo $\hat{f}(x)=f(x)(1+{ϵ}_{f(x)})$ con $|{ϵ}_{f(x)}|\le {ϵ}_{maq}$ error de redondeo al evaluar $f$ en $x$. $\hat{f}(x)$ es la aproximación en un SPFN (ver nota Sistema de punto flotante). Además supóngase que $x,x+h,h\in \mathcal{Fl}$ . Entonces en la aproximación a la primer derivada por diferencias hacia delante:

$f^{(1)}(x)=\frac{f(x+h)-f(x)}{h}+\mathcal{O}(h)$ y calculando el error absoluto:

$$\begin{array}{r}\begin{array}{rcl}\text{ErrAbs}\left(\frac{\hat{f}(x+h)-\hat{f}(x)}{h}\right)& =& |f^{(1)}(x)-\frac{\hat{f}(x+h)-\hat{f}(x)}{h}|\\ & =& |\frac{f(x+h)-f(x)}{h}+\mathcal{O}(h)-\left(\frac{f(x+h)(1+{ϵ}_{f(x+h)})-f(x)(1+{ϵ}_{f(x)})}{h}\right)|\\ & =& |\mathcal{O}(h)-\frac{f(x+h){ϵ}_{f(x+h)}-f(x){ϵ}_{f(x)}}{h}|\\ & \le & \mathcal{O}(h)+\frac{C{ϵ}_{maq}}{h}\end{array}\end{array}$$

suponiendo en el último paso que $|f(x+h){ϵ}_{f(x+h)}-f(x){ϵ}_{f(x)}|\le C{ϵ}_{maq}$ con $C>0$ constante que acota a la función $f$ en el intervalo $[a,b]$. Obsérvese que $\frac{\hat{f}(x+h)-\hat{f}(x)}{h}$ es la aproximación a la primer derivada por diferencias hacia delante que se obtiene en la computadora, por lo que la cantidad $|f^{(1)}(x)-\frac{\hat{f}(x+h)-\hat{f}(x)}{h}|$ es el error absoluto de tal aproximación.

El error relativo es:

$$\text{ErrRel}\left(\frac{\hat{f}(x+h)-\hat{f}(x)}{h}\right)=\frac{\text{ErrAbs}\left(\frac{\hat{f}(x+h)-\hat{f}(x)}{h}\right)}{|f^{(1)}(x)|}\le \frac{\mathcal{O}(h)+\frac{C{ϵ}_{maq}}{h}}{|f^{(1)}(x)|}=K_{1}h+K_2\frac{1}{h}$$

con $K_1,K_2>0$ constantes.

Entonces la función $g(h)=\mathcal{O}(h)+\mathcal{O}\left(\frac{1}{h}\right)$ acota al error absoluto y al error relativo y se tiene:

• Si $h\to 0$ la componente $\mathcal{O}\left(\frac{1}{h}\right)$ domina a la componente $\mathcal{O}(h)$, la cual tiende a $0$.

• Si $h\to \mathrm{\infty }$ la componente $\mathcal{O}(h)$ domina a $\mathcal{O}\left(\frac{1}{h}\right)$, la cual tiende a $0$.

Por lo anterior, existe un valor de $h$ que minimiza a los errores. Tal valor se observa en las gráficas anteriores y es igual a:

print(h[which.min(res_relative_error)])

[1] 1e-08

Ejercicio

Obtener de forma analítica el valor de $h$ que minimiza la función $g(h)$ anterior. Tip: utilizar criterio de primera y segunda derivada para encontrar mínimo global.

Conclusiones y comentarios

• La componente $\mathcal{O}(h)$ es el error por truncamiento, la cual resulta del teorema de Taylor. El teorema de Taylor nos indica que añadir términos en el polinomio de Taylor si la $x$ a aproximar es cercana al centro, las derivadas de $f$ son acotadas y $h\to 0$ entonces el error por truncamiento debe tender a $0$. Lo anterior no ocurre en la implementación numérica (corroborado de forma analítica y visual) del método por diferenciación numérica para la primer derivada por la presencia de la componente $\mathcal{O}\left(\frac{1}{h}\right)$ en los errores. Tal componente proviene del error por redondeo.

• Obsérvese que el error relativo máximo es del $100\mathrm{\%}$ lo que indica que no se tiene ninguna cifra correcta en la aproximación:

print(max(res_relative_error))

[1] 1

y esto ocurre para un valor de $h$ igual a:

print(h[which.max(res_relative_error)])

[1] 1e-16

Pregunta

¿Por qué se alcanza el máximo error relativo en el valor de $h={10}^{-16}$?.

• Con lo anterior se tiene que la diferenciación numérica es un método inestable numéricamente respecto al redondeo. Ver nota Condición de un problema y estabilidad de un algoritmo.

• Un análisis de error similar se utiliza para el método de diferencias finitas por diferencias centradas para aproximar la primera derivada. En este caso el valor de $h$ que minimiza a los errores es del orden $h^{\ast }={10}^{-6}$.

Diferenciación numérica para una función $f:{\mathbb{R}}^n\to \mathbb{R}$

Supongamos $f$ es dos veces diferenciable en $\text{intdom}f$. Si $f:{\mathbb{R}}^n\to \mathbb{R}$ entonces $\mathrm{\nabla }f:{\mathbb{R}}^n\to {\mathbb{R}}^n$ y ${\mathrm{\nabla }}^{2}f:{\mathbb{R}}^n\to {\mathbb{R}}^{n\times n}$ (ver Definición de función, continuidad y derivada para definición de derivadas en funciones $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$). Ambas funciones al evaluarse resultan en un vector en ${\mathbb{R}}^n$ y en una matriz en ${\mathbb{R}}^{n\times n}$ respectivamente.

Podemos utilizar las fórmulas de aproximación en diferenciación numérica con diferencias finitas para el caso $f:\mathbb{R}\to \mathbb{R}$ revisadas anteriormente para aproximar al gradiente y a la Hessiana.

Para el caso del gradiente se tiene por diferenciación hacia delante:

$$\begin{array}{r}\mathrm{\nabla }f(x)=\begin{array}{l}\left[\begin{array}{c}\frac{\partial f(x)}{\partial x_1}\\ ⋮\\ \frac{\partial f(x)}{\partial x_n}\end{array}\right]\approx ,\mathrm{\nabla }\hat{f}(x)=\left[\begin{array}{c}\frac{f(x+h{e}_1)-f(x)}{h}\\ ⋮\\ \frac{f(x+h{e}_n)-f(x)}{h}\end{array}\right]\end{array}\in {\mathbb{R}}^n\end{array}$$

con $e_j$ $j$-ésimo vector canónico que tiene un número $1$ en la posición $j$ y $0$ en las entradas restantes para $j=1,\dots ,n$. Se cumple $||\mathrm{\nabla }f(x)-\mathrm{\nabla }\hat{f}(x)||=\mathcal{O}(h)$. Y para el caso de la Hessiana:

$$\begin{array}{r}{\mathrm{\nabla }}^{2}f(x)=\left[\begin{array}{cccc}\frac{{\partial }^{2}f(x)}{\partial x_1^2}& \frac{{\partial }^{2}f(x)}{\partial x_2\partial x_1}& \dots & \frac{{\partial }^{2}f(x)}{\partial x_n\partial x_1}\\ \frac{{\partial }^{2}f(x)}{\partial x_1\partial x_2}& \frac{{\partial }^{2}f(x)}{\partial x_2^2}& \dots & \frac{{\partial }^{2}f(x)}{\partial x_n\partial x_2}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}f(x)}{\partial x_1\partial x_n}& \frac{{\partial }^{2}f(x)}{\partial x_2\partial x_n}& \dots & \frac{{\partial }^{2}f(x)}{\partial x_n^2}\end{array}\right],\end{array}$$

$$\begin{array}{r}{\mathrm{\nabla }}^2\hat{f}(x)=\left[\begin{array}{cccc}\frac{f(x+2h{e}_1)-2f(x+h{e}_1)+f(x)}{h^2}& \frac{f(x+h{e}_1+h{e}_2)-f(x+h{e}_1)-f(x+h{e}_2)+f(x)}{h^2}& \dots & \frac{f(x+h{e}_1+h{e}_n)-f(x+h{e}_1)-f(x+h{e}_n)+f(x)}{h^2}\\ \frac{f(x+h{e}_1+h{e}_2)-f(x+h{e}_2)-f(x+h{e}_1)+f(x)}{h^2}& \frac{f(x+2h{e}_2)-2f(x+h{e}_2)+f(x)}{h^2}& \dots & \frac{f(x+h{e}_2+h{e}_n)-f(x+h{e}_2)-f(x+h{e}_n)+f(x)}{h^2}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{f(x+h{e}_1+h{e}_n)-f(x+h{e}_n)-f(x+h{e}_1)+f(x)}{h^2}& \frac{f(x+h{e}_2+h{e}_n)-f(x+h{e}_n)-f(x+h{e}_2)+f(x)}{h^2}& \dots & \frac{f(x+2h{e}_n)-2f(x+h{e}_n)+f(x)}{h^2}\end{array}\right]\end{array}$$

Se cumple: $||{\mathrm{\nabla }}^{2}f(x)-\mathrm{\nabla }{\hat{f}}^2(x)||=\mathcal{O}(h)$.

Ejemplo

Aproximar $\mathrm{\nabla }f(x),{\mathrm{\nabla }}^{2}f(x)$ con diferencias hacia delante y $h\in \{{10}^{-16},{10}^{-14},\dots ,{10}^{-1}\}$ para $f:{\mathbb{R}}^4\to \mathbb{R}$, dada por $f(x)=(x_1^2-x_2^2{)}^2+x_1^2+(x_3^2-x_4^2{)}^2+x_3^2$ en el punto $x_0=(1.5,1.5,1.5,1.5{)}^T$. Realizar una gráfica de $\log ($Err_rel) vs $\log ($h)

Para esta función se tiene:

$$\begin{array}{r}\mathrm{\nabla }f(x)=\left[\begin{array}{c}4x_1(x_1^2-x_2^2)+2x_1\\ -4x_2(x_1^2-x_2^2)\\ 4x_3(x_3^2-x_4^2)+2x_3\\ -4x_4(x_3^2-x_4^2)\end{array}\right],\end{array}$$

$$\begin{array}{r}{\mathrm{\nabla }}^{2}f(x)=\left[\begin{array}{cccc}12x_1^2-4x_2^2+2& -8x_1{x}_2& 0& 0\\ -8x_1{x}_2& -4x_1^2+12x_2^2& 0& 0\\ 0& 0& 12x_3^2-4x_4^2+2& -8x_3{x}_4\\ 0& 0& -8x_3{x}_4& -4x_3^2+12x_4^2\end{array}\right]\end{array}$$

Gradiente de f calculado de forma simbólica

gf<-function(x){
    c(4*x[1]*(x[1]^2-x[2]^2)+2*x[1],
      -4*x[2]*(x[1]^2-x[2]^2),
      4*x[3]*(x[3]^2-x[4]^2)+2*x[3],
      -4*x[4]*(x[3]^2-x[4]^2))
}

Punto en el que se evaluará

x_0<-c(1.5,1.5,1.5,1.5)

print(gf(x_0))

[1] 3 0 3 0

$$\begin{array}{r}\mathrm{\nabla }f(x_0)=\left[\begin{array}{c}3\\ 0\\ 3\\ 0\end{array}\right],\end{array}$$

Hessiana de f calculada de forma simbólica

gf2<-function(x){
    matrix(c(12*x[1]^2-4*x[2]^2+2,-8*x[1]*x[2],0,0,
             -8*x[1]*x[2],-4*x[1]^2+12*x[2]^2,0,0,
             0,0,12*x[3]^2-4*x[4]^2+2,-8*x[3]*x[4],
             0,0,-8*x[3]*x[4],-4*x[3]^2+12*x[4]^2),nrow=4,ncol=4)
}

Evaluación de la Hessiana

print(gf2(x_0))

     [,1] [,2] [,3] [,4]
[1,]   20  -18    0    0
[2,]  -18   18    0    0
[3,]    0    0   20  -18
[4,]    0    0  -18   18

$$\begin{array}{r}{\mathrm{\nabla }}^{2}f(x_0)=\left[\begin{array}{cccc}20& -18& 0& 0\\ -18& 18& 0& 0\\ 0& 0& 20& -18\\ 0& 0& -18& 18\end{array}\right]\end{array}$$

Definición de función y punto en el que se calculan las aproximaciones

f <- function(x){
    (x[1]^2-x[2]^2)^2+x[1]^2+(x[3]^2-x[4]^2)^2+x[3]^2
    }
x0 <- rep(1.5,4)

Lo siguiente calcula el gradiente y la Hessiana de forma numérica con la aproximación por diferencias hacia delante

inc_index<-function(vec,index,h){
    '
    Auxiliary function for gradient and Hessian computation.
    Args:
        vec (double): vector
        index (int): index.
        h (float):   quantity that vec[index] will be increased.
    Returns:
        vec (double): vector with vec[index] increased by h.
    '
    vec[index]<-vec[index]+h
    vec
}

gradient_approximation<-function(f,x,h=1e-8){
    '
    Numerical approximation of gradient for function f using forward differences.
    Args:
        f (function): definition of function f.
        x (double): vector that holds values where gradient will be computed.
        h (float): step size for forward differences, tipically h=1e-8
    Returns:
        gf (array): numerical approximation to gradient of f.
    '
    n<-length(x)
    gf<-vector("double",n)
    for(i in 1:n){
        gf[i]=(f(inc_index(x,i,h))-f(x))
    }
    gf/h
}

Hessian_approximation<-function(f,x,h=1e-6){
    '
    Numerical approximation of Hessian for function f using forward differences.
    Args:
        f (function): definition of function f.
        x (double): vector that holds values where Hessian will be computed.
        h (float): step size for forward differences, tipically h=1e-6
    Returns:
        Hf (double): matrix of numerical approximation to Hessian of f.
    '
    n<-length(x)
    Hf<-matrix(rep(0,n^2),nrow=n,ncol=n)
    f_x<-f(x)
    for(i in 1:n){
        x_inc_in_i<-inc_index(x,i,h)
        f_x_inc_in_i<-f(x_inc_in_i)
        for(j in i:n){
            dif<-f(inc_index(x_inc_in_i,j,h))-f_x_inc_in_i-f(inc_index(x,j,h))+f_x
            Hf[i,j]<-dif
            if(j!=i)
                Hf[j,i]<-dif
        }
    }
    Hf/h^2
}

Conjunto de valores de h para diferencias hacia delante

h<-10^(-1*(1:16))

Para el cálculo del error utilizamos fórmulas para calcular errores absolutos y relativos:

$$\text{ErrRel(aprox)}=\frac{||\text{aprox}-\text{obj}||}{||\text{obj}||}$$

La siguiente función calcula un error relativo para un vector obj:

Euclidian_norm<-function(vec){
    'Compute Euclidian norm of vector'
    sqrt(sum(vec*vec))
}

compute_error<-function(obj,approx){
    '
    Relative or absolute error between obj and approx based in Euclidian norm. 
    Approx is a numeric vector.
    '
    if (Euclidian_norm(obj) > .Machine$double.eps*.Machine$double.xmin){
        Err<-Euclidian_norm(obj-approx)/Euclidian_norm(obj)
    }else
        Err<-Euclidian_norm(obj-approx)
    Err
}

gf_numeric_approximations <- lapply(h,gradient_approximation,f=f,x=x0)
gf2_numeric_approximations <- lapply(h,Hessian_approximation,f=f,x=x0)


rel_err_gf <- sapply(gf_numeric_approximations,compute_error,obj=gf(x_0))

rel_err_gf2 <- sapply(gf2_numeric_approximations,compute_error,obj=gf2(x_0))

gg<-ggplot()

print(gg+
geom_line(aes(x=log(h),y=log(rel_err_gf)))+
ggtitle('Aproximación al gradiente por diferencias finitas'))

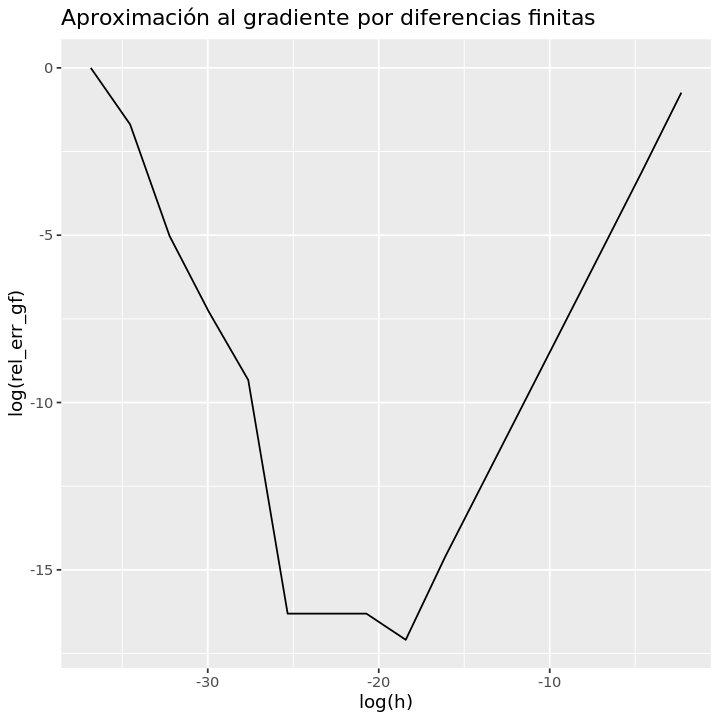
print(h[which.min(rel_err_gf)])

[1] 1e-08

print(gg+
geom_line(aes(x=log(h),y=log(rel_err_gf2)))+
ggtitle('Aproximación a la Hessiana por diferencias finitas'))

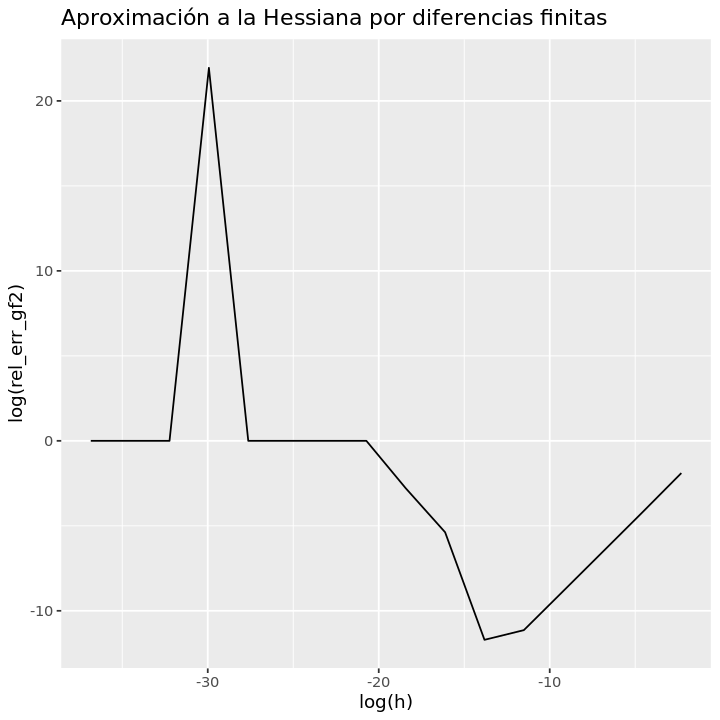
print(h[which.min(rel_err_gf2)])

[1] 1e-06

Ejercicio

Utilizando lenguajes de programación aproximar $\mathrm{\nabla }f(x),{\mathrm{\nabla }}^{2}f(x)$ con diferencias hacia delante y $h\in \{{10}^{-16},{10}^{-14},\dots ,{10}^{-1}\}$ para $f:{\mathbb{R}}^3\to \mathbb{R}$, dada por $f(x)=x_1{x}_2\exp (x_1^2+x_3^2-5)$ en el punto $x_0=(1,3,-2{)}^T$ Realizar una gráfica de $\log ($Err_rel) vs $\log ($h).

Ejercicios

1. Resuelve los ejercicios y preguntas de la nota.

Referencias

1. R. L. Burden, J. D. Faires, Numerical Analysis, Brooks/Cole Cengage Learning, 2005.

2. M. T. Heath, Scientific Computing. An Introductory Survey, McGraw-Hill, 2002.

3. S. P. Boyd, L. Vandenberghe, Convex Optimization. Cambridge University Press, 2004.