4.5 Método primal-dual de barrera logarítmica (BL)

Notas para contenedor de docker:

Comando de docker para ejecución de la nota de forma local:

nota: cambiar <ruta a mi directorio> por la ruta de directorio que se desea mapear a /datos dentro del contenedor de docker y <versión imagen de docker> por la versión más actualizada que se presenta en la documentación.

docker run --rm -v <ruta a mi directorio>:/datos --name jupyterlab_optimizacion_2 -p 8888:8888 -d palmoreck/jupyterlab_optimizacion_2:<versión imagen de docker>

password para jupyterlab: qwerty

Detener el contenedor de docker:

docker stop jupyterlab_optimizacion_2

Documentación de la imagen de docker palmoreck/jupyterlab_optimizacion_2:<versión imagen de docker> en liga.

---

Nota generada a partir de liga1, liga2, liga3

Al final de esta nota la comunidad lectora:

• Conocerá el método primal dual de barrera logarítmica para resolver programas lineales.

• Aprenderá que tal método:

  • es un caso particular de métodos de penalización para resolver problemas de optimización con restricciones.

  • tiene la capacidad de resolver problemas convexos.

  • trabaja con bloques de matrices lo que ayuda a aprovechar operaciones vectoriales o matriciales.

  • puede implementarse con cómputo en paralelo.

El método primal-dual de barrera logarítmica (BL) es un método iterativo que realiza un manejo de las variables primales y duales del problema de optimización a resolver. Se le clasifica como un método por puntos interiores.

Un poco de historia …

El método símplex desarrollado por Dantzig en los \(40\)’s hizo posible que se formularan y analizaran modelos en la categoría de large scale en una forma sistemática y eficiente. Hoy en día continúa siendo uno de los métodos más utilizados para resolver programas lineales. No obstante puede ser ineficiente en problemas lineales “patológicos” (ver Klee-Minty cube) pues el tiempo para resolver tales problemas es exponencial respecto al tamaño del problema (medido como el número de variables, de restricciones y la cantidad de almacenamiento para los datos del problema). Para la mayoría de problemas prácticos el método símplex es mucho más eficiente que estos casos “patológicos” pero esto motivó la investigación y desarrollo de nuevos algoritmos con mejor desempeño. En 1984 Karmarkar publicó el algoritmo que lleva su mismo nombre que tiene una complejidad polinomial y en la práctica resultó ser eficiente. Pertenece a la clase de métodos con el nombre de puntos interiores. Hay diferentes tipos de métodos por puntos interiores siendo los de la clase primal-dual ampliamente usados en la práctica.

Métodos por puntos interiores (PI)

Los métodos por puntos interiores (PI) son esquemas iterativos que en un inicio se utilizaron para resolver PL’s, sin embargo, se ha extendido su uso al caso no lineal. Por ejemplo, distintos tipos de métodos por PI han sido usados para resolver problemas de optimización convexos, ver problemas de optimización convexa en su forma estándar o canónica.

Recuérdese que nombramos problemas de optimización con restricciones large scale a aquellos problemas de optimización que tienen un número de variables y restricciones mayor o igual a \(10^5\) (ambas).

En cada iteración de los métodos PI las restricciones de desigualdad del problema de optimización se satisfacen de forma estricta. Cada iteración es costosa de calcular y realiza avance significativo a la solución en contraste con el método símplex que requiere un gran número de iteraciones no costosas. Una característica que tienen los métodos PI es que los problemas large scale no requieren muchas más iteraciones que los problemas small scale a diferencia del método símplex. Sin embargo para problemas small scale en general realizan más iteraciones que el método símplex.

En cada iteración el método símplex se mueve de la solución FEV actual a una solución FEV adyacente por una arista de la frontera de la región factible, ver método símplex. Los problemas del tipo large scale tienen una cantidad enorme de soluciones FEV. Para ver esto piénsese en un PL al que se le van añadiendo restricciones funcionales. Entonces se añadirán aristas y por tanto soluciones FEV. Los métodos PI evitan tal comportamiento pues avanzan por el interior de la región factible hacia los puntos óptimos y tiene muy poco efecto el ir añadiedo restricciones funcionales al PL para el desempeño de los métodos PI.

Observación

Los métodos PI han mostrado “buena” eficiencia (en términos del número de iteraciones realizadas) en resolver problemas de optimización large scale. Además son métodos que pueden implementarse para procesamiento con cómputo en paralelo.

Los métodos PI conforme avanzan en las iteraciones aproximan a los puntos óptimos en el límite. Por ejemplo, para el ejemplo prototipo de un programa lineal (PL) a continuación se presenta una trayectoria obtenida por un método PI que se aproxima a la solución óptima \((2, 6)\):

\[\displaystyle \max_{x \in \mathbb{R}^2} 3x_1 + 5x_2\]

\[\text{sujeto a: }\]

\[x_1 \leq 4\]

\[2x_2 \leq 12\]

\[3x_1 + 2x_2 \leq 18\]

\[x_1 \geq 0, x_2 \geq 0\]

import numpy as np
import matplotlib.pyplot as plt

np.set_printoptions(precision=3, suppress=True)

#x_1 ≤ 4

point1_x_1 = (4,0)

point2_x_1 = (4, 10)

point1_point2_x_1 = np.row_stack((point1_x_1, point2_x_1))

#x_1 ≥ 0
point3_x_1 = (0,0)

point4_x_1 = (0, 10)

point3_point4_x_1 = np.row_stack((point3_x_1, point4_x_1))

#2x_2 ≤ 12 or x_2 ≤ 6

point1_x_2 = (0, 6)

point2_x_2 = (8, 6)

point1_point2_x_2 = np.row_stack((point1_x_2, point2_x_2))

#x_2 ≥ 0

point3_x_2 = (0, 0)

point4_x_2 = (8, 0)

point3_point4_x_2 = np.row_stack((point3_x_2, point4_x_2))

#3x_1 + 2x_2 ≤ 18

x_1_region_1 = np.linspace(0,4, 100)

x_2_region_1 = 1/2*(18 - 3*x_1_region_1)


x_1 = np.linspace(0,6, 100)

x_2 = 1/2*(18 - 3*x_1)

plt.plot(point1_point2_x_1[:,0], point1_point2_x_1[:,1],
         point3_point4_x_1[:,0], point3_point4_x_1[:,1],
         point1_point2_x_2[:,0], point1_point2_x_2[:,1],
         point3_point4_x_2[:,0], point3_point4_x_2[:,1],
         x_1, x_2)

optimal_point = (2, 6)

plt.scatter(optimal_point[0], optimal_point[1], marker='o', s=150,
            facecolors="none", edgecolors='b')

plt.legend(["$x_1 = 4$", "$x_1 = 0$", 
            "$2x_2 = 12$", "$x_2 = 0$",
            "$3x_1+2x_2 = 18$", "(óptimo coordenada 1, óptimo coordenada 2)"], bbox_to_anchor=(1, 1))

point_1_interior_points = (1, 2)
point_2_interior_points = (1.27, 4)
point_3_interior_points = (1.38, 5)
point_4_interior_points = (1.56, 5.5)

points_interior_points = np.row_stack((point_1_interior_points,
                                       point_2_interior_points,
                                       point_3_interior_points,
                                       point_4_interior_points))

plt.plot(points_interior_points[:, 0], points_interior_points[:, 1], 
         marker='o', color="blue"
         )

plt.fill_between(x_1_region_1, 0, x_2_region_1, where=x_2_region_1<=6, color="plum")
x_1_region_2 = np.linspace(0,2, 100)
plt.fill_between(x_1_region_2, 0, 6, color="plum")
plt.title("Región factible del PL")
plt.show()

Recuérdese que los parámetros de un PL son \(b_i, c_i, a_{ij}\).

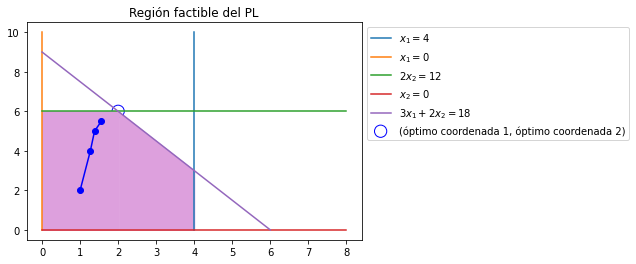
Aunque los métodos PI son una buena alternativa para resolver PL’s perdemos ventajas que tiene el método símplex como es el análisis de sensibilidad y el análisis posterior que puede realizarse al modificar los parámetros del PL. Ver las referencias al final de la nota para tales análisis.

Método primal-dual

Se describirán dos ideas que se utilizan en los métodos primal dual y posteriormente una tercera idea que utiliza la función de barrera logarítmica (FBL). Para esto, considérese la forma estándar de un PL (PLE):

\[\begin{split} \displaystyle \min_{x \in \mathbb{R}^n} c^Tx\\ \text{sujeto a:} \\ Ax=b\\ x \geq 0 \end{split}\]

donde: \(A \in \mathbb{R}^{m \times n}, b \in \mathbb{R}^m\), \(m < n\) con rank completo por renglones y las restricciones se interpretan de una forma pointwise.

Las restricciones \(Ax = b\) se pueden escribir con funciones \(h_i: \mathbb{R}^n \rightarrow \mathbb{R}\) , \(h_i(x) = b_i-a_i ^Tx\), \(a_i\) \(i\)-ésimo renglón de \(A \in \mathbb{R}^{m \times n}\) y \(b_i\) \(i\)-ésima entrada de \(b\) para \(i=1, \cdots, m\). Las restricciones \(x \geq 0\) se escriben con funciones \(f_i: \mathbb{R}^n \rightarrow \mathbb{R}\), \(f_i(x) = -x_i\) para \(i=1, \cdots, n\).

La función Lagrangiana del problema anterior es:

\[\mathcal{L}(x, \lambda, \nu) = f_o(x) + \displaystyle \sum_{i=1}^n \lambda_i f_i(x) + \sum_{i=1}^m \nu_i h_i(x) = c^Tx + \lambda^T(-x) + \nu^T(b-Ax)\]

donde: \(\mathcal{L}: \mathbb{R}^n \times \mathbb{R}^n \times \mathbb{R}^m \rightarrow \mathbb{R}\).

El problema dual asociado es:

El problema primal es:

\[\begin{split}\displaystyle \min_{x \in \mathbb{R}^n} c^Tx \\ \text{sujeto a:}\\ Ax = b \\ x \geq 0 \end{split}\]

\(A \in \mathbb{R}^{m \times n}\) y rank de A igual a \(m < n\).

\[\begin{split}\displaystyle \max_{\nu \in \mathbb{R}^m, \lambda \in \mathbb{R}^n} b^T \nu \\ \text{sujeto a :} \\ c - A^T \nu - \lambda = 0 \\ \lambda \geq 0 \end{split}\]

Las condiciones KKT son:

Ver las condiciones KKT para un PL en su forma estándar.

\[\begin{split} \begin{eqnarray} \nabla_x \mathcal{L}(x, \lambda, \nu) &=& c - A^T\nu - \lambda = 0 \nonumber \\ \lambda^Tx &=& 0 \nonumber \\ Ax &=& b \nonumber \\ -x &\leq& 0 \nonumber \\ \lambda &\geq& 0 \end{eqnarray} \end{split}\]

Los métodos de la clase primal-dual encuentran soluciones \((x^*, \lambda^*, \nu^*)\) para las igualdades anteriores y modifican las direcciones de búsqueda y tamaños de paso para que las desigualdades se satisfagan de forma estricta en cada iteración.

En los métodos de la clase primal-dual reescribimos las condiciones KKT de optimalidad anteriores mediante una función \(F: \mathbb{R}^{2n + m} \rightarrow \mathbb{R}^{2n+m}\) dada por:

\[\begin{split}F(x, \lambda, \nu ) = \left [ \begin{array}{c} c - A^T \nu - \lambda \\ X \Lambda e \\ b - Ax \end{array} \right ]\end{split}\]

El bloque \(X \Lambda e\) es una forma matricial de escribir \(\lambda ^T x\). Recuérdese que \(\lambda ^T x=0\) es una expresión que resume a la holgura complementaria \(\lambda_i x_i = 0\) \(\forall i=1, \cdots, n\) pues \(\lambda_i \geq 0, x_i \geq 0\).

y resolvemos la ecuación no lineal \(F(x, \lambda, \nu )=0\) para \((x, \lambda) \geq 0\), donde: \(X = \text{diag}(x_1, \dots, x_n)\), \(\Lambda = \text{diag}(\lambda_1, \dots, \lambda_n)\) y \(e\) es un vector de \(1\)’s en \(\mathbb{R}^n\). Además en cada iteración se cumple \(x^{(k)} > 0\) y \(\lambda^{(k)} > 0\) para \((x^{(k)}, \lambda^{(k)}, \nu^{(k)})\), por esto tales métodos son considerados como puntos interiores.

Como la mayoría de los métodos iterativos en optimización, los métodos primal-dual tienen un procedimiento para determinar la dirección de búsqueda y una cantidad que debe ser monitoreada cuyo valor alcance un valor objetivo. En el caso de los PLE’s tal cantidad es la duality gap medida como: \(\lambda^Tx\), ver brecha dual.

Primera idea: determinar la dirección de búsqueda

Sistema de ecuaciones no lineales a resolver:

\(F(x, \lambda, \nu ) = \left [ \begin{array}{c} c - A^T \nu - \lambda \\ X \Lambda e \\ b - Ax \end{array} \right ] = 0\)

La dirección de búsqueda se determina aplicando el método de Newton al sistema de ecuaciones no lineales que se muestra en el margen del PLE. Por tanto, se resuelve el sistema de ecuaciones lineales:

\[\begin{split}J_F(x, \lambda, \nu) \left [ \begin{array}{c} \Delta x \\ \Delta \lambda \\ \Delta \nu \end{array} \right ] = - F(x, \lambda, \nu)\end{split}\]

donde: \(J_F\) es la Jacobiana de \(F\) cuya expresión es:

\[\begin{split}J_F(x, \lambda, \nu) = \left [ \begin{array}{ccc} 0 & I & -A^T \\ \Lambda & X & 0 \\ -A & 0 & 0 \end{array} \right ].\end{split}\]

para el vector de incógnitas \(\left [ \begin{array}{c} \Delta x \\ \Delta \lambda \\ \Delta \nu \end{array} \right ]\).

Una vez calculado tal vector de incógnitas se realiza la actualización:

\[\begin{split}\left [ \begin{array}{c} x \\ \lambda \\ \nu \end{array} \right ]^{(k+1)} = \left [ \begin{array}{c} x \\ \lambda \\ \nu \end{array} \right ]^{(k)} + \left [ \begin{array}{c} \Delta x \\ \Delta \lambda \\ \Delta \nu \end{array} \right ]\end{split}\]

donde: \(k\) hace referencia a la \(k\)-ésima iteración.

Ver Sistema de ecuaciones no lineales.

Observación

Si bien podría elegirse otra dirección de búsqueda, la dirección de Newton (o variantes de ésta) se prefiere por sus propiedades de convergencia e invarianza ante transformaciones afín.

En el caso en el que la terna \((x, \lambda, \nu)\) no sea una terna primal-dual factible se utiliza \(r_d = c - A^T \nu - \lambda, r_p = b - Ax\) como el residual para factibilidad dual y residual para factibilidad primal respectivamente. Se busca en las iteraciones que sean tales residuales iguales o cercanos a cero. En este caso el sistema de ecuaciones lineales a resolver es:

\[\begin{split}\left [ \begin{array}{ccc} 0 & I & -A^T \\ \Lambda & X & 0 \\ -A & 0 & 0 \end{array} \right ] \left [ \begin{array}{c} \Delta x \\ \Delta \lambda \\ \Delta \nu \end{array} \right ] = - \left [ \begin{array}{c} r_d \\ X \Lambda e \\ r_p \end{array} \right ]\end{split}\]

Comentarios

• El sistema de ecuaciones lineales anterior para problemas large scale no se construye pues es un sistema cuadrado de tamaño \(2n + m \times 2n + m\) y se resuelve reduciéndolo a sistemas de ecuaciones equivalentes. Representa el paso más costoso del método primal-dual.

• Se pueden eliminar los signos negativos que están en los bloques de la matriz del sistema de ecuaciones lineales anterior que contienen \(A, A^T\) pero por consistencia con lo desarrollado en la nota de dualidad para un PL se mantienen los signos negativos (si se eliminan también debe de ajustarse el lado derecho del sistema). Esta modificación se relaciona con la definición de la función Lagrangiana.

• El método primal-dual se le nombra path following method para el caso en el que se tenga una terna no primal-dual factibles (se trabaja con los residuales primal y dual)

Segunda idea: cortar el paso

Si se toma un paso completo es muy posible que en la siguiente iteración se encuentre muy cerca de alguna de las fronteras de restricción o bien se salga de la región factible. Para esto se define un parámetro \(t^{(k)} \in (0, 1]\) y por tanto la actualización es:

\[\begin{split}\left [ \begin{array}{c} x \\ \lambda \\ \nu \end{array} \right ]^{(k+1)} = \left [ \begin{array}{c} x \\ \lambda \\ \nu \end{array} \right ]^{(k)} + t^{(k)} \left [ \begin{array}{c} \Delta x \\ \Delta \lambda \\ \Delta \nu \end{array} \right ]\end{split}\]

donde: \(k\) hace referencia a la \(k\)-ésima iteración.

Comentario

El parámetro \(t^{(k)}\) se calcula con metodologías como búsqueda de línea o regiones de confianza, ver line search, método de búsqueda de línea por backtracking, trust region.

Método primal-dual de barrera logarítmica (BL)

Tercera idea: reducir la duality gap y centrar. Uso de la función de barrera logarítmica (FBL)

En cada iteración los métodos primal-dual buscan reducir la duality gap o bien mantenerse “cerca” de la trayectoria nombrada trayectoria central.

Sistema de ecuaciones lineales \(\left [ \begin{array}{ccc} 0 & I & -A^T \\ \Lambda & X & 0 \\ -A & 0 & 0 \end{array} \right ] \left [ \begin{array}{c} \Delta x \\ \Delta \lambda \\ \Delta \nu \end{array} \right ] = - \left [ \begin{array}{c} r_d \\ X \Lambda e \\ r_p \end{array} \right ]\)

Comentario

Recuérdese que la duality gap en un PLE para el par \((x, \nu)\) primal-dual factible está dada por la diferencia: \(c^Tx - b^T \nu\). La duality gap en un PLE es igual a \(\lambda^Tx\). En el sistema de ecuaciones lineales que se muestra en el margen se representa cada sumando de \(\lambda^Tx\) con el producto \(X \Lambda e\) (recuérdese \(X, \Lambda\) son matrices diagonales).

La trayectoria central se define a partir de la FBL, ver Barrier function. La definición siguiente se da para un POCE de forma general.

Las restricciones \(Ax = b\) se pueden escribir con funciones \(h_i: \mathbb{R}^n \rightarrow \mathbb{R}\) , \(h_i(x) = b_i-a_i ^Tx\), \(a_i\) \(i\)-ésimo renglón de \(A \in \mathbb{R}^{p \times n}\) y \(b_i\) \(i\)-ésima entrada de \(b\) para \(i=1, \cdots, p\). Obsérvese el POCE y compárese con el PLE donde las restricciones \(x \geq 0\) se escriben con funciones \(f_i: \mathbb{R}^n \rightarrow \mathbb{R}\), \(f_i(x) = -x_i\) para \(i=1, \cdots, n\).

Definición

Considérese el problema de optimización convexa en la forma estándar (POCE):

\[\begin{split} \begin{eqnarray} \displaystyle \min_{x \in \mathbb{R}^n} &f_o(x)& \nonumber \\ &\text{sujeto a:}& \nonumber\\ f_i(x) &\leq& 0 \quad i=1,\dots,m \nonumber \\ Ax &=& b \end{eqnarray} \end{split}\]

con \(A \in \mathbb{R}^{p \times n}\) y rank de \(A\) igual a \(p < n\).

Se define la función de barrera logarítmica (FBL) como:

\[\phi(x) =-\displaystyle \sum_{i=1}^m \log(-f_i(x))\]

y \(\phi: \mathbb{R}^n \rightarrow \mathbb{R}\).

Un poco de historia …

La metodología para resolver el problema de barrera logarítmica (PBL) está fundamentada en la sequential unconstrained minimization technique (SUMT), A. V. Fiacco, G. P. McCormick, 1965. Es una técnica para resolver problemas no lineales sin restricciones que genera una secuencia de puntos interiores factibles que convergen a la solución del problema. Se eligen funciones de barrera con propiedades como la convexidad. Hay versiones de la SUMT para puntos exteriores que inician con puntos no factibles y vía la penalización se busca la convergencia hacia la región factible. En cada iteración de SUMT se define un valor del parámetro de barrera y se resuelve un problema de optimización más sencillo que el original con el método de Newton. La solución de tal problema se utiliza para definir puntos iniciales del siguiente problema a resolver con un valor del parámetro de barrera diferente. A medida que se avanza en las iteraciones la función objetivo del PBL se aproxima cada vez más a \(f_o\), al valor óptimo y al conjunto óptimo.

El POCE se resuelve planteando el siguiente problema:

\[\begin{split} \displaystyle \min_{x \in \mathbb{R}^n} f_B(x|t_B) \\ \text{sujeto a:} \\ Ax = b \end{split}\]

donde: \(f_B(x|t_B) = f_o(x) + \frac{1}{t_B} \phi(x) = f_o(x) - \frac{1}{t_B} \displaystyle \sum_{i=1}^m \log(-f_i(x))\) con \(t_B\) un parámetro positivo que nombramos parámetro de barrera. Denotamos a este problema como problema de barrera logarítmica (PBL).

A continuación se visualiza la FBL considerando un PLE con \(f_i(x) = -x_i\) para diferentes valores de \(t_B\).

x = np.linspace(-2, -.1, 100)
log_barrier = -np.log(-x)
t_B1 = 0.2
t_B2 = 0.5
t_B3 = 1
t_B4 = 2
t_B5 = 10
plt.plot(x, 1/t_B1*log_barrier, "r",
         x, 1/t_B2*log_barrier, "b",
         x, 1/t_B3*log_barrier, "g",
         x, 1/t_B4*log_barrier, "m",
         x, 1/t_B5*log_barrier, "c")
plt.legend(["$t_{B1}=0.2$",
            "$t_{B2}=0.5$",
            "$t_{B3}=1$",
            "$t_{B4}=2$",
            "$t_{B5}=10$"], bbox_to_anchor=(1,1))
plt.axhline(color="black")
plt.axvline(color="black")
plt.title("Gráfica de la FBL variando el parámetro $t_B$")
plt.show()

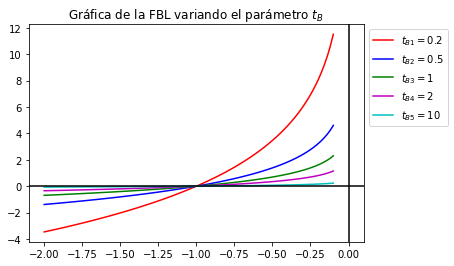
Valores más grandes de \(t_B\) hacen que \(f_B(x|t_B)\) tienda a \(f_o(x)\):

\[f_B(x|t_B) = f_o(x) + \frac{1}{t_B} \phi(x) \approx f_o(x).\]

El POCE recuérdese es:

\( \begin{eqnarray} \displaystyle \min_{x \in \mathbb{R}^n} &f_o(x)& \nonumber \\ &\text{sujeto a:}& \nonumber\\ f_i(x) &\leq& 0 \quad i=1,\dots,m \nonumber \\ Ax &=& b \end{eqnarray} \)

y el PBL es:

\[\begin{split} \displaystyle \min_{x \in \mathbb{R}^n} f_B(x|t_B) \\ \text{sujeto a:} \\ Ax = b \end{split}\]

con \(A \in \mathbb{R}^{p \times n}\) y rank de \(A\) igual a \(p < n\),

\(\begin{eqnarray} f_B(x|t_B) &=& f_o(x) + \frac{1}{t_B} \phi(x) \nonumber \\ &=& f_o(x) - \frac{1}{t_B} \displaystyle \sum_{i=1}^m \log(-f_i(x)) \end{eqnarray} \)

Comentarios

• En un PLE podemos definir \(f:\mathbb{R}^n \rightarrow \mathbb{R}\) con \(f(x) = -x\) (cada entrada de \(f\) es \(f_i(x) = -x_i\)) y la función \(\phi(x)\) queda como \(\phi(x) = -\frac{1}{t_B} f(x) = -\frac{1}{t_B} \log(-x)\) para \(x < 0\) es convexa, diferenciable. La FBL \(\phi(x)\) aproxima a la función indicadora:

\[\begin{split}I(x) = \begin{cases} \infty \text{ si } x > 0 \\ 0 \text{ si } x \leq 0 \end{cases}\end{split}\]

la cual es una función discontinua:

En el dibujo anterior sólo se visualiza para el eje horizontal el intervalo \((-\infty, 0)\).

• La función indicadora del punto anterior ayuda a reescribir el POCE como:

\[\displaystyle \min_{x \in \mathbb{R}^n} f_o(x) + \displaystyle \sum_{i=1}^m I(f_i(x))\]

\[\text{sujeto a:}\]

\[Ax = b\]

por esto resolver el PBL es equivalente a resolver el POCE para valores más grandes de \(t_B\).

• La FBL es un caso particular de funciones de barrera que penalizan al no satisfacer las restricciones de desigualdad, ver Penalty method.

• En general las funciones de barrera deben tener las siguientes propiedades para \(x\) primal factibles:

1. Tener valores “pequeños” si \(x\) está “lejos” de la frontera de la región factible.

2. Tener valores “grandes” si \(x\) está “cerca” de la frontera de la región factible.

3. Tener propiedades como convexidad o diferenciabilidad (ventajas al tener tales propiedades).

Por lo anterior las funciones de barrera evitan que se cruce o llegue a la frontera de la región factible del problema primal.

• Otra función de barrera para un PL es: \(\phi(x) = -\displaystyle \sum_{i=1}^m \frac{1}{f_i(x)}\) para \(x\) factibles.

• Los problemas de optimización convexos con únicamente restricciones de igualdad pueden resolverse aplicando extensiones del método de Newton.

Trayectoria central determinada por los puntos centrales

Definición

Para cada valor del parámetro de barrera \(t_B\), se definen los puntos centrales \(x^*(t_B)\) como la solución del PBL y el conjunto de puntos centrales se le nombra trayectoria central, central path.

Revisemos las condiciones KKT de optimalidad que deben cumplir los puntos centrales para un PLE:

\[\begin{split} \displaystyle \min_{x \in \mathbb{R}^n} c^Tx\\ \text{sujeto a:} \\ Ax=b\\ x \geq 0 \end{split}\]

con \(A \in \mathbb{R}^{m \times n}\) y rank de \(A\) igual a \(m < n\).

Se tiene:

Recuérdese que en un PLE \(f_i(x) = - x_i \forall i=1, \cdots, n\).

\[\begin{split} \begin{eqnarray} \phi(x) &=& -\displaystyle \sum_{i=1}^n \log(-f_i(x)) \nonumber \\ &=& - \sum_{i=1}^n \log(x_i) \end{eqnarray} \end{split}\]

y por tanto el PBL para el PLE (PBL-PLE) es:

El PBL para un POCE recuérdese es:

\[\begin{split} \displaystyle \min_{x \in \mathbb{R}^n} f_B(x|t_B) \\ \text{sujeto a:} \\ Ax = b \end{split}\]

con \(A \in \mathbb{R}^{p \times n}\) y rank de \(A\) igual a \(p < n\),

\(\begin{eqnarray} f_B(x|t_B) &=& f_o(x) + \frac{1}{t_B} \phi(x) \nonumber \\ &=& f_o(x) - \frac{1}{t_B} \displaystyle \sum_{i=1}^m \log(-f_i(x)) \end{eqnarray} \)

\[\displaystyle \min_{x \in \mathbb{R}^n} c^Tx - \frac{1}{t_B} \displaystyle \sum_{i=1}^n \log(x_i)\]

\[\text{sujeto a:}\]

\[Ax=b\]

La función Lagrangiana del PBL-PLE es:

\[\begin{split} \begin{eqnarray} \mathcal{L}_B(x, \nu) &=& f_B(x|t_B) + \sum_{i=1}^m \nu_i h_i(x) \nonumber \\ &=& f_o(x) - \frac{1}{t_B} \displaystyle \sum_{i=1}^m \log(-f_i(x)) + \sum_{i=1}^m \nu_i h_i(x) \nonumber \\ &=& c^Tx - \frac{1}{t_B} \displaystyle \sum_{i=1}^n \log(x_i) + \sum_{i=1}^m \nu_i(b_i-a_i ^Tx) \nonumber \\ &=& c^Tx - \frac{1}{t_B} \displaystyle \sum_{i=1}^n \log(x_i) + \nu^T(b-Ax) \nonumber \end{eqnarray} \end{split}\]

con \(a_i\) \(i\)-ésimo renglón de \(A\) y \(b_i\) \(i\)-ésima entrada de \(b\). En esta última igualdad puede definirse \(h:\mathbb{R}^n \rightarrow \mathbb{R}^m\) como \(h(x) = b-Ax\). Las condiciones necesarias y suficientes KKT de optimalidad del PBL-PLE son:

Recuérdese que las condiciones de KKT para un PLE son:

\( \begin{eqnarray} \nabla_x \mathcal{L}(x, \lambda, \nu) &=& c - A^T\nu - \lambda = 0 \nonumber \\ \lambda^Tx &=& 0 \nonumber \\ Ax &=& b \nonumber \\ -x &\leq& 0 \nonumber \\ \lambda &\geq& 0 \end{eqnarray} \)

Ver condiciones KKT para un PL en su forma estándar

\[\begin{split} \begin{eqnarray} \nabla_x \mathcal{L}_B(x, \nu) &=& c - A^T\nu - \frac{1}{t_B}d = 0 \nonumber \\ Ax &=& b \nonumber \\ \end{eqnarray} \end{split}\]

donde: \(d = X^{-1}e = \left [ \begin{array}{c} \frac{1}{x_1} \\ \vdots \\ \frac{1}{x_n} \\ \end{array} \right ]\).

Definición

Los puntos centrales \(x^*(t_B)\) para un PBL-PLE satisfacen:

\[\begin{split} \begin{eqnarray} \nabla_x \mathcal{L}_B(x^*(t_B), \nu) &=& c - A^T\nu - \frac{1}{t_B} d(t_B) = 0 \nonumber \\ Ax^*(t_B) &=& b \nonumber \\ \end{eqnarray} \end{split}\]

donde: \(d(t_B) = X^{*-1}(t_B)e = \left [ \begin{array}{c} \frac{1}{x_1^*(t_B)} \\ \vdots \\ \frac{1}{x_n^*(t_B)} \\ \end{array} \right ]\).

Relación entre las condiciones KKT de optimalidad del PLE y las del PBL-PLE

Para establecer la relación entre las condiciones KKT de optimalidad del PLE y las del PBL-PLE considérese sólo en esta sección que el PBL-PLE es:

\[\displaystyle \min_{x \in \mathbb{R}^n} t_B c^Tx - \displaystyle \sum_{i=1}^n \log(x_i)\]

\[\text{sujeto a:}\]

\[Ax=b\]

La FBL en el PBL-PLE recuérdese es:

\( \begin{eqnarray} \phi(x) &=& -\displaystyle \sum_{i=1}^n \log(-f_i(x)) \nonumber \\ &=& - \sum_{i=1}^n \log(x_i) \end{eqnarray} \)

Observación

Esta forma del PBL-PLE es equivalente a la revisada anteriormente en la que la FBL se divide por el parámetro \(t_B\). Es una cuestión sólo de escritura matemática lo que se realiza a continuación.

Las condiciones KKT son iguales a las revisadas en la sección anterior salvo la posición en la que se tiene el parámetro \(t_B\):

\[\begin{split} \begin{eqnarray} \nabla_x \mathcal{L}_B(x^*(t_B), \hat{\nu}) &=& t_Bc - A^T\hat{\nu} - d(t_B) = 0 \nonumber \\ Ax^*(t_B) &=& b \nonumber \\ \end{eqnarray} \end{split}\]

donde: \(\hat{\nu} = t_B \nu\).

Recuérdese que las condiciones de KKT para un PLE son:

\( \begin{eqnarray} \nabla_x \mathcal{L}(x, \lambda, \nu) &=& c - A^T\nu - \lambda = 0 \nonumber \\ \lambda^Tx &=& 0 \nonumber \\ Ax &=& b \nonumber \\ -x &\leq& 0 \nonumber \\ \lambda &\geq& 0 \end{eqnarray} \)

Las condiciones KKT para un PLE se muestran en el margen y obsérvese que si \(\lambda_i^*(t_B) = - \frac{1}{t_B f_i(x^*(t_B))} = - \frac{1}{t_B (-x_i^*(t_B))}\) con \(x_i^*(t_B)\) \(i\)-ésima componente de \(x^*(t_B)\) \(\forall i = 1, \dots, n\) entonces se cumple:

\[\lambda_i^*(t_B) > 0\]

pues por la definición de la FBL en el PBL-PLE debe cumplirse: \(f_i(x) = -x_i < 0\) o bien para los puntos centrales \(-x_i^*(t_B) < 0 \forall i=1, \dots, n\). Lo anterior se garantiza por el dominio de la función \(\log\) la cual está definida únicamente en \(\mathbb{R}_{++}\) (reales positivos). Esto satisface las desigualdades de factibilidad primal y de factibilidad dual de las condiciones KKT de optimalidad.

Recuérdese que la holgura complementaria en un PLE es: \(\lambda_i x_i = 0 \forall i=1, \dots,n\) y como \(\lambda_i \geq 0, x_i \geq 0\) se reescribe como \(\lambda ^T x = 0\).

El producto \(\lambda^Tx\) que se tiene en la holgura complementaria, para las condiciones KKT de optimalidad en un PBL-PLE son:

\[\begin{split} \begin{eqnarray} \lambda^*(t_B)^Tx^*(t_B) &=& \displaystyle \sum_{i=1}^n \lambda_i^*(t_B) x_i^*(t_B) \nonumber \\ &=& \displaystyle \sum_{i=1}^n - \frac{x_i^*(t_B)}{t_B (-x_i^*(t_B))} \nonumber \\ &=& \displaystyle \sum_{i=1}^n \frac{1}{t_B} = \frac{n}{t_B} \end{eqnarray} \end{split}\]

El POCE recuérdese es:

\( \begin{eqnarray} \displaystyle \min_{x \in \mathbb{R}^n} &f_o(x)& \nonumber \\ &\text{sujeto a:}& \nonumber\\ f_i(x) &\leq& 0 \quad i=1,\dots,m \nonumber \\ Ax &=& b \end{eqnarray} \)

y el PBL es:

\[\begin{split} \displaystyle \min_{x \in \mathbb{R}^n} f_B(x|t_B) \\ \text{sujeto a:} \\ Ax = b \end{split}\]

con \(A \in \mathbb{R}^{p \times n}\) y rank de \(A\) igual a \(p < n\),

\(\begin{eqnarray} f_B(x|t_B) &=& f_o(x) + \frac{1}{t_B} \phi(x) \nonumber \\ &=& f_o(x) - \frac{1}{t_B} \displaystyle \sum_{i=1}^m \log(-f_i(x)) \end{eqnarray} \)

Por tanto la duality gap asociada con \(x^*(t_B), \lambda^*(t_B), \nu^*(t_B)\) es: \(\frac{n}{t_B}\) donde: \(\nu^*(t_B) = \frac{\hat{\nu}}{t_B}\).

Recuérdese que las condiciones de KKT para un PLE son:

\( \begin{eqnarray} \nabla_x \mathcal{L}(x, \lambda, \nu) &=& c - A^T\nu - \lambda = 0 \nonumber \\ \lambda^Tx &=& 0 \nonumber \\ Ax &=& b \nonumber \\ -x &\leq& 0 \nonumber \\ \lambda &\geq& 0 \end{eqnarray} \)

Comentarios

• Por la forma de la duality gap anterior para los puntos centrales si \(t_B\) se incrementa entonces la duality gap tiende a cero en el método primal dual de BL.

• Para un PBL que se obtiene de un POCE la duality gap anterior para los puntos centrales es \(\frac{m}{t_B}\) pues se tienen \(m\) funciones \(f_i\) de desigualdad.

• Las condiciones KKT de optimalidad del PBL-PLE son las condiciones KKT de optimalidad del PLE (que se muestran en el margen) pero perturbadas por el parámetro \(t_B\):

\[\begin{split} \begin{eqnarray} \nabla_x \mathcal{L}_B(x(t_B), \hat{\nu}) &=& t_Bc - A^T\hat{\nu} - d(t_B) = 0 \nonumber \\ Ax(t_B) &=& b \nonumber \\ \lambda_i(t_B)x_i(t_B) &=& \frac{1}{t_B} \end{eqnarray} \end{split}\]

donde: \(\hat{\nu} = t_B \nu\), \(d(t_B) = X^{-1}(t)e = \left [ \begin{array}{c} \frac{1}{x_1(t_B)} \\ \vdots \\ \frac{1}{x_n(t_B)} \\ \end{array} \right ]\) y la duality gap se estima como: \(\lambda(t_B)^Tx(t_B) = \frac{n}{t_B}\).

¿Cómo calcular los puntos centrales?

Para calcular los puntos centrales del PBL-PLE se utiliza la primera idea: determinar la dirección de búsqueda en la que se resuelve el siguiente sistema de ecuaciones no lineales con el método de Newton:

El PBL-PLE recuérdese es:

\[\begin{split} \displaystyle \min_{x \in \mathbb{R}^n} c^Tx - \frac{1}{t_B} \displaystyle \sum_{i=1}^n \log(x_i) \nonumber \\ \text{sujeto a:} \nonumber \\ Ax=b \end{split}\]

con \(A \in \mathbb{R}^{m \times n}\) y rank de \(A\) igual a \(m < n\). Las condiciones KKT son:

\( \begin{eqnarray} \nabla_x \mathcal{L}_B(x, \nu) &=& c - A^T\nu - \frac{1}{t_B}d = 0 \nonumber \\ Ax &=& b \nonumber \\ \end{eqnarray} \)

donde: \(d = X^{-1}e = \left [ \begin{array}{c} \frac{1}{x_1} \\ \vdots \\ \frac{1}{x_n} \\ \end{array} \right ]\)

\[\begin{split}F(x, \nu) = \left [ \begin{array}{c} c - A^T\nu - \frac{1}{t_B}d(t_B) \\ b- Ax(t_B) \end{array} \right ] = 0\end{split}\]

donde: \(d(t_B) = X^{*-1}(t)e = \left [ \begin{array}{c} \frac{1}{x_1^*(t_B)} \\ \vdots \\ \frac{1}{x_n^*(t_B)} \\ \end{array} \right ]\).

Este sistema de ecuaciones no lineales conduce a resolver el sistema de ecuaciones lineales:

\[\begin{split}J_F(x, \nu) \left [ \begin{array}{c} \Delta x \\ \Delta \nu \end{array} \right ] = - F(x, \nu)\end{split}\]

donde: \(J_F(x, \nu) = \left [ \begin{array}{cc} \nabla_{xx} ^2 \mathcal{L}_B(x, \nu) & \nabla_{\nu x} \mathcal{L}_B(x,\nu) \\ -A & 0\end{array} \right ] = \left [ \begin{array}{cc} \frac{1}{t_B} D^2(t_B) & -A^T \\ -A & 0\end{array} \right ]\) y \(D^2(t_B) = \text{diag}^2(d(t_B)) \in \mathbb{R}^{n \times n}\).

La actualización en el método de Newton es:

\[\begin{split}\left [ \begin{array}{c} x \\ \nu \end{array} \right ]^{(k+1)} = \left [ \begin{array}{c} x \\ \nu \end{array} \right ]^{(k)} + t^{(k)} \left [ \begin{array}{c} \Delta x \\ \Delta \nu \end{array} \right ]\end{split}\]

donde se utilizó la segunda idea: cortar el paso.

Comentarios

• Se pueden eliminar los signos negativos que están en los bloques de la matriz del sistema de ecuaciones lineales anterior que contienen \(A, A^T\) pero por consistencia con lo desarrollado en la nota de dualidad para un PL se mantienen los signos negativos (si se eliminan también debe de ajustarse el lado derecho del sistema). Esta modificación se relaciona con la definición de la función Lagrangiana.

• También una modificación que se realiza para que en el primer bloque del sistema de ecuaciones lineales anterior no tengamos del lado izquierdo y del lado derecho \(\frac{1}{t_B}\) se puede trabajar con el problema de optimización equivalente:

\[\begin{split} \displaystyle \min_{x \in \mathbb{R}^n} f_B(x|t_B) \\ \text{sujeto a:} \\ Ax = b \end{split}\]

donde: \(f_B(x|t_B) = t_Bf_o(x) + \phi(x) = t_Bf_o(x) - \displaystyle \sum_{i=1}^m \log(-f_i(x))\).

Estas dos modificaciones se utilizan para implementar el método primal-dual de BL.

Método primal-dual de BL aplicado al ejemplo prototipo

!pip install --quiet "git+https://github.com/ITAM-DS/analisis-numerico-computo-cientifico.git#egg=opt&subdirectory=src"

Se utiliza el paquete de Python opt con los siguientes import’s.

from opt.utils_logarithmic_barrier import constraints_inequalities_funcs_generator, \
constraints_inequalities_funcs_eval

El problema de optimización para mostrar el uso del método primal dual de BL será el del ejemplo prototipo el cual sólo involucra restricciones de desigualdad.

\[\begin{split} \displaystyle \max_{x \in \mathbb{R}^2} 3x_1 + 5x_2\\ \text{sujeto a: } \\ x_1 \leq 4 \nonumber \\ 2x_2 \leq 12 \\ 3x_1 + 2x_2 \leq 18 \\ x_1 \geq 0 \\ x_2 \geq 0 \\ \end{split}\]

Reescribimos el problema anterior sin las restricciones \(A x \leq b\) y \(x \geq 0\) definiendo la función \(\phi: \mathbb{R}^n \rightarrow \mathbb{R}\) como \(\phi(x) = - \displaystyle \sum_{i=1}^m \log(-(a_i ^Tx-b_i)) - \sum_{i=1}^n \log(-{e}_i ^T(-x))\) con \(a_i\) \(i\)-ésimo renglón de \(A = \left [ \begin{array}{cc} 1 & 0 \\0 & 2 \\ 3 & 2 \end{array} \right ]\), \(b_i\) \(i\)-ésima entrada del vector \(b = \left [ \begin{array}{c} 4 \\ 12 \\ 18 \end{array} \right ]\) y \(e_i\) \(i\)-ésimo vector canónico.

Por tanto, el PBL tomando como función objetivo la FBL \(t_Bf_o(x) + \phi(x)\) queda como sigue:

\[\begin{split} \displaystyle \min_{x \in \mathbb{R}^2} t_B(-3x_1 -5x_2) - [\log(4-x_1) + \log(12 - 2x_2) + \log(18 - (3 x_1 + 2 x_2)) + \log(x_1) + \log(x_2) ]\\ \end{split}\]

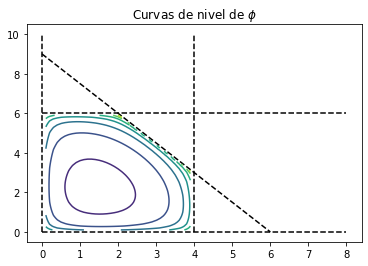
Para este problema las curvas de nivel de la función \(\phi\) se ven como sigue:

const_ineq_two_pars = {0: lambda x1,x2: x1 - 4,
                       1: lambda x1,x2: 2*x2 - 12,
                       2: lambda x1,x2: 3*x1 + 2*x2 - 18,
                       3: lambda x1,x2: -x1,
                       4: lambda x1,x2: -x2
                       }
def const_ineq_funcs_eval_two_pars(x1,x2, 
                                   const_ineq):
    """
    Auxiliary function for the evaluation of constraint inequalities
    in logarithmic barrier function using two parameters as input.
    """
    const_ineq_funcs_eval = np.array([const(x1,x2) for const in \
                                      constraints_inequalities_funcs_generator(const_ineq)])
    return const_ineq_funcs_eval
def phi_two_pars(x1,x2, const_ineq):
    """
    Implementation of phi function for logarithmic barrier using two 
    parameters as input.
    """
    const_ineq_funcs_eval = -const_ineq_funcs_eval_two_pars(x1,
                                                            x2,
                                                            const_ineq)
    log_barrier_const_eval = np.log(const_ineq_funcs_eval)
    return -np.sum(log_barrier_const_eval, axis=0)

density=1e-1
x1l=0.1
x2d=0.1
x1r=4
x2u=8
x1_p=np.arange(x1l,x1r,density)
x2_p=np.arange(x2d,x2u,density)
x1_mesh,x2_mesh = np.meshgrid(x1_p,x2_p)
z = phi_two_pars(x1_mesh,x2_mesh,const_ineq_two_pars)
plt.plot(point1_point2_x_1[:,0], point1_point2_x_1[:,1], "--", color="black", label="_nolegend_") 
plt.plot(point3_point4_x_1[:,0], point3_point4_x_1[:,1], "--", color="black", label="_nolegend_")
plt.plot(point1_point2_x_2[:,0], point1_point2_x_2[:,1], "--", color="black", label="_nolegend_")
plt.plot(point3_point4_x_2[:,0], point3_point4_x_2[:,1], "--", color="black", label="_nolegend_")
plt.plot(x_1, x_2, "--", color="black", label="_nolegend_")
plt.contour(x1_p, x2_p, z)
plt.title("Curvas de nivel de $\phi$")

plt.show()

/tmp/ipykernel_73/215958759.py:24: RuntimeWarning: divide by zero encountered in log
  log_barrier_const_eval = np.log(const_ineq_funcs_eval)
/tmp/ipykernel_73/215958759.py:24: RuntimeWarning: invalid value encountered in log
  log_barrier_const_eval = np.log(const_ineq_funcs_eval)

Realizamos la actualización:

\[\begin{split}\left [ \begin{array}{c}x_1 \\ x_2 \end{array} \right ] = \left [ \begin{array}{c}x_1 \\ x_2 \end{array} \right ] + t \left [ \begin{array}{c}\Delta x_1 \\ \Delta x_2 \end{array} \right ]\end{split}\]

donde: \(t\) es parámetro de backtracking y \(\left [ \begin{array}{c}\Delta x_1 \\ \Delta x_2 \end{array} \right ]\) es solución del sistema de ecuaciones lineales:

\[\begin{split} \nabla^2f_{B}(x) \left [ \begin{array}{c}\Delta x_1 \\ \Delta x_2 \end{array} \right ] = - \nabla f_{B}(x) \nonumber \\ \end{split}\]

que para este problema es:

\[\begin{split} \begin{eqnarray} \tilde{A}^T \text{diag}^2(d(t_B))\tilde{A} \left [ \begin{array}{c}\Delta x_1 \\ \Delta x_2 \end{array} \right ] &=& -(t_Bc + \tilde{A}^Td(t_B)) \nonumber \end{eqnarray} \end{split}\]

donde:

\(c = \left [ \begin{array}{c}-3 \\ -5 \end{array} \right ], \tilde{A} = \left [ \begin{array}{c} A \\ I \end{array} \right ] = \left [ \begin{array}{cc} 1 & 0 \\0 & 2 \\ 3 & 2 \\ 1 & 0 \\ 0 & 1 \end{array} \right ]\), \(b_i\) \(i\)-ésima entrada del vector \(b = \left [ \begin{array}{c} 4 \\ 12 \\ 18 \end{array} \right ]\).

Y el vector \(d(t_B) = \left [ \begin{array}{c} \frac{1}{b_1 - a_1^Tx(t_B)} \\ \frac{1}{b_2 - a_2^Tx(t_B)} \\ \frac{1}{b_3 - a_3^Tx(t_B)} \\ \frac{1}{-x_1(t_B)} \\ \frac{1}{-x_2(t_B)} \end{array}\right ] = \left [ \begin{array}{c} \frac{1}{4-x_1(t_B)} \\ \frac{1}{12-2x_2(t_B)} \\ \frac{1}{18-3x_1(t_B)-2x_2(t_B)} \\ \frac{1}{-x_1(t_B)} \\ \frac{1}{-x_2(t_B)} \end{array}\right ]\).

Observación

Aunque podríamos definir las siguientes líneas de acuerdo al desarrollo matemático anterior:

A = np.array([[1, 0],
              [0, 2],
              [3, 2]])
m = 3
n = 2
b = np.array([4, 12, 18])
A_tilde = np.row_stack((A, np.eye(n)))

d = np.array([1/(b[0]-A[0,:].dot(x)),
              1/(b[1]-A[1,:].dot(x)),
              1/(b[2]-A[2,:].dot(x)),
              1/(-x[0]),
              1/(-x[1])])
system_matrix = (A_tilde.T*(d*d))@A_tilde
rhs = -(t_B*c +A_tilde.T@d)

usamos SymPy para uso de diferenciación simbólica (no se recomienda el uso de SymPy para problemas medium o large scale).

Comentario

Valores más “grandes” de \(t_B\) hacen que la Hessiana de la función objetivo del PBL varíe rápidamente cerca de la frontera del conjunto factible. En este ejemplo prototipo algunas de las entradas de \(\text{diag}^2(d(t_B))\) serán muy grandes en tales valores de \(t_B\).

import sympy
from sympy.tensor.array import derive_by_array

from opt.compute_step_size import line_search_by_backtracking
from opt.classes.functions import LogarithmicBarrier, GradientLogarithmicBarrier, \
HessianLogarithmicBarrier

def map_sympy_vars_to_array_values(x):
    """
    Auxiliary function to evaluate derivatives of sympy which are defined
    in terms of symbols x1, x2.
    Args:
        x (numpy ndarray): 1d array of floats
    Returns:
        dictionary of the form {x1: x[0], x2: x[1],...} to map sympy Symbols
        to values.
    """
    n = x.size
    return {"x%s" % i: x[i-1] for i in range(1,n+1)}

c = np.array([-3, -5])
b = np.array([4, 12, 18], dtype=float)
x_0 = np.array([1, 2], dtype=float)
n = x_0.size
#sympy definitions
x1, x2 = sympy.symbols("x1, x2")
x_sympy = (x1, x2)
fo_sympy = c[0]*x1 + c[1]*x2
phi_sympy = -(sympy.log(b[0]-x1) + sympy.log(b[1]-2*x2) + sympy.log(b[2]-3*x1-2*x2) + sympy.log(x1) + sympy.log(x2))
gf_sympy = derive_by_array(fo_sympy, x_sympy)
Hf_sympy = derive_by_array(gf_sympy, x_sympy)
gphi_sympy = derive_by_array(phi_sympy, x_sympy)
Hphi_sympy = derive_by_array(gphi_sympy,x_sympy)
gf = lambda x: np.array([first_partial_derivative.subs(map_sympy_vars_to_array_values(x)) \
                         for first_partial_derivative in gf_sympy],
                         dtype = float)

gphi = lambda x: np.array([first_partial_derivative.subs(map_sympy_vars_to_array_values(x)) \
                           for first_partial_derivative in gphi_sympy],
                           dtype = float)

Hf = lambda x: np.array([second_partial_derivative.subs(map_sympy_vars_to_array_values(x)) \
                         for second_partial_derivative in Hf_sympy],
                                dtype=float).reshape(n,n)

Hphi = lambda x: np.array([second_partial_derivative.subs(map_sympy_vars_to_array_values(x)) \
                           for second_partial_derivative in Hphi_sympy],
                                dtype=float).reshape(n,n)

gf_class = GradientLogarithmicBarrier(gf, gphi)
Hf_class = HessianLogarithmicBarrier(Hf, Hphi)

Primera iteración

#constraints inequalities definition as < = 0

constraints_ineq = {0: lambda x: x[0] - b[0],
                    1: lambda x: 2*x[1] - b[1],
                    2: lambda x: 3*x[0] + 2*x[1] - b[2],
                    3: lambda x: -x[0],
                    4: lambda x: -x[1]
                   }

#definition of objective function with numpy

fo_numpy = lambda x: np.dot(c, x)

#parameter for logarithmic barrier method
t_B_0 = 10

log_barrier_class = LogarithmicBarrier(fo_numpy,
                                       constraints_ineq)
log_barrier_class.set_x(x_0)
log_barrier_class.set_t_B(t_B_0)
log_barrier_class.evaluate()
log_barrier_eval = log_barrier_class.logarithmic_barrier_eval

Aquí evaluamos la función objetivo del PBL del ejemplo prototipo:

\(\begin{eqnarray} f_B(x|t_B) &=& t_B(-3x_1 -5x_2) \nonumber \\ &-& \log(4-x_1) - \log(12 - 2x_2) \nonumber \\ &-& \log(18 - (3 x_1 + 2 x_2)) \nonumber \\ &-& \log(x_1) - \log(x_2) \end{eqnarray} \)

print(log_barrier_eval)

-136.26909628370626

const_ineq_funcs_eval = -constraints_inequalities_funcs_eval(x_0,constraints_ineq)

print(const_ineq_funcs_eval)

[ 3.  8. 11.  1.  2.]

Aquí revisamos que al evaluar las restricciones esté dentro del dominio de la función \(\log\) (valores estrictamente positivos). Si no están los puntos en el dominio debemos devolver un mensaje y detener el método.

if(sum(const_ineq_funcs_eval < -np.nextafter(0,1)) >=1):
    print("Some constraint inequalities evaluated in x were nonpositive, check approximations")

fo_eval = log_barrier_class.f_eval

print(fo_eval)

-13.0

Hf_class.set_x(x_0)
Hf_class.set_t_B(t_B_0)
Hf_class_eval = Hf_class.evaluate()
system_matrix = Hf_class_eval
gf_class.set_x(x_0)
gf_class.set_t_B(t_B_0)
gf_class_eval = gf_class.evaluate()
rhs = -gf_class_eval

Resolvemos el sistema de ecuaciones lineales para calcular la dirección de Newton.

dir_Newton = np.linalg.solve(system_matrix, rhs)

print(dir_Newton)

[ 19.696 142.065]

Aquí calculamos el decremento de Newton cuya definición se da al finalizar las iteraciones.

dec_Newton_squared = rhs.dot(dir_Newton)

print(dec_Newton_squared)

7711.552360817478

stopping_criteria = dec_Newton_squared/2

print(stopping_criteria)

3855.776180408739

der_direct = -dec_Newton_squared

Aquí cortamos el paso con la metodología de búsqueda de línea por backtracking.

t = line_search_by_backtracking(log_barrier_class,
                                dir_Newton,
                                der_direct)

/home/myuser/.local/lib/python3.8/site-packages/opt/utils_logarithmic_barrier.py:17: RuntimeWarning: invalid value encountered in log
  eval_f_const_inequality = np.log(eval_f_const_inequality)

print(t)

0.015625

x = x_0 + t*dir_Newton

print(x)

[1.308 4.22 ]

Segunda iteración

log_barrier_class.set_x(x)
log_barrier_class.evaluate()
log_barrier_eval = log_barrier_class.logarithmic_barrier_eval

print(log_barrier_eval)

-255.9181764898568

const_ineq_funcs_eval = -constraints_inequalities_funcs_eval(x,constraints_ineq)

print(const_ineq_funcs_eval)

[2.692 3.56  5.637 1.308 4.22 ]

if(sum(const_ineq_funcs_eval < -np.nextafter(0,1)) >=1):
    print("Some constraint inequalities evaluated in x were nonpositive, check approximations")

fo_eval = log_barrier_class.f_eval

print(fo_eval)

-25.0220423713883

Hf_class.set_x(x)
Hf_class.set_t_B(t_B_0)
Hf_class_eval = Hf_class.evaluate()
system_matrix = Hf_class_eval
gf_class.set_x(x)
gf_class.set_t_B(t_B_0)
gf_class_eval = gf_class.evaluate()
rhs = -gf_class_eval

dir_Newton = np.linalg.solve(system_matrix, rhs)

print(dir_Newton)

[11.93  94.597]

dec_Newton_squared = rhs.dot(dir_Newton)

print(dec_Newton_squared)

5021.819828077724

stopping_criteria = dec_Newton_squared/2

print(stopping_criteria)

2510.909914038862

der_direct = -dec_Newton_squared

t = line_search_by_backtracking(log_barrier_class,
                                dir_Newton,
                                der_direct)

print(t)

0.015625

x = x + t*dir_Newton

print(x)

[1.494 5.698]

Tercera iteración

log_barrier_class.set_x(x)
log_barrier_class.evaluate()
log_barrier_eval = log_barrier_class.logarithmic_barrier_eval

print(log_barrier_eval)

-333.0255657565843

const_ineq_funcs_eval = -constraints_inequalities_funcs_eval(x,constraints_ineq)

print(const_ineq_funcs_eval)

[2.506 0.604 2.122 1.494 5.698]

if(sum(const_ineq_funcs_eval < -np.nextafter(0,1)) >=1):
    print("Some constraint inequalities evaluated in x were nonpositive, check approximations")

fo_eval = log_barrier_class.f_eval

print(fo_eval)

-32.97166508298113

Hf_class.set_x(x)
Hf_class.set_t_B(t_B_0)
Hf_class_eval = Hf_class.evaluate()
system_matrix = Hf_class_eval
gf_class.set_x(x)
gf_class.set_t_B(t_B_0)
gf_class_eval = gf_class.evaluate()
rhs = -gf_class_eval

dir_Newton = np.linalg.solve(system_matrix, rhs)

print(dir_Newton)

[9.648 2.785]

dec_Newton_squared = rhs.dot(dir_Newton)

print(dec_Newton_squared)

406.31377617547037

stopping_criteria = dec_Newton_squared/2

print(stopping_criteria)

203.15688808773518

der_direct = -dec_Newton_squared

t = line_search_by_backtracking(log_barrier_class,
                                dir_Newton,
                                der_direct)

print(t)

0.03125

x = x + t*dir_Newton

print(x)

[1.796 5.785]

Ejercicio

Utiliza las definiciones:

A = np.array([[1, 0],
              [0, 2],
              [3, 2]])
m = 3
n = 2
b = np.array([4, 12, 18])
A_tilde = np.row_stack((A, np.eye(n)))

d = np.array([1/(b[0]-A[0,:].dot(x)),
              1/(b[1]-A[1,:].dot(x)),
              1/(b[2]-A[2,:].dot(x)),
              1/(-x[0]),
              1/(-x[1])])
system_matrix = (A_tilde.T*(d*d))@A_tilde
rhs = -(t_B*c +A_tilde.T@d)

y realiza cuatro iteraciones recalculando lo necesario para el sistema de ecuaciones lineales con system_matrix y rhs dadas por las últimas dos líneas del código que está en este ejercicio. Corrobora que obtienes los mismos resultados que con SymPy.

El POCE recuérdese es:

\( \begin{eqnarray} \displaystyle \min_{x \in \mathbb{R}^n} &f_o(x)& \nonumber \\ &\text{sujeto a:}& \nonumber\\ f_i(x) &\leq& 0 \quad i=1,\dots,m \nonumber \\ Ax &=& b \end{eqnarray} \)

y el PBL es:

\[\begin{split} \displaystyle \min_{x \in \mathbb{R}^n} f_B(x|t_B) \\ \text{sujeto a:} \\ Ax = b \end{split}\]

con \(A \in \mathbb{R}^{p \times n}\) y rank de \(A\) igual a \(p < n\),

\(\begin{eqnarray} f_B(x|t_B) &=& f_o(x) + \frac{1}{t_B} \phi(x) \nonumber \\ &=& f_o(x) - \frac{1}{t_B} \displaystyle \sum_{i=1}^m \log(-f_i(x)) \end{eqnarray} \)

Comentarios

• La forma general de la condición de KKT de optimalidad \(\nabla_x \mathcal{L}_B(x^, \nu) = 0\) para un PBL que se obtuvo de un POCE es:

\[\begin{split} \begin{eqnarray} \nabla_x \mathcal{L}_B(x, \nu) &=& \nabla f_o(x) + \frac{1}{t_B}\nabla \phi(x) + A^T \nu = 0 \nonumber \\ &=& \nabla f_o(x) + \frac{1}{t_B} \displaystyle \sum_{i=1}^m \frac{\nabla f_i(x)}{-f_i(x)} + A^T \nu \nonumber \\ \end{eqnarray} \end{split}\]

con: \(\mathcal{L}: \mathbb{R}^n \times \mathbb{R}^p \rightarrow \mathbb{R}\),

\[\begin{split}\begin{eqnarray} \mathcal{L}_B(x, \nu) &=& f_{B}(x|t_B) + \sum_{i=1}^p \nu_i h_i(x) \nonumber \\ &=& f_o(x|t_B) + \frac{1}{t_B} \phi(x) + \nu^T(b-Ax) \end{eqnarray} \end{split}\]

y al aplicar el método de Newton al sistema de ecuaciones no lineales conduce a resolver el sistema de ecuaciones lineales siguiente:

\[\begin{split}\left [ \begin{array}{cc} \nabla^2f_o(x) + \frac{1}{t_B} \nabla^2 \phi(x) & -A^T \\ -A & 0\end{array} \right ] \left [ \begin{array}{c} \Delta x \\ \Delta \nu \end{array} \right ] = -\left [ \begin{array}{c} \nabla f_o(x) + \frac{1}{t_B} \nabla \phi(x) \\ r_p \end{array} \right ]\end{split}\]

donde: \(r_p = b - Ax\) es el residual para factibilidad primal.

Ver la función Lagrangiana.

Definición decremento de Newton

Para problemas de optimización convexos sin restricciones:

\[\min_{x \in \mathbb{R}^n} f_o(x)\]

en los que utilizamos el método de Newton para resolverlos, se utiliza una cantidad en criterios de paro y en resultados de convergencia nombrada el decremento de Newton.

Definición

El decremento de Newton para \(f_o: \mathbb{R}^n \rightarrow \mathbb{R}\) en \(x\) es la cantidad:

\[\lambda(x) = (\nabla f_o(x)^T \nabla^2f_o(x)^{-1} \nabla f_o(x))^{1/2}\]

en donde se asume que \(f_o \in \mathcal{C}^2(\text{dom}f_o)\) y su Hessiana es definida positiva.

Observación

Obsérvese que si \(\nabla^2 f_o(x) = I\) entonces \(\lambda(x) = ||\nabla f_o(x)||_2\) por lo que el decremento de Newton generaliza el criterio de paro del monitoreo del gradiente de \(f_o\).

Comentarios

• Asumiendo que existe un punto óptimo \(x^*\) y el valor óptimo se denota por \(p^* = f_o(x^*)\) el decremento de Newton tiene propiedades como son:

  • \(\frac{1}{2} \lambda ^2 (x)\) estima \(f_o(x)-p^*\), por lo que tal cantidad se utiliza en las inner iterations del método primal-dual para resolver un PBL como criterio de paro.

  • \(|| \nabla^2 f_o(x)^{-1} \nabla f_o(x)||_{\nabla ^2f_o(x)} = \left ( \nabla f_o(x)^T \nabla^2 f_o(x)^{-1} \nabla ^2 f(x) \nabla ^2 f_o(x)^{-1} \nabla f_o(x) \right )^{1/2} = \lambda(x) \) que indica que \(\lambda(x)\) es la norma del paso de Newton bajo la norma cuadrática definida por la Hessiana de \(f_o\).

  • En el método de búsqueda de línea por backtracking, se utiliza \(-\lambda (x) ^2\) para calcular la derivada direccional de \(f_o\) en \(x\) en la dirección de \(\Delta x_{\text{nt}}\), lo cual se verifica en la siguiente línea:

\[\frac{df(x+t \Delta x_{\text{nt}})}{dt} \Bigr|_{t=0} = \nabla f_o(x)^T \Delta x_{\text{nt}} = \nabla f_o(x)^T (-\nabla^2 f_o(x)^{-1} \nabla f_o(x)) = -\lambda(x)^2\]

donde: \(t\) es el parámetro de búsqueda de línea por backtracking y \(\Delta x_{\text{nt}} = -\nabla ^2 f_o(x)^{-1} \nabla f_o(x)\) para \(x \in \text{dom}f_o\) es la dirección de Newton para \(f_o\) en \(x\). Ver Método de búsqueda de línea por backtracking.

Algoritmo primal-dual de BL para un PL con únicamente desigualdades

Para un problema de la forma:

\[\displaystyle \min_{x \in \mathbb{R}^n} c^Tx\]

\[\text{sujeto a:}\]

\[Ax \leq b\]

\[x \geq 0\]

Dados \(x\) un punto estrictamente factible, esto es: \(x > 0\), \(Ax < b\) (todas las entradas de \(x\) son positivas y \(a_i^Tx < b_i\)), \(t_B^{(0)}\) parámetro de barrera, \(\mu > 1\), \(tol > 0\).

\(t_B:= t_B^{(0)}\).

Repetir el siguiente bloque para \(k=1,2,\dots\)

Outer iterations:

Paso de centrado o inner iterations:

Calcular \(x^*(t_B)\) que resuelva: \(\displaystyle \min_{x \in \mathbb{R}^n} t_Bf_o(x) + \phi(x)\) iniciando con \(x\).

Utilizar criterio de paro para inner iterations.

Actualizar \(x:=x^*(t_B)\).

Incrementar \(t_B\) por \(t_B=\mu t_B\).

hasta convergencia: satisfacer criterio de paro en el que se utiliza \(tol\) y \(maxiter\).

Observación

Para un PL únicamente con desigualdades recuérdese:

\[t_Bf_o(x) + \phi(x) = t_B c^Tx - \displaystyle \sum_{i=1}^m \log(-(a_i ^Tx-b_i)) - \sum_{i=1}^n \log(-{e}_i ^T(-x))\]

con \(a_i\) \(i\)-ésimo renglón de \(A\).

Comentarios

• \(\mu\) es un parámetro que realiza un trade-off en el número de inner y outer iterations. Controla el seguimiento de la trayectoria central en las inner iterations. Valores grandes causan un mayor número de inner iterations y valores cercanos a \(1\) causan un mayor número de outer iterations.

• La elección de \(t_B^{(0)}\) ayuda a dar una estimación del recíproco de la duality gap (recuérdese que la estimación en un PBL-PLE es \(\frac{n}{t_B}\)). Es similar el efecto que con el parámetro \(\mu\). Valores grandes causan que se realicen mayor número de inner iterations y valores pequeños un mayor número de outer iterations.

• El criterio de paro de las outer iterations en un PBL-PLE es de la forma:

while n/t_B > tol && iterations < max_iters

y el de las inner iterations es de la forma:

while dec_Newton^2/2 > tol && iterations < max_iters

con dec_Newton^2/2 el decremento de Newton al cuadrado dividido por 2, tol una cantidad pequeña y positiva (comúnmente menor o igual a 10−8), iterations un contador de iteraciones.

• El algoritmo también puede regresar estimaciones para \(\lambda\) con \(\lambda^*(t_B)\) y \(\nu\) dada por \(\nu^*(t_B)\).

Método primal-dual de BL aplicado al ejemplo prototipo (completo)

Problema de optimización con únicamente desigualdades:

\[\begin{split} \displaystyle \max_{x \in \mathbb{R}^2} 3x_1 + 5x_2\\ \text{sujeto a: } \\ x_1 \leq 4 \nonumber \\ 2x_2 \leq 12 \\ 3x_1 + 2x_2 \leq 18 \\ x_1 \geq 0 \\ x_2 \geq 0 \\ \end{split}\]

Aquí nuevamente se definen variables que ya habían sido definidas y sólo se realiza esto para conocer cómo llamar a las diferentes clases, funciones y métodos del paquete opt.

from opt.classes.problems import ProblemFeasibleInitPoint

c = np.array([-3, -5])
b = np.array([4, 12, 18], dtype=float)
x_0 = np.array([1, 2], dtype=float)
n = x_0.size
#sympy definitions
x1, x2 = sympy.symbols("x1, x2")
x_sympy = (x1, x2)
fo_sympy = c[0]*x1 + c[1]*x2
phi_sympy = -(sympy.log(b[0]-x1) + sympy.log(b[1]-2*x2) + sympy.log(b[2]-3*x1-2*x2) + sympy.log(x1) + sympy.log(x2))
gf_sympy = derive_by_array(fo_sympy, x_sympy)
Hf_sympy = derive_by_array(gf_sympy, x_sympy)
gphi_sympy = derive_by_array(phi_sympy, x_sympy)
Hphi_sympy = derive_by_array(gphi_sympy,x_sympy)
gf = lambda x: np.array([first_partial_derivative.subs(map_sympy_vars_to_array_values(x)) \
                         for first_partial_derivative in gf_sympy],
                         dtype = float)

gphi = lambda x: np.array([first_partial_derivative.subs(map_sympy_vars_to_array_values(x)) \
                           for first_partial_derivative in gphi_sympy],
                           dtype = float)

Hf = lambda x: np.array([second_partial_derivative.subs(map_sympy_vars_to_array_values(x)) \
                         for second_partial_derivative in Hf_sympy],
                                dtype=float).reshape(n,n)

Hphi = lambda x: np.array([second_partial_derivative.subs(map_sympy_vars_to_array_values(x)) \
                           for second_partial_derivative in Hphi_sympy],
                                dtype=float).reshape(n,n)

gf_class = GradientLogarithmicBarrier(gf, gphi)
Hf_class = HessianLogarithmicBarrier(Hf, Hphi)

#constraints inequalities definition as < = 0

constraints_ineq = {0: lambda x: x[0] - b[0],
                    1: lambda x: 2*x[1] - b[1],
                    2: lambda x: 3*x[0] + 2*x[1] - b[2],
                    3: lambda x: -x[0],
                    4: lambda x: -x[1]
                   }

#definition of objective function with numpy

fo_numpy = lambda x: np.dot(c, x)

#parameters for logarithmic barrier method
mu = 10
t_B_0 = 10

#solution
x_ast = np.array([2, 6], dtype=float)
p_ast = fo_numpy(x_ast) 

type_problem = "CICO" #Constrained Inequality Convex Optimization
p = ProblemFeasibleInitPoint(type_problem, 
                             fo_numpy,
                             mu=mu,
                             constraints_ineq=constraints_ineq)

if p.well_defined_problem:
    print("problema %s bien definido" % p.type_problem)
else:
    print("problema %s no bien definido" % p.type_problem)

problema CICO bien definido

[x,total_iter,t_B,x_plot] = p.solve(x_0,
                                    t_B_0,
                                    x_ast=x_ast,
                                    p_ast=p_ast,
                                    gf_B=gf_class,
                                    Hf_B=Hf_class
                                   )

Outer iterations of primal-dual LB method
Mu value: 1.00e+01

	Outer iter	logbarrier	t_log_barrier	duality gap
row0	0	-1.36e+02	10	5.00e-01

-----------------------------------------------------------------
-----------------------------------------------------------------

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row0	0	5.86e+01	7.71e+03	6.52e-01	6.39e-01	---	3.47e+00

/home/myuser/.local/lib/python3.8/site-packages/opt/utils_logarithmic_barrier.py:17: RuntimeWarning: invalid value encountered in log
  eval_f_const_inequality = np.log(eval_f_const_inequality)

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row1	1	5.77e+01	5.02e+03	3.02e-01	3.05e-01	1.56e-02	2.46e+00

/home/myuser/.local/lib/python3.8/site-packages/opt/utils_logarithmic_barrier.py:17: RuntimeWarning: invalid value encountered in log
  eval_f_const_inequality = np.log(eval_f_const_inequality)

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row2	2	5.42e+01	4.06e+02	9.32e-02	8.41e-02	1.56e-02	4.99e+00

/home/myuser/.local/lib/python3.8/site-packages/opt/utils_logarithmic_barrier.py:17: RuntimeWarning: invalid value encountered in log
  eval_f_const_inequality = np.log(eval_f_const_inequality)

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row3	3	5.14e+01	1.17e+02	4.69e-02	4.69e-02	3.12e-02	3.79e+00

/home/myuser/.local/lib/python3.8/site-packages/opt/utils_logarithmic_barrier.py:17: RuntimeWarning: invalid value encountered in log
  eval_f_const_inequality = np.log(eval_f_const_inequality)

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row4	4	4.51e+01	2.27e+01	2.39e-02	2.42e-02	6.25e-02	3.51e+00

/home/myuser/.local/lib/python3.8/site-packages/opt/utils_logarithmic_barrier.py:17: RuntimeWarning: invalid value encountered in log
  eval_f_const_inequality = np.log(eval_f_const_inequality)

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row5	5	3.39e+01	2.35e-01	4.36e-03	3.81e-03	2.50e-01	5.96e+00

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row6	6	9.93e+00	4.36e-02	5.15e-03	4.89e-03	1	4.43e+00

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row7	7	1.63e+00	1.83e-03	5.46e-03	5.42e-03	1	3.80e+00

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row8	8	6.61e-02	3.35e-06	5.53e-03	5.53e-03	1	3.70e+00

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row9	9	1.21e-04	1.12e-11	5.53e-03	5.54e-03	1	3.69e+00

Error of x with respect to x_ast: 5.53e-03
Approximate solution: [1.989 5.967]

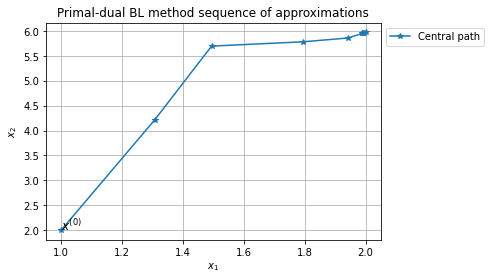
Inner iterations
[1.989 5.967]
-----------------------------------------------------------------
-----------------------------------------------------------------
Outer iterations of primal-dual LB method
Mu value: 1.00e+01

	Outer iter	logbarrier	t_log_barrier	duality gap
row1	1	-3.58e+03	100	5.00e-02

-----------------------------------------------------------------
-----------------------------------------------------------------

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row0	0	5.25e+02	1.61e+02	5.53e-03	5.54e-03	---	3.69e+00

/home/myuser/.local/lib/python3.8/site-packages/opt/utils_logarithmic_barrier.py:17: RuntimeWarning: invalid value encountered in log
  eval_f_const_inequality = np.log(eval_f_const_inequality)

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row1	1	4.50e+02	2.28e+01	2.43e-03	2.43e-03	6.25e-02	3.71e+00

/home/myuser/.local/lib/python3.8/site-packages/opt/utils_logarithmic_barrier.py:17: RuntimeWarning: invalid value encountered in log
  eval_f_const_inequality = np.log(eval_f_const_inequality)

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row2	2	2.75e+02	2.06e-01	3.76e-04	3.77e-04	2.50e-01	3.68e+00

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row3	3	6.68e+01	2.12e-02	4.98e-04	4.98e-04	1	3.69e+00

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row4	4	6.23e+00	2.26e-04	5.49e-04	5.50e-04	1	3.70e+00

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row5	5	6.54e-02	2.58e-08	5.55e-04	5.55e-04	1	3.70e+00

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row6	6	7.40e-06	3.42e-16	5.55e-04	5.55e-04	1	3.70e+00

Error of x with respect to x_ast: 5.55e-04
Approximate solution: [1.999 5.997]

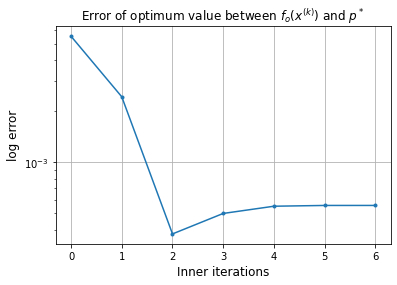
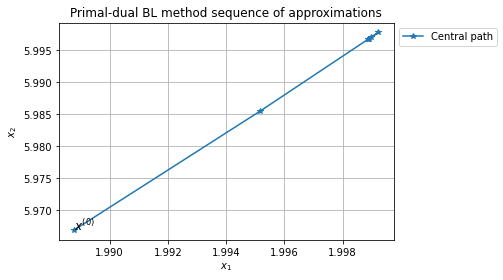
Inner iterations
[1.999 5.997]
-----------------------------------------------------------------
-----------------------------------------------------------------
Outer iterations of primal-dual LB method
Mu value: 1.00e+01

	Outer iter	logbarrier	t_log_barrier	duality gap
row2	2	-3.60e+04	1000	5.00e-03

-----------------------------------------------------------------
-----------------------------------------------------------------

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row0	0	5.25e+03	1.62e+02	5.55e-04	5.55e-04	---	3.70e+00

/home/myuser/.local/lib/python3.8/site-packages/opt/utils_logarithmic_barrier.py:17: RuntimeWarning: invalid value encountered in log
  eval_f_const_inequality = np.log(eval_f_const_inequality)

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row1	1	4.50e+03	2.28e+01	2.43e-04	2.43e-04	6.25e-02	3.71e+00

/home/myuser/.local/lib/python3.8/site-packages/opt/utils_logarithmic_barrier.py:17: RuntimeWarning: invalid value encountered in log
  eval_f_const_inequality = np.log(eval_f_const_inequality)

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row2	2	2.70e+03	2.01e-01	3.79e-05	3.80e-05	2.50e-01	3.70e+00

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row3	3	6.50e+02	2.02e-02	5.00e-05	5.00e-05	1	3.70e+00

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row4	4	5.93e+01	2.03e-04	5.50e-05	5.50e-05	1	3.71e+00

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row5	5	5.92e-01	2.06e-08	5.55e-05	5.55e-05	1	3.71e+00

	Iter	Normgf_B	Newtons decrement	Err x ast	Err p ast	line search	CondHf_B
row6	6	6.00e-05	2.13e-16	5.56e-05	5.56e-05	1	3.71e+00

Error of x with respect to x_ast: 5.56e-05
Approximate solution: [2. 6.]

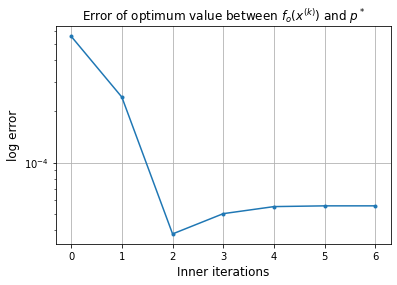
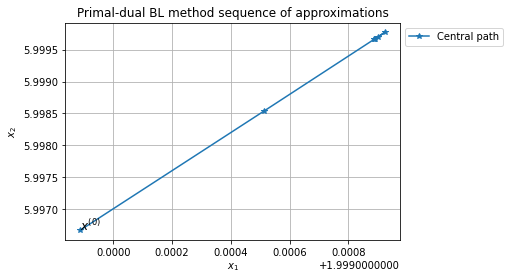
Inner iterations
[2. 6.]
-----------------------------------------------------------------
-----------------------------------------------------------------
Outer iterations of primal-dual LB method
Mu value: 1.00e+01

	Outer iter	logbarrier	t_log_barrier	duality gap
row3	3	-3.60e+05	10000	5.00e-04

-----------------------------------------------------------------
-----------------------------------------------------------------

Observación

Obsérvese que se realizan más iteraciones con el método primal-dual para este ejemplo prototipo que con el método símplex.

from opt.utils import plot_sequence_of_approximations

plt.contour(x1_p, x2_p, z)
plt.xlim(-0.1, 5)
plt.ylim(-0.1,6.5)

#level curves for fo
x_1_line_1 = np.linspace(0, 6, 100)
x_2_line_1 = 1/5*(-3*x_1_line_1 + 23)
x_1_line_2 = np.linspace(0, 6, 100)
x_2_line_2 = 1/5*(-3*x_1_line_2 + 29)
x_1_line_3 = np.linspace(0, 6, 100)
x_2_line_3 = 1/5*(-3*x_1_line_3 + 36)

plt.plot(x_1_line_1, x_2_line_1, "green",label="_nolegend_")
plt.plot(x_1_line_2, x_2_line_2, "indigo",label="_nolegend_")
plt.plot(x_1_line_3, x_2_line_3, "darkturquoise", label="_nolegend_")


#central path
plot_sequence_of_approximations(x_plot,
                                title="Primal-dual BL method sequence of approximations")

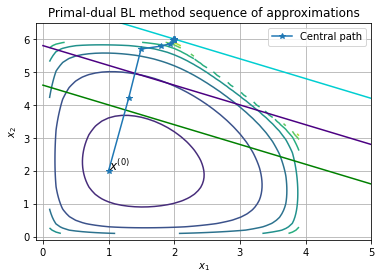
Comentario

En este ejemplo las curvas de nivel de la función objetivo \(f_o\) representadas con rectas en la gráfica anterior son tangentes a las curvas de nivel de \(\phi\) en \(x^*(t_B)\) pues: \(t_B \nabla f_o(x^*(t_B)) + \nabla \phi(x^*(t_B)) = 0\) por lo que:

\[\nabla \phi(x^*(t_B)) = -t_B \nabla f_o(x^*(t_B)) = -t_Bc\]

Ejercicio

Resolver el siguiente problema con el método primal-dual de BL y corrobora con algún software tu respuesta:

\[\begin{split} \displaystyle \min_{x \in \mathbb{R}^2} x_1 + x_2 - 4x_3\\ \text{sujeto a:} \\ x_1 + x_2 + 2x_3 \leq 9 \nonumber \\ x_1 + x_2 - x_3 \leq 2 \nonumber \\ -x_1 + x_2 + x_3 \leq 4 \nonumber \\ x_1 \geq 0, x_2 \geq 0, x_3 \geq 0 \end{split}\]

Ejercicios

1.Resuelve los ejercicios y preguntas de la nota.

Preguntas de comprehensión

1)¿Qué es un método por puntos interiores?

2)¿Qué se busca con el método primal-dual y cuáles son las ideas que se utilizan para su desarrollo?

3)¿Por qué al método primal-dual se le nombra así?

4)¿Qué efecto y ventajas tienen añadir funciones de barrera que penalizan al no satisfacer las restricciones de desigualdad de un problema de optimización?

5)¿Qué propiedades se buscan que satisfagan las funciones de barrera?

6)¿Por qué se elige el método de Newton para resolver el problema PBL?

7)¿Qué son los puntos centrales y la trayectoria central?

8)¿Qué relación existe entre las condiciones KKT de optimalidad del PLE y las del PBL-PLE (tu respuesta debe incluir la parametrización que se realiza en las condiciones para el PBL-PLE)?

9)¿Qué cantidad se monitorea en el método primal dual de barrera logarítmica que nos permite aproximar a la holgura complementaria, cuál es su expresión para el caso de un PLE y cómo se estima en el PBL-PLE?

10)¿Cómo se define y qué propiedades tiene el decremento de Newton?

11)Explica la tarea que tienen los parámetros \(\mu\) y \(t_B\) en el problema PBL. Puedes apoyar tu respuesta considerando el efecto que resulta de elegir valores grandes, pequeños de tales parámetros.

Referencias:

1. S. P. Boyd, L. Vandenberghe, Convex Optimization, Cambridge University Press, 2009.

2. J. Nocedal, S. J. Wright, Numerical Optimization, Springer, 2006.

3. F. Hillier, G. Lieberman, Introduction to Operations Research, Mc Graw Hill, 2014.