1.4 Condición de un problema y estabilidad de un algoritmo
Contents
1.4 Condición de un problema y estabilidad de un algoritmo#
Notas para contenedor de docker:
Comando de docker para ejecución de la nota de forma local:
nota: cambiar <ruta a mi directorio> por la ruta de directorio que se desea mapear a /datos dentro del contenedor de docker y <versión imagen de docker> por la versión más actualizada que se presenta en la documentación.
docker run --rm -v <ruta a mi directorio>:/datos --name jupyterlab_optimizacion -p 8888:8888 -d palmoreck/jupyterlab_optimizacion:<versión imagen de docker>
password para jupyterlab: qwerty
Detener el contenedor de docker:
docker stop jupyterlab_optimizacion
Documentación de la imagen de docker palmoreck/jupyterlab_optimizacion:<versión imagen de docker> en liga.
Nota generada a partir de liga
Al final de esta nota la comunidad lectora:
Podrá dar una justificación del por qué un algoritmo es exacto o inexacto en el cálculo de aproximaciones para cantidades de interés.
Aprenderá sobre los conceptos de condición de un problema y estabilidad de un algoritmo.
Comprenderá que el condicionamiento de un problema es inherente al problema mismo y no depende del algoritmo utilizado.
En específico se trabajará sobre el número de condición de una matriz como una cantidad que ayuda a clasificar problemas bien y mal condicionados en la solución de sistemas de ecuaciones lineales y otros.
Dos temas fundamentales en el análisis numérico son: la condición de un problema y estabilidad de un algoritmo. El condicionamiento tiene que ver con el comportamiento de un problema ante perturbaciones y la estabilidad con el comportamiento de un algoritmo (usado para resolver un problema) ante perturbaciones.
La exactitud de un cálculo dependerá finalmente de una combinación de estos términos:
Exactitud = Condición + Estabilidad
La falta de exactitud en un problema se presenta entonces por problemas mal condicionados (no importando si los algoritmos son estables o inestables) y algoritmos inestables (no importando si los problemas son mal o bien condicionados).
Perturbaciones#
La condición de un problema y estabilidad de un algoritmo hacen referencia al término perturbación. Tal término conduce a pensar en perturbaciones “chicas” o “grandes”. Para dar una medida de lo anterior se utiliza el concepto de norma. Ver Normas vectoriales y matriciales para definición de norma y propiedades.
Condición de un problema#
Pensemos a un problema como una función \(f: \mathbb{X} \rightarrow \mathbb{Y}\) con dato \(x \in \mathbb{X}\), donde: \(\mathbb{X}\) es un espacio vectorial de datos con norma definida y \(\mathbb{Y}\) es otro espacio vectorial de soluciones con una norma definida. Llamemos instancia de un problema a la combinación entre \(x,f\) y nos interesa el comportamiento de \(f\) en \(x\). Usamos el nombre de “problema” para referirnos al de instancia del problema.
Un problema (instancia) bien condicionado tiene la propiedad de que todas las perturbaciones pequeñas en \(x\) conducen a pequeños cambios en \(f(x)\). Y es mal condicionado si perturbaciones pequeñas en \(x\) conducen a grandes cambios en \(f(x)\). El uso de los términos “pequeño” o “grande” dependen del problema mismo.
Sea \(\hat{x} = x + \Delta x\) con \(\Delta x\) una perturbación pequeña de \(x\).
El número de condición relativo del problema \(f\) en \(x\) es:
considerando \(x,f(x) \neq 0\).
Observación
Si \(f\) es una función diferenciable, podemos evaluar \(\text{Cond}_f^R\) con la derivada de \(f\), pues a primer orden (usando teorema de Taylor): \(f(\hat{x})-f(x) \approx J(x)\Delta x\) con igualdad para \(\Delta x \rightarrow 0\) y \(J\) la Jacobiana de \(f\) definida como una matriz con entradas: \((J(x))_{ij} = \frac{\partial f_i(x)}{\partial x_j}\). Por tanto, se tiene:
y \(||J(x)||\) es una norma matricial inducida por las normas en \(\mathbb{X}, \mathbb{Y}\). Ver Normas vectoriales y matriciales.
Comentario
En la práctica se considera a un problema bien condicionado si \(\text{Cond}_f^R\) es “pequeño”: menor a \(10\), medianamente condicionado si es de orden entre \(10^1\) y \(10^2\) y mal condicionado si es “grande”: mayor a \(10^3\).
Ejercicio
Calcular \(\text{Cond}_f^R\) de los siguientes problemas. Para \(x \in \mathbb{R}\) usa el valor absoluto y para \(x \in \mathbb{R}^n\) usa \(||x||_\infty\).
\(x \in \mathbb{R} - \{0\}\). Problema: realizar la operación \(\frac{x}{2}\).
\(x \geq 0\). Problema: calcular \(\sqrt{x}\).
\(x \approx \frac{\pi}{2}\). Problema: calcular \(\cos(x)\).
\(x \in \mathbb{R}^2\). Problema: calcular \(x_1-x_2\).
Comentarios
Las dificultades que pueden surgir al resolver un problema no siempre están relacionadas con una fórmula o un algoritmo mal diseñado sino con el problema en cuestión. En el ejercicio anterior, observamos que áun utilizando aritmética exacta, la solución del problema puede ser altamente sensible a perturbaciones a los datos de entrada. Por esto el número de condición relativo se define de acuerdo a perturbaciones en los datos de entrada y mide la perturbación en los datos de salida que se esperan:
Para un ejemplo de problema mal condicionado en el contexto de cálculo de raíces de un polinomio ver Wilkinson’s polynomial.
Estabilidad de un algoritmo#
Pensemos a un algoritmo \(\hat{f}\) como una función \(\hat{f}:\mathbb{X}\rightarrow \mathbb{Y}\) para resolver el problema \(f\) con entrada \(x \in \mathbb{X}\), donde: \(\mathbb{X}\) es un espacio vectorial de entradas con norma definida y \(\mathbb{Y}\) es otro espacio vectorial con una norma definida que contiene números en un SPF. Ver nota: Sistema de punto flotante.
La implementación del algoritmo \(\hat{f}\) en una máquina conduce a considerar:
Errores por redondeo:
Operaciones en un SPF, \(\mathcal{Fl}\). Por ejemplo para la suma:
Esto es, \(\hat{f}\) depende de \(x \in \mathbb{X}\) y \(\epsilon_{maq}\): representación de los números reales en una máquina y operaciones entre ellos o aritmética de máquina.
Al ejecutar \(\hat{f}\) obtenemos una colección de números en el SPF que pertenecen a \(\mathbb{Y}\): \(\hat{f}(x)\).
Debido a las diferencias entre un problema con cantidades continuas y una máquina que trabaja con cantidades discretas, los algoritmos numéricos no son exactos para cualquier elección de entrada \(x \in \mathbb{X}\). Esto es, los algoritmos no cumplen que la cantidad:
dependa únicamente de errores por redondeo al evaluar \(f\) \(\forall x \in \mathbb{X}\). En notación matemática:
con \(K > 0\) no se cumple en general.
La razón de lo anterior tiene que ver con cuestiones en la implementación de \(\hat{f}\) como el número de iteraciones, la representación de \(x\) en un SPF o el mal condicionamiento de \(f\). Así, a los algoritmos en el análisis numérico, se les pide una condición menos estricta que la anterior y más bien satisfagan lo que se conoce como estabilidad. Se dice que un algoritmo \(\hat{f}\) para un problema \(f\) es estable si:
para \(\hat{x} \in \mathbb{X}\) tal que \(\frac{||x-\hat{x}||}{||x||} \leq K_2\epsilon_{maq}, K_2>0\).
Esto es, \(\hat{f}\) resuelve un problema cercano para entradas cercanas (cercano en el sentido del \(\epsilon_{maq}\)) independientemente de la elección de \(x\).
Observación
Obsérvese que esta condición es más flexible y en general \(K_1, K_2\) dependen de las dimensiones de \(\mathbb{X}, \mathbb{Y}\).
Comentarios
Esta definición resulta apropiada para la mayoría de los problemas en el ánalisis numérico. Para otros problemas, por ejemplo en ecuaciones diferenciales, donde se tienen definiciones de sistemas dinámicos estables e inestables (cuyas definiciones no se deben confundir con las descritas para algoritmos), esta condición es muy estricta.
Tenemos algoritmos que satisfacen una condición más estricta y simple que la estabilidad: estabilidad hacia atrás.
Estabilidad hacia atrás#
Decimos que un algoritmo \(\hat{f}\) para el problema \(f\) es estable hacia atrás si:
con \(\hat{x} \in \mathbb{X}\) tal que \(\frac{||x-\hat{x}||}{||x||} \leq K\epsilon_{maq}, K>0\).
Esto es, el algoritmo \(\hat{f}\) da la solución exacta para entradas cercanas (cercano en el sentido de \(\epsilon_{maq}\)), independientemente de la elección de \(x\).
Ejemplo#
Para entender la estabilidad hacia atrás de un algoritmo, considérese el ejemplo siguiente.
Problema: evaluar \(f(x) = e^x\) en \(x=1\).
Resultado: \(f(1) = e^1 = 2.718281...\).
import math
x=1
print(math.exp(x))
2.718281828459045
Algoritmo: truncar la serie \(1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \dots\) a cuatro términos: \(\hat{f}(x) = 1 + x + \frac{x^2}{2} + \frac{x^3}{6}\).
Resultado del algoritmo: \(\hat{f}(1) = 2.\bar{6}\)
algoritmo = lambda x: 1 + x + x**2/2.0 + x**3/6.0
print(algoritmo(1))
2.6666666666666665
Pregunta: ¿Qué valor \(\hat{x} \in \mathbb{R}\) hace que el valor calculado por el algoritmo \(\hat{f}(1)\) sea igual a \(f(\hat{x})\)?
-> Solución:
Resolver la ecuación: \(e^{\hat{x}} = 2.\bar{6}\), esto es: \(\hat{x} = log(2.\bar{6}) = 0.980829...\). Entonces \(f(\hat{x}) = 2.\bar{6} = \hat{f}(x)\).
x_hat = math.log(algoritmo(1))
print(x_hat)
0.9808292530117262
Entonces, el algoritmo es estable hacia atrás sólo si la diferencia entre \(x\) y \(\hat{x}\) en términos relativos es menor a \(K \epsilon_{maq}\) con \(K >0\). Además, podemos calcular errores hacia delante y errores hacia atrás (no relativos):
error hacia delante: \(\hat{f}(x) - f(x) = -0.05161...\), error hacia atrás: \(\hat{x}-x = -0.01917...\).
forward_error = algoritmo(x) - math.exp(x)
print(forward_error)
-0.05161516179237857
backward_error = x_hat-x
print(backward_error)
-0.019170746988273812
Dependiendo del problema, estos errores son pequeños o grandes, por ejemplo si consideramos tener una cifra correcta como suficiente para determinar que es una buena aproximación entonces podemos concluir: \(\hat{f}\) obtiene una respuesta correcta y cercana al valor de \(f\) (error hacia delante) y la respuesta que obtuvimos con \(\hat{f}\) es correcta para entradas ligeramente perturbadas (error hacia atrás).
Observaciones
Obsérvese que el error hacia delante requiere trabajar en \(\mathbb{Y}\) para resolver el problema \(f\) (cálculo de \(f(x)\)) y también información sobre \(f\). El error hacia atrás requiere trabajar en \(\mathbb{X}\) que en ocasiones es más simple que trabajar en \(\mathbb{Y}\).
En el ejemplo anterior se calcularon \(\hat{f}(x)\) y también qué tan larga debe ser la modificación en las entradas \(x\), esto es: \(\hat{x}\), para que \(\hat{f}(x) = f(\hat{x})\) (error hacia atrás).
Dibujo que ayuda a ver errores hacia atrás y hacia delante:
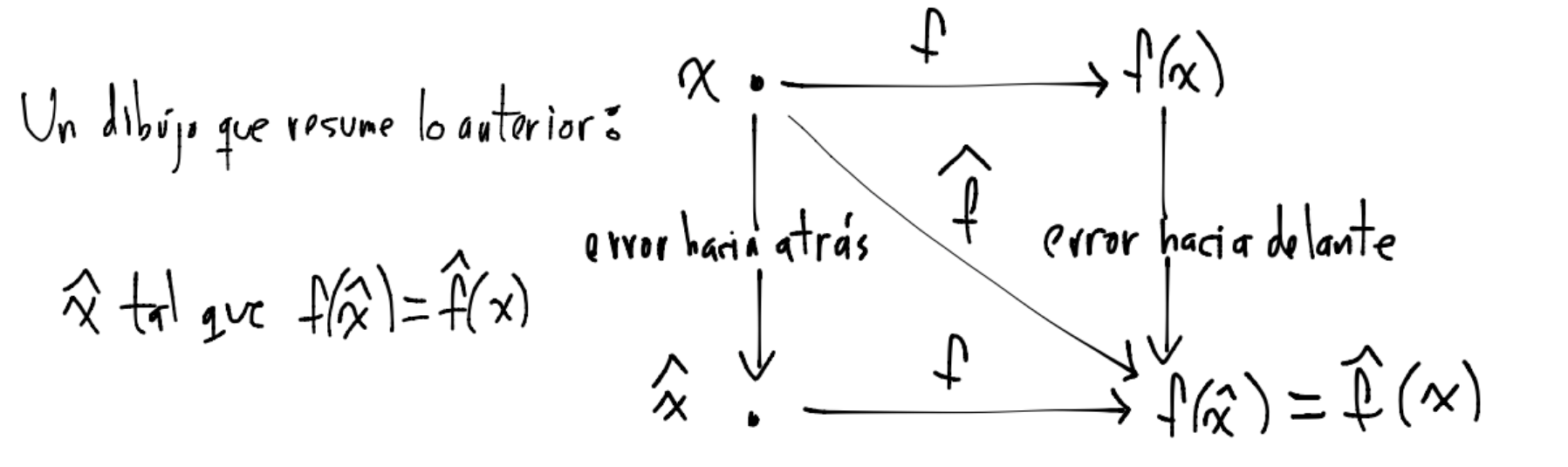
En resumen, algunas características de un método estable numéricamente respecto al redondeo son:
Variaciones “pequeñas” en las entradas del método generan variaciones “pequeñas” en la solución del problema.
No amplifican errores de redondeo en los cálculos involucrados.
Resuelven problemas “cercanos” para entradas ligeramente modificadas.
Observación
La estabilidad numérica que se revisó en esta sección hace referencia a los errores por redondeo de la aritmética y representación de los números en el sistema de punto flotante. Tal uso no debe confundirse con la estabilidad numérica en el tema de ecuaciones diferenciales, ver Stability_in_numerical_differential_equations.
Número de condición de una matriz#
En el curso trabajaremos con algoritmos matriciales que son numéricamente estables (o estables hacia atrás) ante errores por redondeo, sin embargo la exactitud que obtengamos con tales algoritmos dependerán de qué tan bien (o mal) condicionado esté el problema. En el caso de matrices la condición de un problema puede ser cuantificada con el número de condición de la matriz del problema. Aunque haciendo uso de definiciones como la pseudoinversa de una matriz es posible definir el número de condición para una matriz en general rectangular \(A \in \mathbb{R}^{m\times n}\), en esta primera definición consideramos matrices cuadradas no singulares \(A \in \mathbb{R}^{n\times n}\):
Observación
Obsérvese que la norma anterior es una norma matricial y cond\((\cdot)\) puede calcularse para diferentes normas matriciales. Ver Normas vectoriales y matriciales para definición de norma y propiedades.
Comentario
Para el número de condición de una matriz también se utiliza la letra kappa: \(\kappa(A) = ||A||||A^{-1}||\).
¿Por qué se utiliza la expresión \(||A|| ||A^{-1}||\) para definir el número de condición de una matriz?#
Esta pregunta tiene que ver con el hecho que tal expresión aparece frecuentemente en problemas típicos de matrices. Para lo anterior considérese los siguientes problemas \(f\):
1.Sean \(A \in \mathbb{R}^{n\times n}\) no singular, \(x \in \mathbb{R}^n\) y \(f\) el problema de realizar la multiplicación \(Ax\) para \(x\) fijo, esto es: \(f: \mathbb{R}^n \rightarrow \mathbb{R}^n\) dada por \(f(x) = Ax\). Considérese una perturbación en \(x: \hat{x} = x + \Delta x\), entonces:
Para este problema tenemos:
Si las normas matriciales utilizadas en el número de condición son consistentes (ver Normas vectoriales y matriciales para definición de norma y propiedades) entonces:
y se tiene:
2.Sean \(f: \mathbb{R}^n \rightarrow \mathbb{R}, A \in \mathbb{R}^{n\times n}\) no singular. Considérese el problema de calcular \(f(b) = A^{-1}b\) para \(b \in \mathbb{R}^n\) fijo y la perturbación \(\hat{b} = b + \Delta b\) entonces bajo las suposiciones del ejemplo anterior:
Si las normas matriciales utilizadas en el número de condición son consistentes (ver Normas vectoriales y matriciales para definición de norma y propiedades) entonces:
3.Sean \(f: \mathbb{R}^{n\times n} \rightarrow \mathbb{R}^n, A \in \mathbb{R}^{n\times n}\) no singular \(b \in \mathbb{R}^n\) fijo. Considérese el problema de calcular la solución \(x\) del sistema \(Az=b\), esto es, calcular: \(x = f(A) = A^{-1}b.\) Además, considérese la perturbación \(\hat{A} = A + \Delta A\) en el sistema \(Az = b\). Se tiene:
donde: \(\hat{x} = x + \Delta x\) (si se perturba \(A\) entonces se perturba también \(x\)).
De la ecuación anterior como \(\hat{x} = \hat{A}^{-1}b\) se tiene:
Donde en esta última ecuación se supuso que \(\Delta A \Delta x \approx 0\) y de aquí:
Entonces se tiene que la condición del problema \(f\): calcular la solución de sistema de ecuaciones lineales \(Az=b\) con \(A\) no singular ante perturbaciones en \(A\) es:
¿Qué está midiendo el número de condición de una matriz respecto a un sistema de ecuaciones lineales?#
El número de condición de una matriz mide la sensibilidad de la solución de un sistema de ecuaciones lineales ante perturbaciones en los datos de entrada (en la matriz del sistema \(A\) o en el lado derecho \(b\)). Si pequeños cambios en los datos de entrada generan grandes cambios en la solución tenemos un sistema mal condicionado. Si pequeños cambios en los datos de entrada generan pequeños cambios en la solución tenemos un sistema bien condicionado. Lo anterior puede apreciarse con los siguientes ejemplos y gráficas:
import numpy as np
import matplotlib.pyplot as plt
import scipy
import pprint
np.set_printoptions(precision=3, suppress=True)
1.Resolver los siguientes sistemas:
print('inciso a')
A = np.array([[1, 2], [1.1, 2]])
b = np.array([10,10.4])
print('matriz A:')
pprint.pprint(A)
print('lado derecho b:')
pprint.pprint(b)
inciso a
matriz A:
array([[1. , 2. ],
[1.1, 2. ]])
lado derecho b:
array([10. , 10.4])
x=np.linalg.solve(A,b)
print('solución x:')
pprint.pprint(x)
solución x:
array([4., 3.])
x=np.arange(0,10,.5)
recta1 = lambda x: 1/2.0*(10-1*x)
recta2 = lambda x: 1/2.0*(10.4-1.1*x)
plt.plot(x,recta1(x),'o-',x,recta2(x),'^-')
plt.title('Sistema mal condicionado')
plt.legend(('x1+2x2=10','1.1x1+2x2=10.4'))
plt.grid(True)
plt.show()

Observación
Obsérvese que las dos rectas anteriores tienen una inclinación (pendiente) similar por lo que no se ve claramente el punto en el que intersectan.
print('inciso b')
A = np.array([[1.05, 2], [1.1, 2]])
b = np.array([10,10.4])
print('matriz A ligeramente modificada:')
pprint.pprint(A)
print('lado derecho b:')
pprint.pprint(b)
inciso b
matriz A ligeramente modificada:
array([[1.05, 2. ],
[1.1 , 2. ]])
lado derecho b:
array([10. , 10.4])
x=np.linalg.solve(A,b)
print('solución x:')
pprint.pprint(x)
solución x:
array([8. , 0.8])
x=np.arange(0,10,.5)
recta1 = lambda x: 1/2.0*(10-1.05*x)
recta2 = lambda x: 1/2.0*(10.4-1.1*x)
plt.plot(x,recta1(x),'o-',x,recta2(x),'^-')
plt.title('Sistema mal condicionado')
plt.legend(('1.05x1+2x2=10','1.1x1+2x2=10.4'))
plt.grid(True)
plt.show()

Observación
Al modificar un poco las entradas de la matriz \(A\) la solución del sistema cambia drásticamente.
Comentario
Otra forma de describir a un sistema mal condicionado es que un amplio rango de valores en un SPF satisfacen tal sistema de forma aproximada.
2.Resolver los siguientes sistemas:
print('inciso a')
A = np.array([[.03, 58.9], [5.31, -6.1]])
b = np.array([59.2,47])
print('matriz A:')
pprint.pprint(A)
print('lado derecho b:')
pprint.pprint(b)
inciso a
matriz A:
array([[ 0.03, 58.9 ],
[ 5.31, -6.1 ]])
lado derecho b:
array([59.2, 47. ])
x=np.linalg.solve(A,b)
print('solución x:')
pprint.pprint(x)
solución x:
array([10., 1.])
x=np.arange(4,14,.5)
recta1 = lambda x: 1/58.9*(59.2-.03*x)
recta2 = lambda x: 1/6.1*(5.31*x-47)
plt.plot(x,recta1(x),'o-',x,recta2(x),'^-')
plt.title('Sistema bien condicionado')
plt.legend(('.03x1+58.9x2=59.2','5.31x1-6.1x2=47'))
plt.grid(True)
plt.show()

Observación
Obsérvese que la solución del sistema de ecuaciones (intersección entre las dos rectas) está claramente definido.
print('inciso b')
A = np.array([[.03, 58.9], [5.31, -6.05]])
b = np.array([59.2,47])
print('matriz A ligeramente modificada:')
pprint.pprint(A)
print('lado derecho b:')
pprint.pprint(b)
inciso b
matriz A ligeramente modificada:
array([[ 0.03, 58.9 ],
[ 5.31, -6.05]])
lado derecho b:
array([59.2, 47. ])
x=np.linalg.solve(A,b)
print('solución x:')
pprint.pprint(x)
solución x:
array([9.991, 1. ])
x=np.arange(4,14,.5)
recta1 = lambda x: 1/58.9*(59.2-.03*x)
recta2 = lambda x: 1/6.05*(5.31*x-47)
plt.plot(x,recta1(x),'o-',x,recta2(x),'^-')
plt.title('Sistema bien condicionado')
plt.legend(('.03x1+58.9x2=59.2','5.31x1-6.05x2=47'))
plt.grid(True)
plt.show()

Observación
Al modificar un poco las entradas de la matriz \(A\) la solución no cambia mucho.
Comentarios
1.¿Por qué nos interesa considerar perturbaciones en los datos de entrada? -> recuérdese que los números reales se representan en la máquina mediante el sistema de punto flotante (SPF), entonces al ingresar datos a la máquina tenemos perturbaciones y por tanto errores de redondeo. Ver nota: Sistema de punto flotante.
2.Las matrices anteriores tienen número de condición distinto:
print('matriz del ejemplo 1')
A = np.array([[1, 2], [1.1, 2]])
pprint.pprint(A)
matriz del ejemplo 1
array([[1. , 2. ],
[1.1, 2. ]])
print(np.linalg.cond(A))
51.030403839186725
print('matriz del ejemplo 2')
A = np.array([[.03, 58.9], [5.31, -6.1]])
pprint.pprint(A)
matriz del ejemplo 2
array([[ 0.03, 58.9 ],
[ 5.31, -6.1 ]])
print(np.linalg.cond(A))
11.205557604869346
Comentario
Las matrices del ejemplo \(1\) y \(2\) son medianamente condicionadas. Una matriz se dice bien condicionada si cond\((A)\) es cercano a \(1\).
Algunas propiedades del número de condición de una matriz#
Si \(A \in \mathbb{R}^{n\times n}\) es no singular entonces:
esto es, una matriz mal condicionada (número de condición grande) se le puede aproximar muy bien por una matriz singular. Sin embargo, el mal condicionamiento no necesariamente se relaciona con singularidad. Una matriz singular es mal condicionada pero una matriz mal condicionada no necesariamente es singular. Considérese por ejemplo la matriz de Hilbert:
from scipy.linalg import hilbert
print(hilbert(4))
[[1. 0.5 0.333 0.25 ]
[0.5 0.333 0.25 0.2 ]
[0.333 0.25 0.2 0.167]
[0.25 0.2 0.167 0.143]]
print(np.linalg.cond(hilbert(4)))
15513.738738928929
la cual es una matriz mal condicionada pero es no singular:
print(np.linalg.inv(hilbert(4))@hilbert(4))
[[ 1. -0. -0. -0.]
[ 0. 1. 0. 0.]
[-0. -0. 1. -0.]
[ 0. 0. 0. 1.]]
y otro ejemplo de una matriz singular:
print('matriz singular')
A = np.array([[1, 2], [1, 2]])
pprint.pprint(A)
matriz singular
array([[1, 2],
[1, 2]])
print(np.linalg.inv(A))
---------------------------------------------------------------------------
LinAlgError Traceback (most recent call last)
<ipython-input-30-91b18e07fae9> in <module>
----> 1 print(np.linalg.inv(A))
<__array_function__ internals> in inv(*args, **kwargs)
~/.local/lib/python3.7/site-packages/numpy/linalg/linalg.py in inv(a)
544 signature = 'D->D' if isComplexType(t) else 'd->d'
545 extobj = get_linalg_error_extobj(_raise_linalgerror_singular)
--> 546 ainv = _umath_linalg.inv(a, signature=signature, extobj=extobj)
547 return wrap(ainv.astype(result_t, copy=False))
548
~/.local/lib/python3.7/site-packages/numpy/linalg/linalg.py in _raise_linalgerror_singular(err, flag)
86
87 def _raise_linalgerror_singular(err, flag):
---> 88 raise LinAlgError("Singular matrix")
89
90 def _raise_linalgerror_nonposdef(err, flag):
LinAlgError: Singular matrix
print(np.linalg.cond(A))
inf
Para las normas matriciales inducidas se tiene:
cond\((A)\geq 1, \forall A \in \mathbb{R}^{n\times n}\).
cond\((\gamma A) = \text{cond}(A), \forall \gamma \in \mathbb{R}-\{0\}, \forall A \in \mathbb{R}^{n\times n}\).
cond\(_2(A) = ||A||_2||A^{-1}||_2 = \frac{\sigma_{\max}}{\sigma_{\min}}, \sigma_{\min} \neq 0\).
En el problema: resolver \(Ax = b\) se cumple:
donde: \(x^*\) es solución de \(Ax=b\) y \(\hat{x}\) es solución aproximada que se obtiene por algún método numérico (por ejemplo factorización LU). \(\frac{||\Delta A||}{||A||}, \frac{||\Delta b||}{||b||}\) son los errores relativos en las entradas de \(A\) y \(b\) respectivamente.
Comentario
La desigualdad anterior se puede interpretar como sigue: si sólo tenemos perturbaciones en \(A\) de modo que se tienen errores por redondeo del orden de \(10^{-k}\) y por lo tanto \(k\) dígitos de precisión en \(A\) y cond\((A)\) es del orden de \(10^c\) entonces \(\text{ErrRel}(\hat{x})\) puede llegar a tener errores de redondeo de a lo más del orden de \(10^{c-k}\) y por tanto \(k-c\) dígitos de precisión:
Supongamos que \(x^*\) es solución del sistema \(Ax=b\) y obtenemos \(\hat{x}\) por algún método numérico (por ejemplo factorización LU) entonces ¿qué condiciones garantizan que \(||x^*-\hat{x}||\) sea cercano a cero (del orden de \(\epsilon_{maq}= 10^{-16}\)), ¿de qué depende esto?
Definición
Para responder las preguntas anteriores definimos el residual de \(Ax=b\) como
con \(\hat{x}\) aproximación a \(x^*\) obtenida por algún método numérico. Asimismo, el residual relativo a la norma de \(b\) como:
Observación
Típicamente \(x^*\) (solución exacta) es desconocida y por ello no podríamos calcular \(||x^*-\hat{x}||\), sin embargo sí podemos calcular el residual relativo a la norma de \(b\): \(\frac{||r||}{||b||}\). ¿Se cumple que \(\frac{||r||}{||b||}\) pequeño implica \(\text{ErrRel}(\hat{x})\) pequeño? El siguiente resultado nos ayuda a responder esta y las preguntas anteriores.
Sea \(A \in \mathbb{R}^{n\times n}\) no singular, \(x^*\) solución de \(Ax=b\), \(\hat{x}\) aproximación a \(x^*\), entonces para las normas matriciales inducidas se cumple:
Por la desigualdad anterior, si \(\text{cond}(A) \approx 1\) entonces \(\frac{||r||}{||b||}\) es una buena estimación de \(\text{ErrRel}(\hat{x}) = \frac{||x^*-\hat{x}||}{||x^*||}\) por lo que si el residual relativo es pequeño entonces \(\hat{x}\) es una buena estimación de \(x^*\) (si la precisión y exactitud definida es aceptable para la aplicación o problema en cuestión). Si \(\text{cond}(A)\) es grande no podemos decir nada acerca de \(\text{ErrRel}(\hat{x})\) ni de \(\hat{x}\).
Ejemplos#
Para los siguientes ejemplos supóngase que \(x^*\) y \(\hat{x}\) son soluciones del inciso a) y b) respectivamente. Considérese como \(b\) el del sistema del inciso a) y aplíquese el resultado anterior.
1.Resolver:
print('inciso a')
A_1 = np.array([[1, 1], [10.05, 10]])
b_1 = np.array([2,21])
print('matriz A_1:')
pprint.pprint(A_1)
print('lado derecho b_1:')
pprint.pprint(b_1)
inciso a
matriz A_1:
array([[ 1. , 1. ],
[10.05, 10. ]])
lado derecho b_1:
array([ 2, 21])
x_est=np.linalg.solve(A_1,b_1)
print('solución x_est:')
pprint.pprint(x_est)
solución x_est:
array([ 20., -18.])
print('inciso b')
A_2 = np.array([[1, 1], [10.1, 10]])
b_2 = np.array([2,21])
print('matriz A_2:')
pprint.pprint(A_2)
print('lado derecho b_2:')
pprint.pprint(b_2)
inciso b
matriz A_2:
array([[ 1. , 1. ],
[10.1, 10. ]])
lado derecho b_2:
array([ 2, 21])
x_hat=np.linalg.solve(A_2,b_2)
print('solución x_hat:')
pprint.pprint(x_hat)
solución x_hat:
array([10., -8.])
print('residual relativo:')
r_rel = np.linalg.norm(A_1@x_hat-b_1)/np.linalg.norm(b_1)
print(r_rel)
residual relativo:
0.02370227315699886
print('error relativo:')
err_rel = np.linalg.norm(x_hat-x_est)/np.linalg.norm(x_est)
pprint.pprint(err_rel)
error relativo:
0.5255883312276278
no tenemos una buena estimación del error relativo a partir del residual relativo pues:
print(np.linalg.cond(A_1))
4060.0497536998155
De acuerdo a la cota del resultado el error relativo se encuentra en el intervalo:
print((r_rel*1/np.linalg.cond(A_1), r_rel*np.linalg.cond(A_1)))
(5.837926773040061e-06, 96.23240829319897)
2.Resolver:
print('inciso a')
A_1 = np.array([[4.1, 2.8], [9.7, 6.6]])
b_1 = np.array([4.1,9.7])
print('matriz A_1:')
pprint.pprint(A_1)
print('lado derecho b_1:')
pprint.pprint(b_1)
inciso a
matriz A_1:
array([[4.1, 2.8],
[9.7, 6.6]])
lado derecho b_1:
array([4.1, 9.7])
x_est=np.linalg.solve(A_1,b_1)
print('solución x_est:')
pprint.pprint(x_est)
solución x_est:
array([1., 0.])
print('inciso b')
A_2 = np.array([[4.1, 2.8], [9.7, 6.6]])
b_2 = np.array([4.11,9.7])
print('matriz A_2:')
pprint.pprint(A_2)
print('lado derecho b_2:')
pprint.pprint(b_2)
inciso b
matriz A_2:
array([[4.1, 2.8],
[9.7, 6.6]])
lado derecho b_2:
array([4.11, 9.7 ])
x_hat=np.linalg.solve(A_2,b_2)
print('solución x_hat:')
pprint.pprint(x_hat)
solución x_hat:
array([0.34, 0.97])
print('residual relativo:')
r_rel = np.linalg.norm(A_1@x_hat-b_1)/np.linalg.norm(b_1)
print(r_rel)
residual relativo:
0.0009495858335005704
print('error relativo:')
err_rel = np.linalg.norm(x_hat-x_est)/np.linalg.norm(x_est)
pprint.pprint(err_rel)
error relativo:
1.1732433677631406
no tenemos una buena estimación del error relativo a partir del residual relativo pues:
print(np.linalg.cond(A_1))
1622.9993838565106
print((r_rel*1/np.linalg.cond(A_1), r_rel*np.linalg.cond(A_1)))
(5.850808342540463e-07, 1.5411772226902969)
3.Resolver:
print('inciso a')
A_1 = np.array([[3.9, 11.6], [12.8, 2.9]])
b_1 = np.array([5.5,9.7])
print('matriz A_1:')
pprint.pprint(A_1)
print('lado derecho b_1:')
pprint.pprint(b_1)
inciso a
matriz A_1:
array([[ 3.9, 11.6],
[12.8, 2.9]])
lado derecho b_1:
array([5.5, 9.7])
x_est=np.linalg.solve(A_1,b_1)
print('solución x_est:')
pprint.pprint(x_est)
solución x_est:
array([0.704, 0.237])
print('inciso b')
A_2 = np.array([[3.95, 11.6], [12.8, 2.9]])
b_2 = np.array([5.5,9.7])
print('matriz A_2:')
pprint.pprint(A_2)
print('lado derecho b_2:')
pprint.pprint(b_2)
inciso b
matriz A_2:
array([[ 3.95, 11.6 ],
[12.8 , 2.9 ]])
lado derecho b_2:
array([5.5, 9.7])
x_hat=np.linalg.solve(A_2,b_2)
print('solución x_hat:')
pprint.pprint(x_hat)
solución x_hat:
array([0.705, 0.234])
print('residual relativo:')
r_rel = np.linalg.norm(A_1@x_hat-b_1)/np.linalg.norm(b_1)
print(r_rel)
residual relativo:
0.0031601448781200417
print('error relativo:')
err_rel = np.linalg.norm(x_hat-x_est)/np.linalg.norm(x_est)
pprint.pprint(err_rel)
error relativo:
0.004537910940159858
sí tenemos una buena estimación del error relativo a partir del residual relativo pues:
print(np.linalg.cond(A_1))
1.7884565161384884
print((r_rel*1/np.linalg.cond(A_1), r_rel*np.linalg.cond(A_1)))
(0.0017669676895154308, 0.005651781699215458)
4.Utilizando \(\theta=\frac{\pi}{3}\)
theta_1=math.pi/3
print((math.cos(theta_1),math.sin(theta_1)))
(0.5000000000000001, 0.8660254037844386)
theta_2 = math.pi/3 + .00005
print(theta_2)
1.0472475511965977
print((math.cos(theta_2),math.sin(theta_2)))
(0.49995669810482884, 0.8660504027018965)
Resolver:
print('inciso a')
A_1 = np.array([[math.cos(theta_1), -math.sin(theta_1)], [math.sin(theta_1), math.cos(theta_1)]])
b_1 = np.array([-1.5,2.4])
print('matriz A_1:')
pprint.pprint(A_1)
print('lado derecho b_1:')
pprint.pprint(b_1)
inciso a
matriz A_1:
array([[ 0.5 , -0.866],
[ 0.866, 0.5 ]])
lado derecho b_1:
array([-1.5, 2.4])
x_est=np.linalg.solve(A_1,b_1)
print('solución x_est:')
pprint.pprint(x_est)
solución x_est:
array([1.328, 2.499])
print('inciso b')
A_2 = np.array([[math.cos(theta_2), -math.sin(theta_2)], [math.sin(theta_2), math.cos(theta_2)]])
b_2 = np.array([-1.5,2.4])
print('matriz A_2:')
pprint.pprint(A_2)
print('lado derecho b_2:')
pprint.pprint(b_2)
inciso b
matriz A_2:
array([[ 0.5 , -0.866],
[ 0.866, 0.5 ]])
lado derecho b_2:
array([-1.5, 2.4])
x_hat=np.linalg.solve(A_2,b_2)
print('solución x_hat:')
pprint.pprint(x_hat)
solución x_hat:
array([1.329, 2.499])
print('residual relativo:')
r_rel = np.linalg.norm(A_1@x_hat-b_1)/np.linalg.norm(b_1)
print("{:0.10e}".format(r_rel))
residual relativo:
4.9999999995e-05
print('error relativo:')
err_rel = np.linalg.norm(x_hat-x_est)/np.linalg.norm(x_est)
print("{:0.10e}".format(err_rel))
error relativo:
4.9999999995e-05
sí tenemos una buena estimación del error relativo a partir del residual relativo pues:
print(np.linalg.cond(A_1))
1.0
print(("{:0.10e}".format(r_rel*1/np.linalg.cond(A_1)),
"{:0.10e}".format(r_rel*np.linalg.cond(A_1))))
('4.9999999995e-05', '4.9999999995e-05')
print('inciso c')
A_2 = np.array([[math.cos(theta_2), -math.sin(theta_2)], [math.sin(theta_2), math.cos(theta_2)]])
b_2 = np.array([-1.7,2.4])
print('matriz A_2:')
pprint.pprint(A_2)
print('lado derecho b_2:')
pprint.pprint(b_2)
inciso c
matriz A_2:
array([[ 0.5 , -0.866],
[ 0.866, 0.5 ]])
lado derecho b_2:
array([-1.7, 2.4])
x_hat=np.linalg.solve(A_2,b_2)
print('solución x_hat:')
pprint.pprint(x_hat)
solución x_hat:
array([1.229, 2.672])
print('residual relativo:')
r_rel = np.linalg.norm(A_1@x_hat-b_1)/np.linalg.norm(b_1)
print("{:0.14e}".format(r_rel))
residual relativo:
7.06241310531940e-02
print('error relativo:')
err_rel = np.linalg.norm(x_hat-x_est)/np.linalg.norm(x_est)
print("{:0.14e}".format(err_rel))
error relativo:
7.06241310531940e-02
sí tenemos una buena estimación del error relativo a partir del residual relativo pues:
print(np.linalg.cond(A_1))
1.0
print(("{:0.14e}".format(r_rel*1/np.linalg.cond(A_1)),
"{:0.14e}".format(r_rel*np.linalg.cond(A_1))))
('7.06241310531940e-02', '7.06241310531940e-02')
Así, \(\text{cond}(A)\) nos da una calidad (mediante \(\frac{||r||}{||b||}\)) de la solución \(\hat{x}\) en el problema inicial (resolver \(Ax=b\)) obtenida por algún método numérico respecto a la solución \(x^*\) de \(Ax=b\).
Observación
El ejercicio anterior (en el que se define el ángulo \(\theta\)) utiliza matrices de rotación que son matrices ortogonales. Las matrices ortogonales tienen número de condición igual a \(1\) bajo las normas inducidas.
Obsérvese que la condición del problema inicial (resolver \(Ax=b\)) no depende del método númerico que se elige para resolverlo.
Ejercicio:
Utilizando lenguajes de programación proponer sistemas de ecuaciones lineales con distinto número de condición, perturbar matriz del sistema o lado derecho (o ambos) y revisar números de condición y residuales relativos de acuerdo a la cota:
Verificar que si el número de condición del sistema es pequeño entonces el residual relativo estima bien al error relativo.
Número de condición de una matriz \(A \in \mathbb{R}^{m\times n}\)#
Para este caso se utiliza la pseudoinversa de \(A\) definida a partir de la descomposición en valores singulares compacta (compact SVD, ver Factorizaciones matriciales SVD, Cholesky, QR) y denotada como \(A^{\dagger}\):
donde: \(\Sigma ^{\dagger}\) es la matriz transpuesta de \(\Sigma\) y tiene entradas \(\sigma_i^{+}:\)
\(\forall i=1,\dots, r\) con \(r=rank(A)\).
Comentarios y propiedades
\(A^{\dagger}\) se le conoce como pseudoinversa de \(Moore-Penrose\).
Si \(rank(A)=n\) entonces \(A^{\dagger} = (A^TA)^{-1}A^T\), si \(rank(A)=m\), \(A^\dagger = A^T(AA^T)^{-1}\), si \(A\in \mathbb{R}^{n\times n}\) no singular, entonces \(A^\dagger=A^{-1}\).
Con \(A^\dagger\) se define \(\text{cond}(A)\) para \(A \in \mathbb{R}^{m\times n}\):
de hecho, se tiene:
Ejercicios
Resuelve los ejercicios y preguntas de la nota.
Preguntas de comprehensión
1)¿Qué factores influyen en la falta de exactitud de un cálculo?
2)Si f es un problema mal condicionado, ¿a qué nos referimos? Da ejemplos de problemas bien y mal condicionados.
3)Si f es un problema que resolvemos con un algoritmo g, ¿qué significa:
a. que g sea estable?
b. que g sea estable hacia atrás?
c. que g sea inestable?
4)¿Qué ventaja(s) se tiene(n) al calcular un error hacia atrás vs calcular un error hacia delante?
Referencias
L. Trefethen, D. Bau, Numerical linear algebra, SIAM, 1997.
G. H. Golub, C. F. Van Loan,Matrix Computations. John Hopkins University Press, 2013

